Q:给出一个只包含0和1的二维矩阵,找出最大的全部元素都是1的长方形区域,返回该区域的面积。
A:
这个题感觉蛮巧妙的。
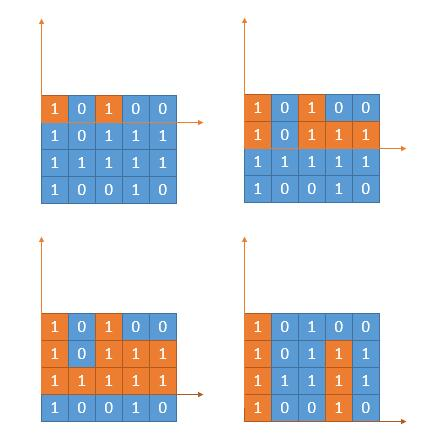
如果这个点为‘1’,先计算当前行的最大宽度,这说明最大宽度左边的都是保证可以是矩形的。然后往上看,用最小的宽度和当前的高度计算最大的矩形。
看图:
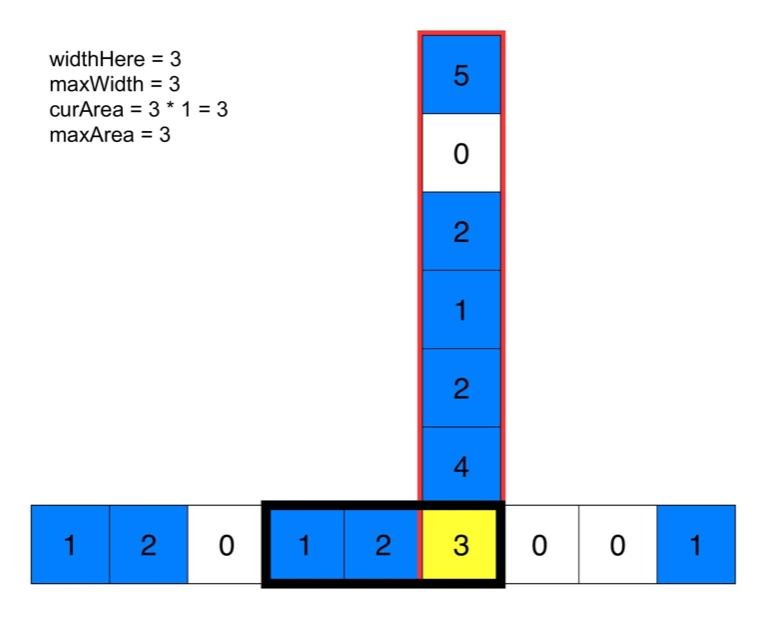
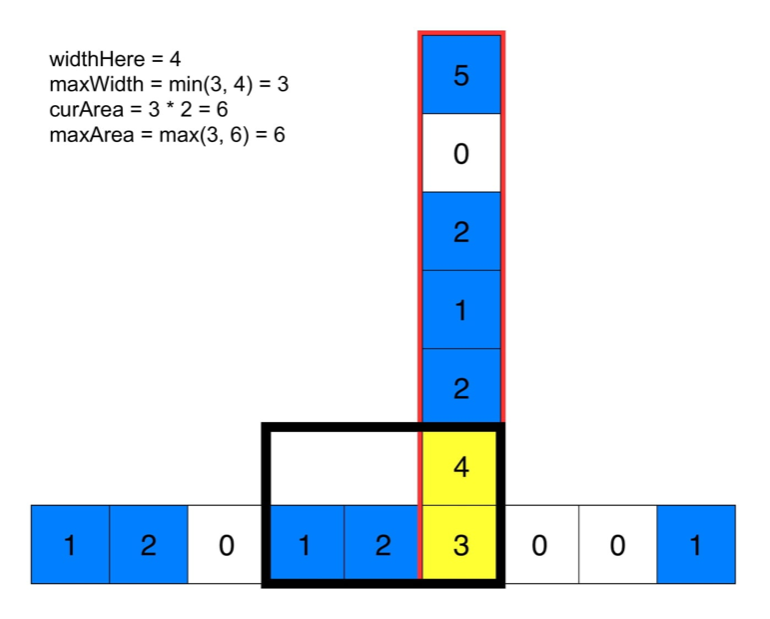

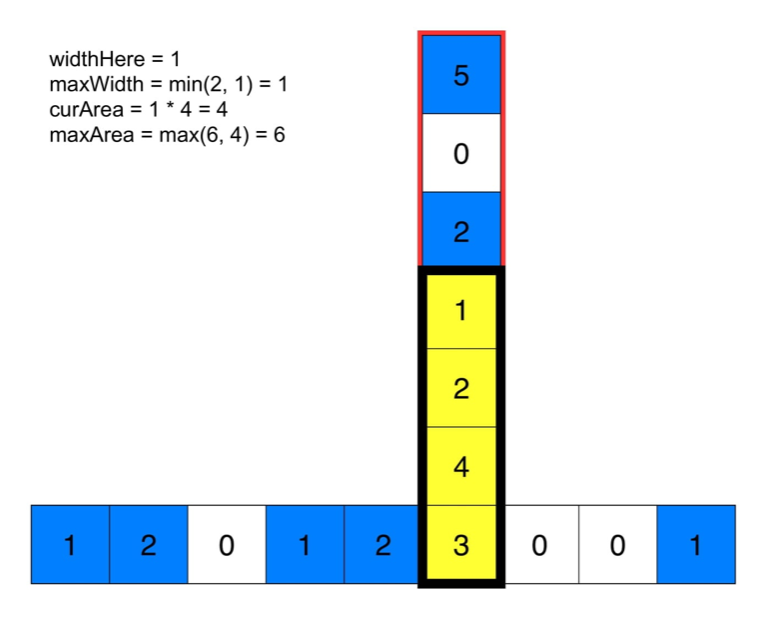


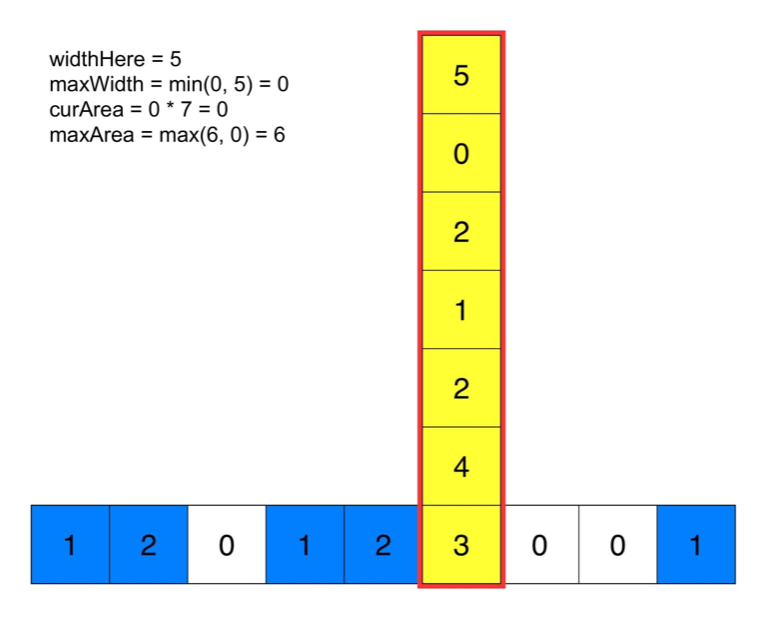
代码:
public int maximalRectangle(char[][] matrix) {
if (matrix.length == 0)
return 0;
int maxArea = 0;
int[][] dp = new int[matrix.length][matrix[0].length];
for (int i = 0; i < matrix.length; i++) {
for (int j = 0; j < matrix[0].length; j++) {
if (matrix[i][j] == '1') {
//先计算最大宽度
if (j == 0) {
dp[i][j] = 1;
} else {
dp[i][j] = dp[i][j - 1] + 1;
}
int width = dp[i][j];
for (int k = i; k >= 0; k--) {
width = Math.min(width, dp[k][j]);
maxArea = Math.max(maxArea, width * (i - k + 1));
}
}
}
}
return maxArea;
}
同理,高度也可以这么做。
另一种就是参考计算直方图中最大矩形的面积
算法有了,就是求出每一层的 heights[] 然后传给上一题的函数就可以了。
代码:
public int maximalRectangle(char[][] matrix) {
if (matrix.length == 0) {
return 0;
}
int maxArea = 0;
int[] dp = new int[matrix[0].length];
for (int i = 0; i < matrix.length; i++) {
for (int j = 0; j < matrix[0].length; j++) {
if (matrix[i][j] == '1') {
dp[j] = dp[j] + 1;
} else {
dp[j] = 0;
}
}
int area = maxRec(dp);
maxArea = Math.max(maxArea, area);
}
return maxArea;
}
private int maxRec(int[] heights) {
Stack<Integer> stack = new Stack < > ();
stack.push(-1);
int maxarea = 0;
for (int i = 0; i < heights.length; ++i) {
while (stack.peek() != -1 && heights[stack.peek()] >= heights[i])
maxarea = Math.max(maxarea, heights[stack.pop()] * (i - stack.peek() - 1));
stack.push(i);
}
while (stack.peek() != -1)
maxarea = Math.max(maxarea, heights[stack.pop()] * (heights.length - stack.peek() -1));
return maxarea;
}