刷了 5 个 2400~2600 题了,还真就第一个遇到不会做的题,而且还是个 2400。看来我思维水平为
线性对数做法
先讲一个大部分人用的线性对数做法。
注意到,每个 city 显然是由相邻两个 station 共同贡献的。那么显然,如果确定了这 (2n) 个贡献中的一个,那么就可以贪心地推出来其他 (2n-1) 个,然后判断是否可行。
我们设第一个是 (?+x),那么推出来的结果大概是
| 第一一一一一一一一一一一一一一一一列 | 第二二二二二二二二二二二二二二二二列 |
|---|---|
| (?) | (x) |
| (b_1-x) | (M(a_2-(b_1-x))) |
| (b_2-M(a_2-(b_1-x))) | (M(a_3-(b_2-M(a_2-(b_1-x))))) |
| (cdots) | (cdots) |
其中 (M(x)=max(0,x))。其中左一列就是当前 (b) 最多能给它贡献多少了,不考虑超过了 (a_i)。最后会循环到左上角,发现左上角的式子是最长的。
注意到,左边一列任意一个如果 (<0),就说明它上一行右边用的超过当前 (b) 了,也就是当前 (b) 不够用了,那肯定是不行的。如果都够用的话,还需要考虑到头来 (a_i) 能不能被第一行两个数的和所 (geq)。于是有解也就当且仅当能找到 (xgeq 0) 满足这两个条件。
然后我们想到,总不能枚举这个 (x) 吧,它可是关于值域的。那么二分?我证不出来它有单调性。但是注意到,(x) 合法所要满足的两个条件分别关于 (x) 满足单调性:
- 容易发现,(x) 增加一,那么左边一列全部都减少 (0sim 1),右边一列都增加 (0sim 1)。那么 (x) 越大,左边就越可能挂掉;(x) 越小,左边就越会活得好好的。所以说这样可以二分出 (x) 的一个上界;
- 又因为 (x) 增加一是铁定增加一的,而此时左上角有可能增加一,有可能不动。那么长期增加下来,第一行的和只会不减,于是 (x) 越大,第二个条件就越容易满足。所以可以二分出 (x) 的一个下界。
于是看下界是否 (leq) 上界即可。
线性做法
会讲两个线性做法。这都是我在学校和路上苦思冥想的结果啊,精通时事的人应该看到了我一边拿草稿本一边走路(
刚开始做的时候用的就是下面的其一,只不过我有东西没考虑到,所以最终还是看题解了/ll
其一是继续在刚刚的做法的列表格的基础之上做。我们考虑分别探索两个条件的充要条件:
-
(forall Nin[1,n],b_N-M(a_N-cdots)geq0)。移项得到 (M(a_N-cdots)leq b_N)。此时这个 (M) 非常好去,注意到若里面 (<0),泽肯定成立,去掉 (M) 也肯定成立,所以无伤大雅;若里面 (geq 0),则去不去 (M) 值一样。于是可以直接去掉 (M),得到 (a_N-cdotsleq b_N),即 (cdotsgeq a_N-b_N)。于是可以(近似的)归纳到 (b_{N-1}-M(a_{N-1}-cdots)geq a_N-b_N)。那么是否还可以像上面那样想当然地直接得到 (cdotsgeq a_N-b_N+a_{N-1}-b_{N-1}) 呢?nope。
注意到到 (M(a_{N-1}-cdots)leq b_{N-1}-a_N+b_N) 这一步,这时候右边不一定 (geq0)(这就是我一开始的思路,但是没想到这一个问题,所以就 WA 了)。如果右边 (<0),此时左边显然 (geq),不等式不可能成立;否则依然可以照上面分析,归纳下去。于是我们多了一系列条件:归纳的过程中,(M) 左边的那串式子必须 (geq0)。
于是我们得到:(forall Nin[1,n],forall lin(1,n],sumlimits_{i=l}^Nb_i-sumlimits_{i=l+1}^Na_igeq 0),并且 (x) 满足 (forall Nin[1,n],xleqsumlimits_{i=1}^Nb_i-sumlimits_{i=2}^Na_i)。
-
(b_n-M(a_n-cdots)+xgeq a_i)。这就相当于上面的不等式的右边从 (0) 变成了 (a_i-x)。类似上面分析 (M)、归纳,我们可以得到 (forall lin(1,n],sumlimits_{i=l}^nb_i-sumlimits_{i=l+1}^na_i-a_1+xgeq 0Leftrightarrow xgeq sumlimits_{i=l+1}^na_i+a_1-sumlimits_{i=1}^nb_i)。然后最后一步得到 (xleq sumlimits_{i=1}^nb_i-sumlimits_{i=1}^na_i+x),(x) 直接消掉得到了一个不关于 (x) 的条件。
就把上面得到的不关于 (x) 的条件直接判,关于的发现有上界和下界,分别取 (min) 和 (max),最后看 (x) 是否有解,别忘了 (xgeq0)。至于说有平方级个条件,那没关系,前缀和拆一拆递推一下即可。
其二。
其实做什么图论建模(比如网络流)做多了的人,看到这题都会感觉要建图。比如差分约束或者网络流。网络流其实是可以的,zqynb,但我不会。下面讲的是差分约束的方法。
依然考虑 (2n) 个贡献,我们设它们为 (x_{i,1/2})。显然可以列出一堆关于它们的不等式:
但是这里是 (+) 号,差分约束个锤子啊?不急,不难发现前两条里面都是一个 (1) 一个 (2),于是我们可以用 (-x_{i,2}) 来搞,这样就可以差分约束了。
然后判有解性即可。显然不等式的个数是线性的,那么直接 SPFA 是平方的,会爆炸。但注意到这个建图还是蛮有规律的,考虑能不能用一些巧妙的方法判负环的存在性,就好似以前做过的某个巧妙求最短路的题一样。
把 (n=4) 的图画出来,还挺 good-looking 的(
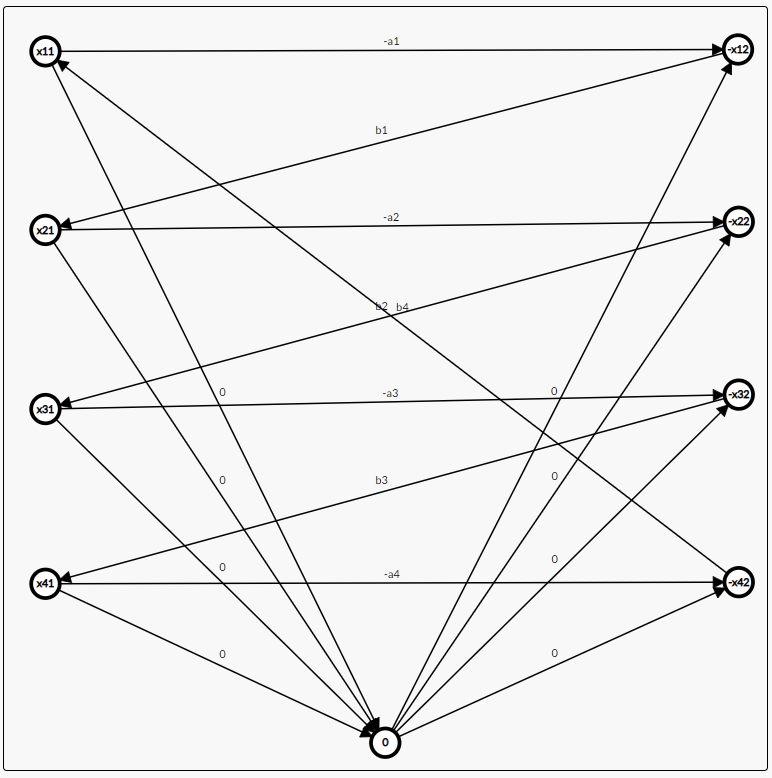
注意到,所有的环分为含 (0) 的环和不含 (0) 的环,我们只需要判断每个环都是非负环即可:
-
含 (0)。那么 (0) 两边只能是左边是正,右边是负,也就是正的每个到负的每个的路径要非负,即:
- 对于 (u>v) 有 (sumlimits_{i=v}^{u-1}b_i-sumlimits_{i=v+1}^{u-1}a_igeq 0);
- 对于 (uleq v) 有 (sb-sumlimits_{i=u}^{v-1}b_i-sa+sumlimits_{i=u}^va_igeq 0),其中 (sa,sb) 分别为 (a,b) 的和。
看似有平方级个条件,但按照上一个方法拆前缀和递推即可;
-
不含 (0)。那显然只有一个环:(sb-sa)。
然后这两种线性方法的条件集合按理说应该是等价的,看上去也很等价。但我不想想了。