贝叶斯定理(英语:Bayes' theorem)
是概率论中的一个定理,它跟随机变量的条件概率以及边缘概率分布有关。在有些关于概率的解释中,贝叶斯定理(贝叶斯公式)能够告知我们如何利用新证据修改已有的看法。这个名称来自于托马斯·贝叶斯。
通常,事件A在事件B(发生)的条件下的概率,与事件B在事件A(发生)的条件下的概率是不一样的。然而,这两者是有确定的关系的,贝叶斯定理就是这种关系的陈述。贝叶斯公式的一个用途在于通过已知的三个概率函数推出第四个。
贝叶斯定理是关于随机事件A和B的条件概率的一则定理。
- P(A|B)=P(A) P(B|A){P(B)
其中P(A|B)是指在事件B发生的情况下事件A发生的概率。
在贝叶斯定理中,每个名词都有约定俗成的名称:
- P(A|B)是已知B发生后A的条件概率,也由于得自B的取值而被称作A的后验概率。
- P(A)是A的先验概率(或边缘概率)。之所以称为"先验"是因为它不考虑任何B方面的因素。
- P(B|A)是已知A发生后B的条件概率,也由于得自A的取值而被称作B的后验概率。
- P(B)是B的先验概率或边缘概率。
按这些术语,贝叶斯定理可表述为:
- 后验概率 = (似然性*先验概率)/标准化常量
也就是说,后验概率与先验概率和相似度的乘积成正比。
另外,比例P(B|A)/P(B)也有时被称作标准似然度(standardised likelihood),贝叶斯定理可表述为:
后验概率 = 标准似然度*先验概率
二、贝叶斯定理(详细)---------转载之http://www.ruanyifeng.com/blog/2011/08/bayesian_inference_part_one.html
要理解贝叶斯推断,必须先理解贝叶斯定理。后者实际上就是计算"条件概率"的公式。
所谓"条件概率"(Conditional probability),就是指在事件B发生的情况下,事件A发生的概率,用P(A|B)来表示。
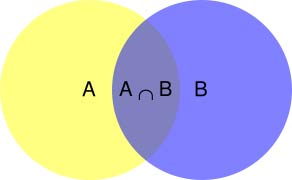
根据文氏图,可以很清楚地看到在事件B发生的情况下,事件A发生的概率就是P(A∩B)除以P(B)。
因此,
同理可得,
所以,
即
这就是条件概率的计算公式。
三、全概率公式
由于后面要用到,所以除了条件概率以外,这里还要推导全概率公式。
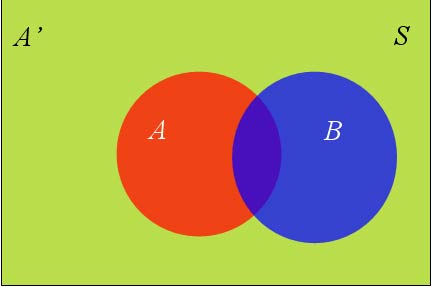
假定样本空间S,是两个事件A与A'的和。

上图中,红色部分是事件A,绿色部分是事件A',它们共同构成了样本空间S。
在这种情况下,事件B可以划分成两个部分。
即
在上一节的推导当中,我们已知
所以,
这就是全概率公式。它的含义是,如果A和A'构成样本空间的一个划分,那么事件B的概率,就等于A和A'的概率分别乘以B对这两个事件的条件概率之和。
将这个公式代入上一节的条件概率公式,就得到了条件概率的另一种写法:
四、贝叶斯推断的含义
对条件概率公式进行变形,可以得到如下形式:
我们把P(A)称为"先验概率"(Prior probability),即在B事件发生之前,我们对A事件概率的一个判断。P(A|B)称为"后验概率"(Posterior probability),即在B事件发生之后,我们对A事件概率的重新评估。P(B|A)/P(B)称为"可能性函数"(Likelyhood),这是一个调整因子,使得预估概率更接近真实概率。
所以,条件概率可以理解成下面的式子:
后验概率 = 先验概率 x 调整因子
这就是贝叶斯推断的含义。我们先预估一个"先验概率",然后加入实验结果,看这个实验到底是增强还是削弱了"先验概率",由此得到更接近事实的"后验概率"。
在这里,如果"可能性函数"P(B|A)/P(B)>1,意味着"先验概率"被增强,事件A的发生的可能性变大;如果"可能性函数"=1,意味着B事件无助于判断事件A的可能性;如果"可能性函数"<1,意味着"先验概率"被削弱,事件A的可能性变小。
五、【例子】水果糖问题
为了加深对贝叶斯推断的理解,我们看两个例子。
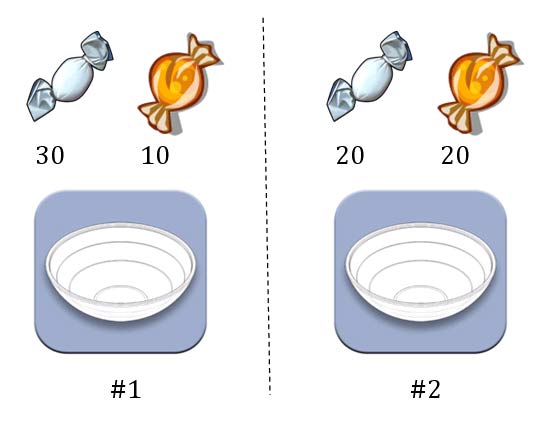
第一个例子。两个一模一样的碗,一号碗有30颗水果糖和10颗巧克力糖,二号碗有水果糖和巧克力糖各20颗。现在随机选择一个碗,从中摸出一颗糖,发现是水果糖。请问这颗水果糖来自一号碗的概率有多大?
我们假定,H1表示一号碗,H2表示二号碗。由于这两个碗是一样的,所以P(H1)=P(H2),也就是说,在取出水果糖之前,这两个碗被选中的概率相同。因此,P(H1)=0.5,我们把这个概率就叫做"先验概率",即没有做实验之前,来自一号碗的概率是0.5。
再假定,E表示水果糖,所以问题就变成了在已知E的情况下,来自一号碗的概率有多大,即求P(H1|E)。我们把这个概率叫做"后验概率",即在E事件发生之后,对P(H1)的修正。
根据条件概率公式,得到
已知,P(H1)等于0.5,P(E|H1)为一号碗中取出水果糖的概率,等于0.75,那么求出P(E)就可以得到答案。根据全概率公式,
所以,
将数字代入原方程,得到
这表明,来自一号碗的概率是0.6。也就是说,取出水果糖之后,H1事件的可能性得到了增强。
六、【例子】假阳性问题
第二个例子是一个医学的常见问题,与现实生活关系紧密。

已知某种疾病的发病率是0.001,即1000人中会有1个人得病。现有一种试剂可以检验患者是否得病,它的准确率是0.99,即在患者确实得病的情况下,它有99%的可能呈现阳性。它的误报率是5%,即在患者没有得病的情况下,它有5%的可能呈现阳性。现有一个病人的检验结果为阳性,请问他确实得病的可能性有多大?
假定A事件表示得病,那么P(A)为0.001。这就是"先验概率",即没有做试验之前,我们预计的发病率。再假定B事件表示阳性,那么要计算的就是P(A|B)。这就是"后验概率",即做了试验以后,对发病率的估计。
根据条件概率公式,
用全概率公式改写分母,
将数字代入,
我们得到了一个惊人的结果,P(A|B)约等于0.019。也就是说,即使检验呈现阳性,病人得病的概率,也只是从0.1%增加到了2%左右。这就是所谓的"假阳性",即阳性结果完全不足以说明病人得病。
为什么会这样?为什么这种检验的准确率高达99%,但是可信度却不到2%?答案是与它的误报率太高有关。
