都说矩阵其实就是线性映射,你明白不?反正一开始我是不明白的;
线性映射用矩阵表示:(很好明白的)
有两个线性空间,分别为V1与V2, V1的一组基表示为
,V2的一组基表示为
;(注意哦,维度可以不一样啊,反正就是线性空间啊),
1, 现在呢,有一个从V1到V2的映射F, 它可以把V1中的一组基都映射到线性空间V2中去,所以有:
用矩阵可以表示为:
2,现在我们把在V1中有一个向量A,经过映射F变为了向量B,用公式表示为:
所以呢,我们可以把矩阵看作是线性变换或线性映射;
矩阵的特征值与特征向量:
应该说是线性映射的特征值与特征向量,因为映射可以用矩阵表示,所以也可以说是矩阵的特征值与特征向量,当线性映射所在的表示为(100;010;001)的形式时,它们的特征值也特征向量相同;
1,用线性映射表示:
在空间V中的一个线性映射F,若在空间V的存在一个向量
,满足下面:
2,用矩阵表示:
把上面的公式改改,把矩阵A表示映射,用坐标
来表示向量
,可以得到:
因为向量
映射后结果为
,所以,映射前后的线性空间是没有变化的,所以映射前后可以用同一组基
表示,所以有:
最后得到:
特征值与特征向量的几个定理 :
需要强调地是:对于一个N重根的特征值,它的特征向量的基础解系的个数是小于或等于N的,即上面说的几何重复度小于或等于代数重复度; 对于不是重根的特征值,只能对应一个特征向量的基础解系;(基础解系就是特征向量组成的线性空间的基啊);
举两个例子:
上面两个矩阵中,左边的矩阵的特征值为二重根1,它的特向量的基础解系只有一个:(1,0); 右边矩阵的特征值为二重根1,它的特征向量的基础解系有两个:(1,0)和(0,1);
上面的矩阵中,左边的矩阵的特征值为1和2,特征值1对应的特征向量的基础解系为(1,0,0); 特征值2对应的特征向量的基础解系只有一个:(1,1,0);
右边的矩阵的特征值为1和2, 特征值1对应的特征向量的基础解系为(1,0,0); 特征值2对应的特征向量的基础解系有两个,分别为:(1,0,1)和(0,1,-1);
(说明:在重跟的情况下,选择的基础解系不是唯一的,不同的基础解系是可以互相表示的, 在不同基础解系下表示的线性空间是唯一的;)
看看特征向量到底是什么?
对于一个映射,特征向量才是本质有用的,特征值的作用不大。一个特征值对应了一个特征向量族(因为可以乘以一个系数,可以它的个数是无穷的),而一个特征向量只能对应一个特征值;
在一个映射中,不同的特征值对应的特征向量组成的线性空间中的向量的方向(负也表示不变)不会发生变化,只是scale变了,缩放倍数即为特征值;
例如:对于不是非重根的特征值的特征向量只有一个,它组成的线性空间是一维的,在映射过程中,在它上面的向量的方向不变; 对于多个重根的特征值的特征向量可以有多个,所以它们组成的线性空间是多维的,在这个线性空间中的向量在映射过程中的方向也是不变的;
![clip_image002[6] clip_image002[6]](https://images2017.cnblogs.com/blog/961754/201707/961754-20170726230229468-1211652311.png)
![clip_image002[8] clip_image002[8]](https://images2017.cnblogs.com/blog/961754/201707/961754-20170726230230125-914235049.png)
![clip_image002[38] clip_image002[38]](https://images2017.cnblogs.com/blog/961754/201707/961754-20170726230231234-85648505.png)
![clip_image002[12] clip_image002[12]](https://images2017.cnblogs.com/blog/961754/201707/961754-20170726230232218-523670720.png)
![clip_image002[16] clip_image002[16]](https://images2017.cnblogs.com/blog/961754/201707/961754-20170726230233140-13741700.png)
![clip_image002[18] clip_image002[18]](https://images2017.cnblogs.com/blog/961754/201707/961754-20170726230233875-1782773410.png)
![clip_image002[20] clip_image002[20]](https://images2017.cnblogs.com/blog/961754/201707/961754-20170726230234437-377108966.png)
![clip_image002[18] clip_image002[18]](https://images2017.cnblogs.com/blog/961754/201707/961754-20170726230234968-510776273.png)
![clip_image002[23] clip_image002[23]](https://images2017.cnblogs.com/blog/961754/201707/961754-20170726230235515-270219081.png)
![clip_image002[41] clip_image002[41]](https://images2017.cnblogs.com/blog/961754/201707/961754-20170726230239890-1009391758.png)
![clip_image002[43] clip_image002[43]](https://images2017.cnblogs.com/blog/961754/201707/961754-20170726230240562-1501255926.png)
![clip_image002[50] clip_image002[50]](https://images2017.cnblogs.com/blog/961754/201707/961754-20170726230243296-1590182034.png)
![clip_image002[36] clip_image002[36]](https://images2017.cnblogs.com/blog/961754/201707/961754-20170726230243937-824060430.png)




![clip_image002[1] clip_image002[1]](https://images2017.cnblogs.com/blog/961754/201707/961754-20170727120113774-1742650110.png)
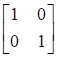
![clip_image002[3] clip_image002[3]](https://images2017.cnblogs.com/blog/961754/201707/961754-20170727120114977-1376949246.png)
![clip_image004[4] clip_image004[4]](https://images2017.cnblogs.com/blog/961754/201707/961754-20170727120117118-1697964169.png)