线性代数（新视角）

线性代数（新视角）

1）重新看待Ax=b

对于如下矩阵

 

行视图(凸优化中的超平面)

2x-y=1

x+y=5

 

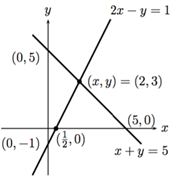
它的解是(x,y)=(2,3)

列视图（矩阵列的线性组合）

 

 

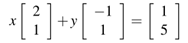
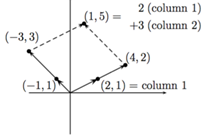
2）线性相关与线性无关

对于一个矩阵，使用一组非全为0的系数，如果任一列可以使用其他列线性表出，那么就称这组矩阵是线性相关的，否则非相关。

 

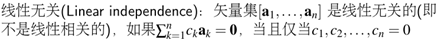
3）Span，基和子空间

 

对于下面一个问题，S表示为三维空间中的一个平面，如果任意一个线性无关的矩阵可以将S表示出来，那么这个矩阵就可以称为S的一组基。

 

4）四个基本的子空间

 

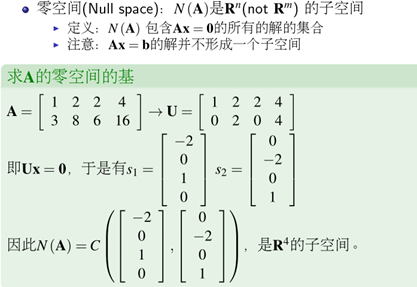
5）四个基本的子空间关系图

对于Ax=b, A的维度是m*n

（1）列空间和零空间，

对于Ax=b ，A的列构成的所有线性组合，构成了列空间，维度是r, 是Rⁿ空间中的一个子空间

Ax=0所有解的的集合构成了零空间，维度是n-r，是Rⁿ空间中的一个子空间，列空间和零空间构成了一个完整的Rⁿ空间

（2）行空间和左零空间

对于A^Tx=b, A的行构成的所有线性组合，构成了行空间，维度是r, 是R^m空间中的一个子空间

A^Ty=0所有解的的集合构成了左零空间，维度是m-r，是R^m空间中的一个子空间，行空间和左零空间构成了一个完整的R^m空间。

 

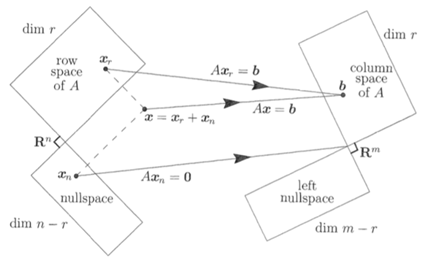
利用子空间重新看待线性方程组的解：