记得小学学数学的时候老师会说,偶数都能被二整出;各个位数和为3的倍数的数能被3整出,末尾是5的倍数的数能被5整除。
当时只是单纯的记下来了,用了这么多年也没觉得怎么样。
在无意间想到,这应该是有规律的,然后就做了下面这张表:
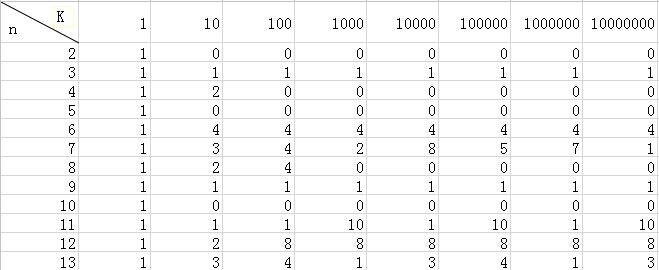
对于表中,K代表是十进制上每位的权值,这里值列举了这几个;N代表是整数(1除外,除1没意义)
从3来看:可以看到对于所有的权值来说,K÷3=X······1,从中可以看到所有的余数都为1。那么现在回想原来老师讲的,各个数位的和,其实就是各个数位上的值对于3的余数的和。也就等于把一个数字分解为各个数位的数值的和,这样的话只要余数的和为3的倍数那就一定会整除。
从上面的结论来看别的数值会发现,就是相同的道理。但是当数字超过10时,这么来看有显得不便了,因为余数的规律不同了,而且也没有必要记录这么多。
所以我们一般只教过,2,3,5。
对于其中的结论:(a%c+b%c)%c=(a+b)%c