二叉搜索树定义
二叉搜索树,又称为二叉排序树。Binary Search Tree,Binary Sort Tree,简写为BST。二叉排序树或为空树;或者是这样一棵二叉树,若左子树不空,则左子树上所有结点均小于根结点,若右子树不空,则右子树上所有结点均大于根结点,其左、右子树也是二叉排序树。
时间复杂度
二叉搜索树插入、删除、和搜索的时间是O(log(n))。
中序遍历BST可以得到一个关键字的有序序列,所以按排序顺序打印出所有节点时间复杂度为O(n)。如果中序遍历二叉排序树,将得到有序的关键字序列,这也是手工判别二叉排序树的方法之一。给定一个数,可以在O(log(n)) 时间内找出大小仅次于它的节点(方法为记住当前遍历过的最小差值和对应节点号,直至NULL)。
特性
在构建BST的过程中,新插入的结点一定是一个新添加的叶子节点,并且是查找不成功时查找路径上访问的最后一个节点的做孩子或者右孩子。构建二叉树的过程,就是对一个无序序列进行排序的过程。
查找算法
插入算法
删除算法
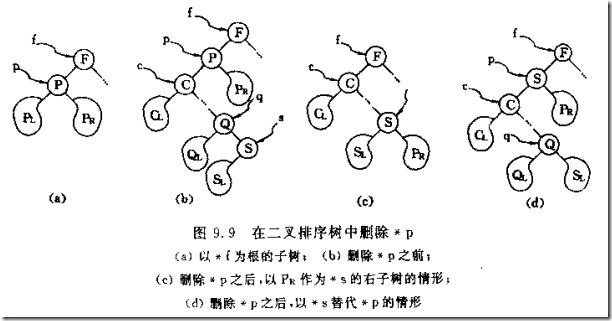
如下图所示,删除节点P时,如果P左右子树都非空,可以有两种方法将树重新调整为BST:
一,让以左孩子C为根的子树替代P的位置,将右孩子为根的子树Pr重新连接到P的直接前驱节点S,作为S的右子树(得到图c)。
二,让P的直接前驱节点S替换P,S的左子树连接到S的父节点作为右子树(得到图d)。
删除算法如下,