一.动态规划,通常用于求解最优化子结构问题和子问题重叠的情况
(1)最优子结构:问题的最优解由相关子问题的最优解组合而成,而这些子问题可以独立求解
(2)子问题重叠:不同的子问题具有公共的子子问题。比如:问题4 可以分出(3,2,1,0)四种子问题,但其中问题3和问题2都可以分出问题0和问题1,这就是公共的子子问题
算法描述:
1.刻画一个最优解的结构特征
最优子结构:问题的最优解由相关子问题的最优解组合而成,而这些子问题可以独立求解
(1)原问题涉及多个子问题,
(2)假定某种策略产生的子问题能可以得到最优解
(3)给定可获得的最优解的策略后,确定该策略会产生哪些子问题以及如何刻画子问题空间
(4)作为构成原问题最优解的组成部分,每个子问题的解就是它本身的最优解,而且这些子问题的解不互相影响
2.递归地定义最优解的值
(1)子问题的无关性:子问题相互之间不共享资源
(2)子问题的重叠性:两个子问题实际上是同一个子问题,只是作为不同问题的子问题出现而已
重叠子问题的求解:问题的递归算法会反复地求解相同的子问题,而不是一直生成新的子问题
3.计算最优解的值,通常采用自底向上的方法
自底向上法:恰当地定义子问题的规模,使任何子问题的求解都只依赖更小的子问题的求解,对子问题按规模从小到大求解并保存
4.利用计算出的信息构造一个最优解
原问题最优解一般是子问题最优解的和,外加选择子问题的策略
二:动态规划和分治法
1.相同:二者都要求原问题具有最优子结构性质,都是将原问题分成若干个子问题
2.不同:
(1)分治法:子问题之间相互独立,递归求解,合并子问题的解成为原问题的解
(2)动态规划:子问题具有重叠性,一般自底向上求解,最优解需要合理地构造
三.钢条切割
1.问题描述:已知不同长度的钢条价格不同,问给定一段钢条,怎样切割才能使价格收益最大?
2.简单分析:一般来说。长度为n英寸的钢条共有2**(n-1)中不同的切割方案(在距离钢条左端 i 英寸处,总可以选择切割或不切割两种情况)
3.一般求解:把规模n的问题分解成两段规模分别是 i 和 n-i 的子问题,接着求解这两段的最优切割收益,并在所有可能的两段切割方案中选取组合收益最大者,构成原问题最优解
4.更简单的递归求解:固定左边切下长度为 i 的一段,只对右边长度 n-i 的一段进行切割(递归求解)


1 #固定左边切割的i段,只对右边n-i进行切割(求解最优解) 2 def cut_rod(p, n): 3 if n == 0: 4 return 0 5 q = float("-inf") 6 for i in range(0, n): 7 q = max(q, p[i] + cut_rod(p, n - i - 1)) 8 return q 9 10 p = [1, 5, 8, 9, 10, 17, 17, 20, 24, 30] 11 for i in range(1, 11): 12 print("长度为", i, "的钢条的切割最大收益为:", end='') 13 print(cut_rod(p, i)) 14 ------------------------------------------------------------------- 15 长度为 1 的钢条的切割最大收益为:1 16 长度为 2 的钢条的切割最大收益为:5 17 长度为 3 的钢条的切割最大收益为:8 18 长度为 4 的钢条的切割最大收益为:10 19 长度为 5 的钢条的切割最大收益为:13 20 长度为 6 的钢条的切割最大收益为:17 21 长度为 7 的钢条的切割最大收益为:18 22 长度为 8 的钢条的切割最大收益为:22 23 长度为 9 的钢条的切割最大收益为:25 24 长度为 10 的钢条的切割最大收益为:30
5.动态规划:仔细安排求解顺序,对每个子问题只求解一次,并将结果保存下来。用空间来节省时间



1 #带备忘的自顶向下法 2 def memorized_cut_rod(p, n): 3 #p价格列表,n规模大小 4 r = []#每个子问题的解的列表,先初始化全为负无穷 5 for i in range(n): 6 r.append(float("-inf")) 7 return memorized_cut_rod_aux(p, n, r) 8 9 10 def memorized_cut_rod_aux(p, n, r): 11 #r[i]规模为i的最优切割收益 12 if r[n - 1] >= 0:#如果子问题的解在备忘录中存在,则直接返回 13 return r[n - 1] 14 if n == 0:#如果长度为0,则收益为0 15 q = 0 16 else: 17 q = float("-inf")#先初始化收益为 18 for i in range(0, n):#计算收益,取组合收益最大者,固定左边收益,递归求街右边最优解 19 q = max(q, p[i] + memorized_cut_rod_aux(p, n - i - 1, r)) 20 r[n - 1] = q#把收益保存到备忘录中 21 return q 22 23 print("动态规划方法:") 24 p=[1,5,8,9,10,17,17,20,24,30] 25 for i in range(1,11): 26 print("长度为",i,"的钢条的切割最大收益为:",end='') 27 print(memorized_cut_rod(p,i)) 28 ----------------------------------------------- 29 动态规划方法: 30 长度为 1 的钢条的切割最大收益为:1 31 长度为 2 的钢条的切割最大收益为:5 32 长度为 3 的钢条的切割最大收益为:8 33 长度为 4 的钢条的切割最大收益为:10 34 长度为 5 的钢条的切割最大收益为:13 35 长度为 6 的钢条的切割最大收益为:17 36 长度为 7 的钢条的切割最大收益为:18 37 长度为 8 的钢条的切割最大收益为:22 38 长度为 9 的钢条的切割最大收益为:25 39 长度为 10 的钢条的切割最大收益为:30


1 #自底向上 2 def bottom_up_cut_rod(p,n): 3 #p收益列表,n问题规模 4 r=[]#r子问题的解的列表 5 for i in range(n+1): 6 r.append(float("-inf")) 7 r[0]=0 8 for j in range(n):#升序求解规模为j的解 9 q=float("-inf") 10 for i in range(j+1): 11 q=max(q,p[i]+r[j-i]) 12 r[j+1]=q#把规模为j的子问题的最优解存入r[j+1] 13 return r[n] 14 15 p = [1, 5, 8, 9, 10, 17, 17, 20, 24, 30] 16 print("动态规划方法2:") 17 for i in range(1,11): 18 print("长度为",i,"的钢条的切割最大收益为:",end='') 19 print(bottom_up_cut_rod(p,i)) 20 ----------------------------------------------------------------- 21 动态规划方法2: 22 长度为 1 的钢条的切割最大收益为:1 23 长度为 2 的钢条的切割最大收益为:5 24 长度为 3 的钢条的切割最大收益为:8 25 长度为 4 的钢条的切割最大收益为:10 26 长度为 5 的钢条的切割最大收益为:13 27 长度为 6 的钢条的切割最大收益为:17 28 长度为 7 的钢条的切割最大收益为:18 29 长度为 8 的钢条的切割最大收益为:22 30 长度为 9 的钢条的切割最大收益为:25 31 长度为 10 的钢条的切割最大收益为:30




1 #每个子问题不仅保存最优收益值,还保存对应的切割方案 2 def extended_bottom_up_cut_rod(p,n): 3 r=[]#保存最优解 4 s=[]#保存最优解对应的第一段钢条的切割长度 5 for i in range(n+1): 6 r.append(float("-inf")) 7 s.append(float("-inf")) 8 r[0]=0 9 s[0]=0 10 #j+1表示钢条的长度,i+1表示第一段的长度 11 for j in range(n): 12 q=float("-inf") 13 for i in range(j+1): 14 if q<p[i]+r[j-i]: 15 q=p[i]+r[j-i] 16 s[j+1]=i+1 17 r[j+1]=q 18 return r,s 19 20 def print_cut_rod_solution(p,n): 21 #打印长度n的完整最优切割方案 22 (r,s)=extended_bottom_up_cut_rod(p,n) 23 while n>0: 24 print(s[n],' ',end='') 25 n=n-s[n] 26 print() 27 28 p = [1, 5, 8, 9, 10, 17, 17, 20, 24, 30] 29 for i in range(1,11): 30 print("长度为",i,"的钢条的切割最大收益的切割方案为:",end='') 31 print_cut_rod_solution(p,i) 32 ----------------------------------------------------------------------- 33 长度为 1 的钢条的切割最大收益的切割方案为:1 34 长度为 2 的钢条的切割最大收益的切割方案为:2 35 长度为 3 的钢条的切割最大收益的切割方案为:3 36 长度为 4 的钢条的切割最大收益的切割方案为:2 2 37 长度为 5 的钢条的切割最大收益的切割方案为:2 3 38 长度为 6 的钢条的切割最大收益的切割方案为:6 39 长度为 7 的钢条的切割最大收益的切割方案为:1 6 40 长度为 8 的钢条的切割最大收益的切割方案为:2 6 41 长度为 9 的钢条的切割最大收益的切割方案为:3 6 42 长度为 10 的钢条的切割最大收益的切割方案为:10
四.矩阵链
1.前提:(1)矩阵乘法满足结合律(2)两矩阵相乘时应具有相容性:前一个矩阵的列数等于后一个矩阵的行数
(3)A(10*100)A(100*5)A(5*50)的规模10*100*5次标量乘法,而A(10*100)【A(100*5)A(5*50)】的规模10*5*50次标量乘法,虽然结果一样,但计算速度不同
2.问题描述:多个A1A2...An矩阵相乘,试给出最快的相乘顺序,其中Ai的规模为pi-1*pi(4)完全括号化:单一矩阵,或者是两个完全括号化的矩阵乘积链的积,且已外加括号
3.一般分析:穷举显然不可取,对于一个n个矩阵的链,P(n)表示可供选择的括号化方案的数量,任意完全括号化矩阵可以表示成两个完全括号化的部分积相乘的形式,而两个部分积的划分点在第k个矩阵和第k+1个矩阵之间简而言之,一个矩阵链可以分成两个矩阵链相乘
4.动态规划求解:
(1)最优子结构:问题的最优解由相关子问题的最优解组合而成,而这些子问题可以独立求解
原问题分解:A[i]...A[j],假设它最优括号化方案的分割点在A[k],则把原问题分为两个子问题,A[i]...A[k]和A[k+1]...A[j],这两个子问题都可以独立求出他们的最优解
(组合)计算A[i]...A[j]的代价等于计算A[i]...A[k]和A[k+1]...A[j]的代价,再加上两者相乘的计算代价
(2)一个递归求解方案
假设最优分割点k是已知的,记m[i,j]表示计算矩阵A[i,j]的代价,矩阵A(i)的大小为p(i-1)*p(i),则由上得m[i,j]=m[i,k]+m[k+1,j]+p(i-1)p(k)p(j)
又k其实只有j-i中取值,则取其中使代价最大的k
(3)计算子问题最优解的值,对于A[1]...A[n]从底到上递归计算它的每个子问题的最优解,并保存

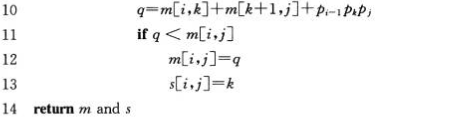
(4)构造原问题最优解,子问题最优解组合成原问题最优解


1 #计算子问题最优代价 2 def matrix_chain_order(p): 3 #p输入序列p(0)-p(n) 4 n = len(p) - 1#n矩阵链长度 5 m = [[0 for j in range(0, n + 1)] for i in range(0, n + 1)]#m矩阵保存每一个子问题的最优计算代价 6 s = [[0 for j in range(0, n + 1)] for i in range(0, n + 1)]#s矩阵记录最优值对应的分割点k 7 for l in range(2, n + 1): 8 for i in range(1, n - l + 2): 9 j = i + l - 1 10 m[i][j] = float("inf") 11 for k in range(i, j): 12 q = m[i][k] + m[k + 1][j] + p[i - 1] * p[k] * p[j] 13 if q < m[i][j]:#取对于[i,j]中每一个k,取达到最优值(最小值)的哪一个 14 m[i][j] = q 15 s[i][j] = k 16 return m, s 17 18 #构造最优解 19 def print_optimal_parens(s, i, j): 20 #s矩阵保存子问题最优解的矩阵 21 if i == j: 22 print("A", i, end='') 23 else: 24 print("(", end='') 25 print_optimal_parens(s, i, s[i][j]) 26 print_optimal_parens(s, s[i][j] + 1, j) 27 print(")", end='') 28 29 p = [30,35,15,5,10,20,25] 30 m, s = matrix_chain_order(p) 31 print(m) 32 print(s) 33 print_optimal_parens(s,1 , 6) 34 ----------------------------------------------------------------- 35 [[0, 0, 0, 0, 0, 0, 0], [0, 0, 15750, 7875, 9375, 11875, 15125], [0, 0, 0, 2625, 4375, 7125, 10500], [0, 0, 0, 0, 750, 2500, 5375], [0, 0, 0, 0, 0, 1000, 3500], [0, 0, 0, 0, 0, 0, 5000], [0, 0, 0, 0, 0, 0, 0]] 36 [[0, 0, 0, 0, 0, 0, 0], [0, 0, 1, 1, 3, 3, 3], [0, 0, 0, 2, 3, 3, 3], [0, 0, 0, 0, 3, 3, 3], [0, 0, 0, 0, 0, 4, 5], [0, 0, 0, 0, 0, 0, 5], [0, 0, 0, 0, 0, 0, 0]] 37 ((A 1(A 2A 3))((A 4A 5)A 6))
五.最长公共子序列(longest-common-subsequence)(LCS)
1.前提:(1)子序列:x是y的一个子序列:序列x包含序列y,而且y在x中的下标严格递增
(2)公共子序列:序列z既是序列x的子序列,又是序列y的子序列,则z为x和y的公共子序列
2.问题描述:求序列x和序列y的最长的公共子序列
3.动态规划求解:
(1)最优子结构特征:定义X的第i前缀为Xi=(x1...xi),两个序列的LCS包含两个序列的前缀的LSC

(2)一个递归解:定义c[i,j]表示Xi和Yj的LCS长度

(3)计算LCS的长度
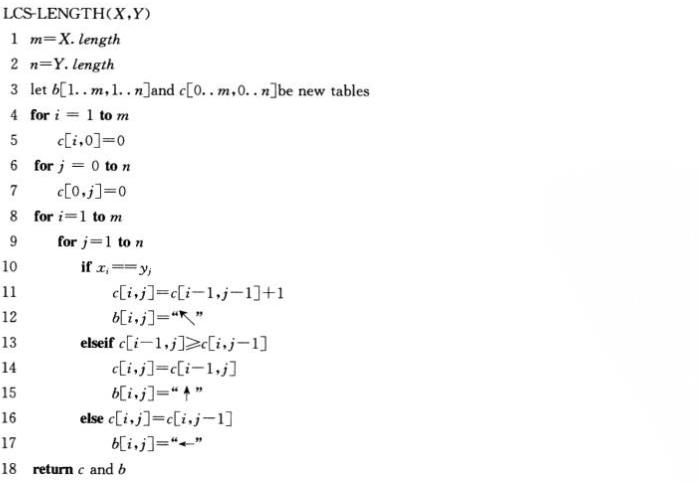
(4)构造LCS
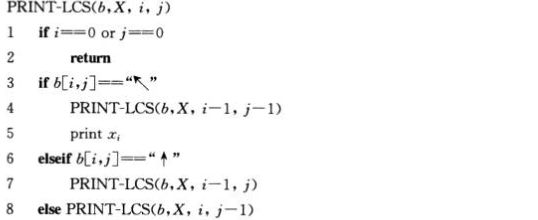

1 #计算LCS长度 2 def lcs_length(X, Y): 3 #LCS长度 4 m = len(X) 5 n = len(Y) 6 c = [[0 for j in range(n + 1)] for i in range(m + 1)]#c矩阵保存X和Y的LCS长度 7 b = [[" " for j in range(n + 1)] for i in range(m + 1)]#b保存子问题最优解 8 for i in range(1, m + 1): 9 for j in range(1, n + 1): 10 #计算每个i,j的最优解, 11 # 仅仅依赖于是否xi=yi以及c[i-1,j],c[i,j-1],c[i-1,j-1]的值,这些值都会在c[i,j]之间计算出来 12 if X[i - 1] == Y[j - 1]: 13 c[i][j] = c[i - 1][j - 1] + 1 14 b[i][j] = "向左上" 15 elif c[i - 1][j] >= c[i][j - 1]: 16 c[i][j] = c[i - 1][j] 17 b[i][j] = "向上" 18 else: 19 c[i][j] = c[i][j - 1] 20 b[i][j] = "向左" 21 return c, b 22 23 #构造LCS,根据LCS长度 24 def print_lcs(b, X, i, j): 25 if i == 0 or j == 0: 26 return 27 if b[i][j] == "向左上": 28 print_lcs(b, X, i - 1, j - 1) 29 print(X[i - 1], end='') 30 elif b[i][j] == "向上": 31 print_lcs(b, X, i - 1, j) 32 else: 33 print_lcs(b, X, i, j - 1) 34 35 X = ["A", "B", "C", "B", "D", "A", "B"] 36 Y = ["B", "D", "C", "A", "B", "A"] 37 c, b = lcs_length(X, Y) 38 for i in range(len(X) + 1): 39 for j in range(len(Y) + 1): 40 print(c[i][j], ' ', end='') 41 print() 42 for i in range(len(X) + 1): 43 for j in range(len(Y) + 1): 44 print(b[i][j], ' ', end='') 45 print() 46 print_lcs(b, X, len(X), len(Y)) 47 --------------------------------------------- 48 0 0 0 0 0 0 0 49 0 0 0 0 1 1 1 50 0 1 1 1 1 2 2 51 0 1 1 2 2 2 2 52 0 1 1 2 2 3 3 53 0 1 2 2 2 3 3 54 0 1 2 2 3 3 4 55 0 1 2 2 3 4 4 56 57 向上 向上 向上 向左上 向左 向左上 58 向左上 向左 向左 向上 向左上 向左 59 向上 向上 向左上 向左 向上 向上 60 向左上 向上 向上 向上 向左上 向左 61 向上 向左上 向上 向上 向上 向上 62 向上 向上 向上 向左上 向上 向左上 63 向左上 向上 向上 向上 向左上 向上 64 BCBA
六.最优二叉搜索树
1.背景:要在一堆数据中进行查找操作,把每条数据关联一个关键字,每条数据的搜索频率不同,有的频繁地查找,有的很少进行查找,把所有关键字(在关键字序列中的)和伪关键字(不在关键字序列中的)设计成二叉树的结构,从上到下表示查找顺序,要求频繁出现的关键字靠近树根
2.问题描述:对于一个给定的概率集合,我们希望构造一棵搜索代价最小的二叉搜索树
3.注意:二叉搜索树不一定是高度最矮的,而且,概率最高的关键字也不一定出现在二叉搜索树的根结点
4.动态规划求解:
(1)最优子结构特征
考虑一棵二叉搜索树的任意子树,关键字ki...kj和伪关键字d(i-1)...dj,如果它是一棵最优二叉搜索树的子树,那它必然也是最优的
(2)递归算法
子问题域:求解包含关键字ki...kj的最优二叉搜索树
求解:从ki...kj中选择一个根节点kr,构造ki...kr-1的左子树(最优二叉搜索树)和kr+1...kj的右子树(最优二叉搜索树)
(3)计算期望搜索代价




1 def optimal_bst(p, q, n): 2 #p关键字概率列表,q伪关键字概率列表,n输入规模 3 #e代价矩阵,w概率矩阵,root记录包含关键字ki...kj的子树的根 4 e = [[0 for j in range(n + 1)] for i in range(n + 2)] 5 w = [[0 for j in range(n + 1)] for i in range(n + 2)] 6 root = [[0 for j in range(n + 1)] for i in range(n + 1)] 7 for i in range(n + 2): 8 e[i][i - 1] = q[i - 1] 9 w[i][i - 1] = q[i - 1] 10 for l in range(1, n + 1): 11 for i in range(1, n - l + 2): 12 j = i + l - 1 13 e[i][j] = float("inf") 14 w[i][j] = w[i][j - 1] + p[j] + q[j] 15 for r in range(i, j + 1): 16 t = e[i][r - 1] + e[r + 1][j] + w[i][j] 17 if t < e[i][j]: 18 e[i][j] = t 19 root[i][j] = r 20 return e, root 21 22 23 24 p = [0, 0.15, 0.1, 0.05, 0.1, 0.2] 25 q = [0.05, 0.1, 0.05, 0.05, 0.05, 0.1] 26 e, root = optimal_bst(p, q, 5) 27 for i in range(5 + 2): 28 for j in range(5 + 1): 29 print(e[i][j], " ", end='') 30 print() 31 for i in range(5 + 1): 32 for j in range(5 + 1): 33 print(root[i][j], " ", end='') 34 print() 35 ----------------------------------------------------- 36 0 0 0 0 0 0.1 37 0.05 0.45000000000000007 0.9 1.25 1.75 2.75 38 0 0.1 0.4 0.7 1.2 2.0 39 0 0 0.05 0.25 0.6 1.2999999999999998 40 0 0 0 0.05 0.30000000000000004 0.9 41 0 0 0 0 0.05 0.5 42 0 0 0 0 0 0.1 43 0 0 0 0 0 0 44 0 1 1 2 2 2 45 0 0 2 2 2 4 46 0 0 0 3 4 5 47 0 0 0 0 4 5 48 0 0 0 0 0 5
