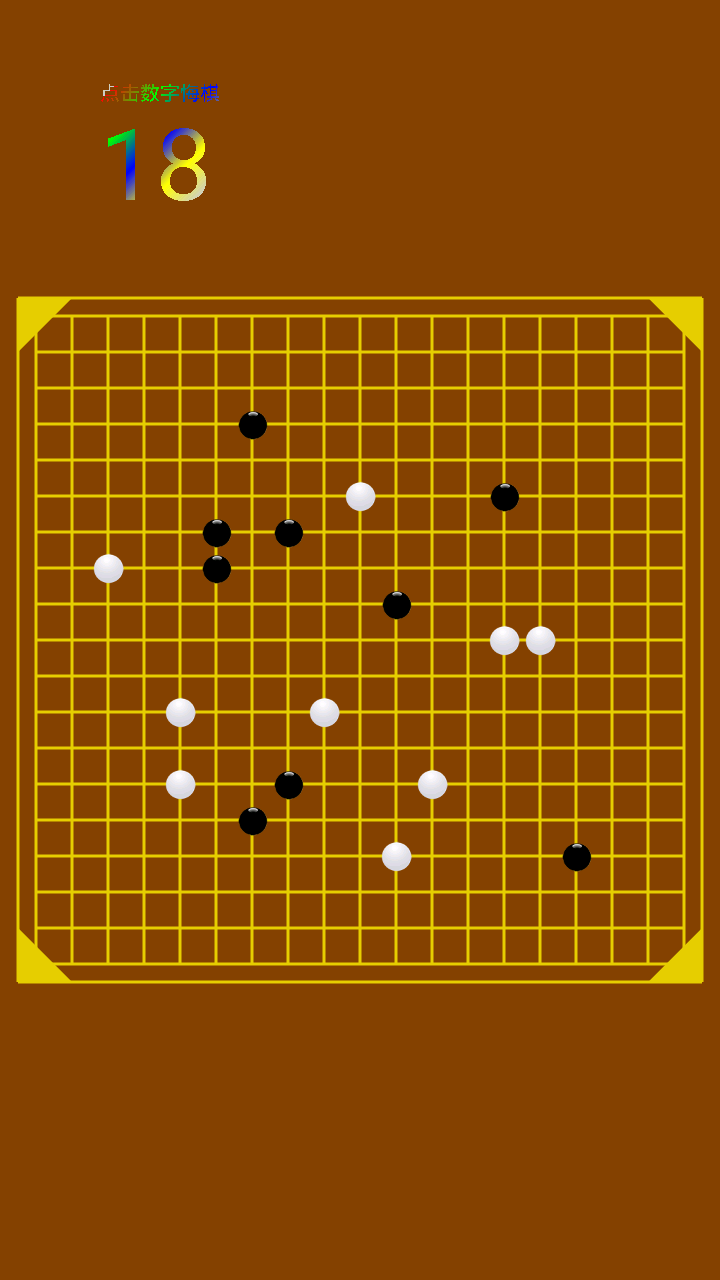
两天完成基本功能,再对其进行细节bug优化,本小白的思路。
思路:
1.用canvas绘制棋盘:得到手机的分辨率。棋盘大小为19*19。将手机宽屏分为21份,取中间19份为棋盘。上下空白位置为按钮功能。
如下:画出棋盘。

1 protected void onDraw(Canvas canvas,Paint paint) { 2 3 canvas.drawColor(Color.rgb(128,64,0)); 4 //canvas.drawColor(Color.WHITE); 5 w = chess_W/20;//平均分为21块 横坐标 6 h =scrren_h/2-chess_W/2; 7 for(int i =1; i<=19; i++ ){ //21分,画其中的地1份和第19份,0和20不画 8 canvas.drawLine(i*w,h+w,i*w,h+19*w, paint); 9 }//绘制直线 10 for(int i =1; i<=19;i++) 11 { 12 13 canvas.drawLine(w,h+i*w,19*w,h+i*w, paint); 14 } 15 paint.setStrokeWidth(3); 16 canvas.drawLine(w/2,h+w/2,w/2, h+19*w+w/2, paint); 17 canvas.drawLine(19*w+w/2,h+w/2,19*w+w/2,h+19*w+w/2, paint); 18 canvas.drawLine(w/2,h+w/2,19*w+w/2, h+w-w/2, paint); 19 canvas.drawLine(w/2,h+19*w+w/2,19*w+w/2, h+19*w+w/2, paint); 20 21 /* 22 * (w,h+w) (19*w,h+w) 23 * 24 * 25 * (w,h+19*w) (19*w,h+19*w) 26 * */ 27 28 //绘制四角 29 // 绘制这个三角形,你可以绘制任意多边形 30 paint.setColor(Color.rgb(227,207,0)); 31 Path path = new Path(); 32 path.moveTo(w/2,h+18*w);// 此点为多边形的起点 33 path.lineTo(w/2,h+19*w+w/2); 34 path.lineTo(2*w,h+19*w+w/2); 35 path.close(); // 使这些点构成封闭的多边形 36 canvas.drawPath(path, paint); 37 38 Path path1 = new Path(); 39 path1.moveTo(w/2,h+w/2);// 此点为多边形的起点 40 path1.lineTo(w/2,h+w+w); 41 path1.lineTo(2*w,h+w/2); 42 path1.close(); // 使这些点构成封闭的多边形 43 canvas.drawPath(path1, paint); 44 Path path2= new Path(); 45 path2.moveTo(19*w+w/2,h+w/2);// 此点为多边形的起点 46 path2.lineTo(19*w+w/2,h+2*w); 47 path2.lineTo(18*w,h+w/2); 48 path2.close(); // 使这些点构成封闭的多边形 49 canvas.drawPath(path2, paint); 50 Path path3 = new Path(); 51 path3.moveTo(19*w+w/2,h+19*w+w/2);// 此点为多边形的起点 52 path3.lineTo(18*w,h+19*w+w/2); 53 path3.lineTo(19*w+w/2,h+18*w); 54 path3.close(); // 使这些点构成封闭的多边形 55 canvas.drawPath(path3, paint); 56 }
2.在棋盘上落子:用canvas.bitmap。
需要注意的是:1.落子的地方以前没有被落子
2.落子的要保证落在棋盘的线上
3.落子要保证随心,不能与下棋者按下的棋点有偏差。
4.持黑先行,用步数控制应该下黑白棋。
5.采用一个二维数组存储数据,未落子为0,黑子为1,白子为2.
6.貌似canvas画图需要每次落子都要重新绘图,要从数组的提取数据依次绘图。可以自己设计算法,提高速度,比如根据步数,当发现棋子数量等于步数 后面就不用遍历了。最好不要全部遍历数组。
7.采用数组要注意数组越界问题。
8.边界问题!!!这个很重要。
落子落在棋线上和存储落子数据:

/判断落子 public float downx(float x,float y) { if (x > ChessDraw.w / 2 && x < ChessDraw.w * 19 + ChessDraw.w / 2) { if (y > ChessDraw.h + ChessDraw.w / 2 && y < ChessDraw.h + 19 * ChessDraw.w + ChessDraw.w / 2) { int kx = (int) (x / ChessDraw.w); int jx = (int) (x % ChessDraw.w); if (jx >= ChessDraw.w / 2) { //过了格子的一半 kx++; x = kx * ChessDraw.w; if(kx>20 || kx<=0) { //防止数组越界 x=-100; } } else{ //未过格子的一半 x = kx * ChessDraw.w; if(kx>20 || kx<=0) { //防止数组越界 x=-100; } } //获取落子的地点x chess_x=kx; } else { MySurfaceView.downQ = false; //不在棋盘,不允许落子 } } else { MySurfaceView.downQ = false; //不在棋盘,不允许落子 } return x; } //判断落子 public float downy(float x, float y) { if (x > ChessDraw.w / 2 && x < ChessDraw.w * 19 + ChessDraw.w / 2) { if (y > ChessDraw.h + ChessDraw.w / 2 && y < ChessDraw.h + 19 * ChessDraw.w + ChessDraw.w / 2) { //error int ky = (int) ((y - ChessDraw.w / 2 - ChessDraw.h) / ChessDraw.w); int jy = (int) ((y - ChessDraw.w / 2 - ChessDraw.h) % ChessDraw.w); if (jy >= ChessDraw.w / 2) { //如果过了格子的一般 ky++; y = ky * ChessDraw.w + ChessDraw.h ; if(ky>20 || ky<=0) { //防止数组越界 y=-100; } } else{//如果没有过格子的一半 y=ky * ChessDraw.w + ChessDraw.h; if(ky>20 || ky<=0) { //防止数组越界 y=-100; } } //获取落子的地点x chess_y=ky; } else { MySurfaceView.downQ = false; } } else { MySurfaceView.downQ = false; //不在棋盘,不允许落子 } return y; } public void downarr(int x, int y,int step){ if(step % 2 != 0) chess_arr[x][y]=MySurfaceView.BLACK_CHESS; else chess_arr[x][y]=MySurfaceView.WRITE_CHESS; }
3.胜利的判断,一共四个方向。对落子位子四个方向进行判断,如果一个方向累计成功五次以上即可。要注意数组坐标越界,可使用try catch,可优化算法。比如,前9步无需判断等,此处尚未优化,很暴力。

public ChessVictory(){ chessRule = new ChessRule(); } public void chessvictory(int x, int y) { int c =chessRule.chess_arr[x][y]; for (int i = 0; i < 4; i++) { //四个方向 linetrue2 = true; linetrue1 = true; victory_num=0; tx1=0; ty1=0; tx2=0; ty2=0; for (int k = 0; k < 5; k++) { try { if (i == 0 && victory == false) {//对Y轴判断 ty1++; int Ky1 = y+ty1; ty2--; int Ky2 = y+ty2; if (linetrue1 && (chessRule.chess_arr[x][Ky1] == c)) { victory_num++; } else { linetrue1 = false; } //y轴--判断,注意数组越界 if (linetrue2 && chessRule.chess_arr[x][Ky2] ==c) { victory_num++; } else { linetrue2 = false; } if (victory_num >= 4) { victory = true; } } //对x轴判断 if (i == 1 && victory == false) { tx1++; int Kx1 = x+tx1; tx2--; int Kx2 = x+tx2; if (linetrue1 && chessRule.chess_arr[Kx1][y] == c) { victory_num++; } else { linetrue1 = false; } //y轴--判断,注意数组越界 if (linetrue2 && chessRule.chess_arr[Kx2][y] ==c) { victory_num++; } else { linetrue2 = false; } if (victory_num >= 4) { victory = true; } } //斜对角判断 if (i == 2 && victory == false) { tx1++; int kx1 = x+tx1; tx2--; int kx2 = x+tx2; ty1++; int ky1 = y+ty1; ty2--; int ky2 = y+ty2; if (linetrue1 && chessRule.chess_arr[kx2][ky1] == c) { victory_num++; } else { linetrue1 = false; } //y轴--判断,注意数组越界 if (linetrue2 && chessRule.chess_arr[kx1][ky2] == c) { victory_num++; } else { linetrue2 = false; } if (victory_num >= 4) { victory = true; } } //斜对角判断 if (i == 3 && victory == false) { tx1++; int kx1 = x+tx1; tx2--; int kx2 = x+tx2; ty1++; int ky1 = y+ty1; ty2--; int ky2 = y+ty2; if (linetrue1 && chessRule.chess_arr[kx2][ky2] == c) { victory_num++; } else { linetrue1 = false; } //y轴--判断,注意数组越界 if (linetrue2 && chessRule.chess_arr[kx1][ky1] ==c) { victory_num++; } else { linetrue2 = false; } if (victory_num >= 4) { victory = true; } } } catch (Exception e) { } } }
4.悔棋问题:
若只允许悔棋一次,可以直接对存储数据的数组操作。
若允许多次,可以在new一个数组进行每一步的存储(貌似数组存储不太好,具体实现的时候要考虑),悔棋时从此数组提取位子,在存储数据的数组上修改。
若要保存、载入等等。均可以在上次new的数组上进行保存。这样可以实现打谱。每次下一子,重现对局(未实现,只是思路)。
5.细节优化,比如从游戏进入后台,再从后台打开要保存原来的位置。本以为很难,其实在完成的时候只不过一笔带过。以及其余优化。
6.对战和AI设计。。。。继续完成。
