【算法总结】二叉排序树
二叉排序树是一棵特殊的二叉树,它是一棵二叉树但同时满足如下条件:对于树上任意一个结点,其上的数值必大于等于其左子树上任意结点数值,必小于等于其右子树上任意结点的数值。
二叉排序树的存储方式与二叉树保持一致,我们更多的关注它独有的操作。
我们从二叉树的插入开始了解其建树方式,对二叉排序树插入数字 x:
1.若当前树为空,则 x 为其根结点。
2.若当前结点大于 x,则 x 插入其左子树;若当前结点小于 x,则 x 插入其右子树;若当前结点等于 x,则根据具体情况选择插入左右子树或者直接忽略。
以插入 4、2、6、1、3 为例,其二叉排序树变化情况如下图。
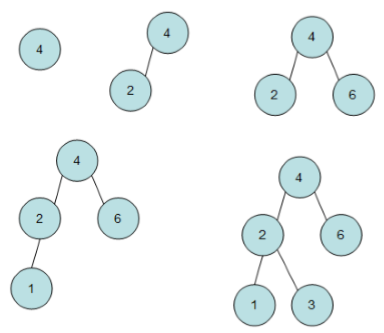
由于各个数字插入的顺序不同,所得到的二叉排序树的形态也很可能不同, 所以不同的插入顺序对二叉排序树的形态有重要的影响。但是,所有的二叉排序树都有一个共同的特点:若对二叉排序树进行中序遍历,那么其遍历结果必然是一个递增序列,这也是二叉排序树名字的来由,通过建立二叉排序树就能对原无序序列进行排序,并实现动态维护。
insert函数的返回值是Node指针这一点非常重要,因为要往前拱就必须“生长”左右子结点。
AC代码
#include<cstdio> #include<cstring> struct Node//树结点结构体 { Node *lchild;//左儿子指针 Node *rchild;//右儿子指针 int c;//保存数字 }Tree[110];//静态内存分配数组 int loc;//静态数组中被使用元素的个数,方便定位结点位置 Node *creat() //申请一个结点空间,返回指向其的指针 { Tree[loc].lchild = Tree[loc].rchild = NULL;//初始化左右儿子为空 return &Tree[loc++];//返回指针,且loc累加 } void postOrder(Node *T)//后序遍历 { if (T->lchild != NULL)postOrder(T->lchild);//左子树不为空,递归遍历左子树 if (T->rchild != NULL)postOrder(T->rchild);//右子树不为空,递归遍历右子树 printf("%d ", T->c);//遍历该结点,输出其字符信息 } void inOrder(Node *T)//中序遍历 { if (T->lchild != NULL)inOrder(T->lchild);//右子树不为空,递归遍历右子树 printf("%d ", T->c);//遍历该结点,输出其字符信息 if (T->rchild != NULL)inOrder(T->rchild);//左子树不为空,递归遍历左子树 } void preOrder(Node *T)//前序遍历 { printf("%d ", T->c);//遍历该结点,输出其字符信息 if (T->lchild != NULL)preOrder(T->lchild);//左子树不为空,递归遍历左子树 if (T->rchild != NULL)preOrder(T->rchild);//右子树不为空,递归遍历右子树 } Node* Insert(Node *T, int x)//插入数字 { if (T == NULL)//若当前树为空 { T = creat();//建立结点 T->c = x;//数字直接插入其根结点 return T;//返回根结点指针 } else if (x < T->c) T->lchild = Insert(T->lchild, x);//若x数值小于根结点,插入到左子树 else if (x > T->c) T->rchild = Insert(T->rchild, x);//若x数值大于根结点,插入到右子树 return T;//返回根结点指针,x数值和根结点相同时,应题目要求直接忽略 } int main() { int n; while (scanf("%d", &n) != EOF) { loc = 0; Node *T = NULL;//二叉排序树树根节点为空 for (int i = 0; i < n; i++)//依次读入n个数字 { int x; scanf("%d", &x); T = Insert(T, x);//插入到排序树中 } preOrder(T);//前序遍历 printf(" "); inOrder(T);//中序遍历 printf(" "); postOrder(T);//后序遍历 printf(" "); } return 0; }

#include<cstdio> #include<cstring> #include<iostream> using namespace std; int n, loc;//元素总数,下标 struct Node { Node* l; Node* r; int x; }t[105]; Node* create() { t[loc].l = t[loc].r = NULL; return &t[loc++]; } Node* Insert(int num, Node* root) { if (root == NULL) { root = create(); root->x = num; return root; } else if (root->x > num)root->l = Insert(num, root->l); else if (root->x < num)root->r = Insert(num, root->r); return root; } void preOrder(Node* root) { printf("%d ", root->x); if (root->l != NULL)preOrder(root->l); if (root->r != NULL)preOrder(root->r); } void inOrder(Node* root) { if (root->l != NULL)inOrder(root->l); printf("%d ", root->x); if (root->r != NULL)inOrder(root->r); } void postOrder(Node* root) { if (root->l != NULL)postOrder(root->l); if (root->r != NULL)postOrder(root->r); printf("%d ", root->x); } int main() { while (scanf("%d", &n) != EOF) { loc = 0; Node* tree = NULL; for (int i = 0; i < n; i++) { int tmp; scanf("%d", &tmp); tree = Insert(tmp, tree); } preOrder(tree); printf(" "); inOrder(tree); printf(" "); postOrder(tree); printf(" "); } return 0; }
在学习了二叉排序树的建立和三种方式的遍历以后,我们还要接触一种特殊的树操作——判断两棵二叉树是否相同。
判断两棵树是否相同,我们不能简单的用某一种遍历方式去遍历两棵树,并判断遍历的结果是否相同,这种方法是错误的。由于一种遍历顺序并不能唯一地确定一棵二叉树,所以两棵不同的树的某一种遍历顺序是可能相同的。如数字相同,插入顺序不同而建立的两棵二叉排序树,它们的中序遍历一定是一样的。但在之前例题中我们已经看到,包括中序遍历在内的两种遍历结果可以唯一得确定一棵二叉树,那么我们只需对两棵树进行包括中序遍历在内的两种遍历,若两种遍历的结果都相同,那么就可以判定两棵树是完全相同的。
例 3.6 二叉搜索树(题目要求就是判断两颗二叉排序树是否相同,二叉搜索树就是排序树)
AC代码
#include<cstdio> #include<cstring> struct Node//树结点结构体 { Node *lchild;//左儿子指针 Node *rchild;//右儿子指针 int c;//保存数字 }Tree[110];//静态内存分配数组 int loc;//静态数组中被使用元素的个数,方便定位结点位置 Node *creat() //申请一个结点空间,返回指向其的指针 { Tree[loc].lchild = Tree[loc].rchild = NULL;//初始化左右儿子为空 return &Tree[loc++];//返回指针,且loc累加 } char str1[25], str2[25];//保存二叉排序树的遍历结果,将每一棵树的前序遍历得到的字符串和中序遍历得到的字符串连接,得到遍历结果字符串 int size1, size2;//保存在字符数组中的遍历得到的字符个数 char * str;//当前正在保存的字符串 int *size;//当前正在保存的字符串的字符个数 void postOrder(Node *T)//后序遍历 { if (T->lchild != NULL)postOrder(T->lchild);//左子树不为空,递归遍历左子树 if (T->rchild != NULL)postOrder(T->rchild);//右子树不为空,递归遍历右子树 str[(*size)++] = T->c + '0';//将该结点中的字符放入正在保存的字符串中 } void inOrder(Node *T)//中序遍历 { if (T->lchild != NULL)inOrder(T->lchild);//右子树不为空,递归遍历右子树 str[(*size)++] = T->c + '0'; if (T->rchild != NULL)inOrder(T->rchild);//左子树不为空,递归遍历左子树 } Node* Insert(Node *T, int x)//插入数字 { if (T == NULL)//若当前树为空 { T = creat();//建立结点 T->c = x;//数字直接插入其根结点 return T;//返回根结点指针 } else if (x < T->c) T->lchild = Insert(T->lchild, x);//若x数值小于根结点,插入到左子树 else if (x > T->c) T->rchild = Insert(T->rchild, x);//若x数值大于根结点,插入到右子树 return T;//返回根结点指针,x数值和根结点相同时,应题目要求直接忽略 } int main() { int n; char tmp[12]; while (scanf("%d", &n) != EOF && n != 0) { loc = 0; Node *T = NULL;//二叉排序树树根节点为空 scanf("%s", tmp);//输入字符串 for (int i = 0; tmp[i] != 0; i++)T = Insert(T, tmp[i] - '0');//按顺序将数字插入二叉搜索树 size1 = 0;//保存在第一个字符串中的字符初始化为0 str = str1;//将正在保存的字符串设定为第一个字符串 size = &size1;//将正在保存字符串中的字符个数指针指向size1 postOrder(T); inOrder(T); str1[size1] = 0;//向第一个字符串的最后一个字符后添加空字符,方便使用字符串函数 while (n-- != 0)//输入其他n个字符串 { scanf("%s", tmp); Node *T2 = NULL; for (int i = 0; tmp[i] != 0; i++)T2 = Insert(T2, tmp[i] - '0');//建立二叉排序树 size2 = 0;//保存在第二个字符串中的字符初始化为0 str = str2;//将正在保存的字符串设定为第二个字符串 size = &size2;//将正在保存字符串中的字符个数指针指向size2 postOrder(T2); inOrder(T2); str2[size2] = 0; puts(strcmp(str1, str2) == 0 ? "YES" : "NO");//比较两个遍历字符串 } } return 0; }
同样的,我们也可以选择中序和后序的排序结果共同对两棵树进行判定。但是请注意,在选择的两种遍历方式中必须要包括中序遍历。如在数据结构中所讲的,只有包括中序的两种遍历顺序才能唯一的确定一棵二叉树。
最后,我们对二叉排序树的删除作适当的补充。二叉排序树的删除在机试题中考察的概率非常小,在之前我们已经得到的机试题中没有对其进行任何的考察。
要删除二叉排序树上的某一个结点,我们按如下步骤进行:
1.利用某种遍历找到该结点。
2.若该结点为叶子结点,则直接删除它,即将其双亲结点中指向其的指针改为 NULL。释放该节点空间。
3.若该结点仅不存在右子树,则直接将其左子树的根结点代替其位置后,删除该结点。即将其双亲结点指向其的指针改为指向其的左子树树根。
4.若该节点存在右子树,则找到右子树上最右下的结点(即中序遍历中该子树上第一个被遍历到的结点),将被删除结点的数值改为右子树上最右下结点的数值后,删除最右下结点。
删除二叉树的原理非常简单,即删除该结点后,其中序遍历依然保持关键字递增的顺序,只要符合这个条件,不同于上述规则的删除也是可行的。
