LeetCode探索初级算法 - 动态规划
今天在LeetCode上做了几个简单的动态规划的题目,也算是对动态规划有个基本的了解了。现在对动态规划这个算法做一个简单的总结。
什么是动态规划
动态规划英文 Dynamic Programming,是求解决策过程最优化的数学方法,后来沿用到了编程领域。
动态规划的大致思路是把一个复杂的问题转化成一个分阶段逐步递推的过程,从简单的初始状态一步一步递推,最终得到复杂问题的最优解。
动态规划解决问题的过程分为两步:
- 寻找状态转移方程
- 利用状态转移方程式自底向上求解问题
在这里先向大家推荐一篇文章,也是讲动态规划的,用漫画的形式讲解,生动活泼,浅显易懂。
例题
话不多说,直接看看题目。
1.爬楼梯
题目描述
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
注意:给定 n 是一个正整数。
示例 1:
输入: 2
输出: 2
解释: 有两种方法可以爬到楼顶。
1. 1 阶 + 1 阶
2. 2 阶
示例 2:
输入: 3
输出: 3
解释: 有三种方法可以爬到楼顶。
1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶
爬楼梯问题是动态规划算法中非常经典的一道题目,出场率十分高。现在我尝试循序渐进地把这个问题讲清楚。
思路
我们设置一个函数F(N)来表示走到第N级台阶走法的数量,现在假设有10级台阶。现在就会出现两种情况:
- 我们是从第9级,跨1级上来,到第10级
- 我们是从第8级,跨2级上来,到第10级
其实对于任何第N级台阶,都会出现这两种情况,即第N级的前一步是走了1级或者两级。
所以如果我们统计F(10)的话,可以发现F(10) = F(9) + F(8),即到第10级的走法等于到第9级的走法加上到第8级的走法。同理可得,F(9) = F(8) + F(7),F(8) = F(7) + F(6)等等等等……
所以我们就得到了动态规划步骤1中的所说的所谓的状态转移方程:F(N) = F(N-1) + F(N-2).
一直到最底层,当只有1级台阶时,F(1) = 1;当只有2级台阶时F(2) = 2.
到这里,直觉告诉我们可以用递归来解决这个问题。
递归法
public int climbStairs (int n) {
if (n < 1) {
return 0;
}
if (n == 1) {
return 1;
}
if (n == 2) {
return 2;
}
return climbStairs(n - 1) + climbStairs(n - 2);
}
但是递归法有个问题,时间复杂度比较高。我们可以看一下下图:
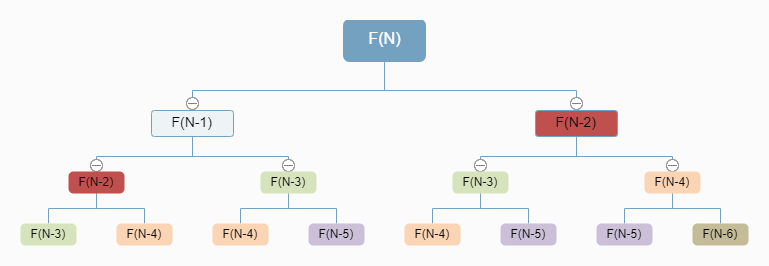
递归的过程可以构造出一棵二叉树,可以看出求解F(N)过程中,会访问(2^N)次F()函数,即时间复杂度为(O(2^N)).并且,递归的过程中包含着大量的重复操作,二叉树越往下走,重复操作越多,上图中相同颜色标出的节点就是表示重复的操作。
那怎么解决这个问题呢?现在我们就要搬出动态规划的步骤2了,采用自底向上的方法求解问题。
刚才的递归法,我们是从第10级台阶往下,计算F(9)和F(8),再计算F(9)需要的F(8)和F(7),以及F(8)需要的F(7)和F(6),依次往下,体现在二叉树上,就是从最顶上的节点往下构造出这棵二叉树。
现在我们转化思路,自底向下构造。我们现在已经知道了F(1)=1和F(2)=2,所以我们可以知道F(3) = F(2) + F(1) = 3,进一步地,我们可以知道F(4) = F(3) + F(2) = 5,等等等等……
按照这个方法,我们可以设置一个数组,依次往里面填数就可以了。时间复杂度为(O(N))。
动态规划法
public int climbStairs (int n) {
if (n == 1){
return 1;
}// 防止数组越界
int[] step = new int[n + 1];
step[1] = 1;
step[2] = 2;
for (int i = 3; i <= n; i++) {
step[i] = step[i - 1] + step[i - 2];
}
return step[n];
}
2. 最大子序和
题目描述
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
示例:
输入: [-2,1,-3,4,-1,2,1,-5,4],
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。
思路
废话不多说,我们直接走动态规划的流程。第一步就是寻找状态转移方程。
其实这个状态转移方程有点像高中数学里面的数列的通项公式,数列的通项公式可以通过各种各样的方法找出来,什么规律法、累加累乘什么的,我们这里找动态规划的状态转移方程就比较类似于规律法找通项公式,这个通项公式就是第N项与前若干项之间的关系。
我们看这个题目,我们遍历一遍数组,假如我们现在正站在第i个元素,如何通过第i个元素的值和前面若干个元素的值来找到所谓的最大子序和呢?
最大子序和,我们当然是想让一个子序中正数越多越好,负数越少越好。所以假如我们现在有一个子序,它是和最大子序的候选人,我们就希望这个子序的后面的元素是正数,从而可以继续增加这个子序的和。换位思考一下,现在我们是一个元素,前面有一个子序,我们就希望前面这个子序的和是正的,我加入这个子序不就抱了大腿吗,要是前面这个子序的和是负的,那完了,我加入前面的子序还要自损一部分功力,还不如单干呢,我自己就当一个子序。
前面的解释,自我感觉还是比较形象的,现在让这个解释与动态规划的编程实现结合起来。
我们定义一个数组dp[],dp[i]是以第i个元素为结尾的一段最大子序和。求dp[i]时,假设前面dp[0]~dp[i-1]都已经求出来了,dp[i-1]表示的是以i-1为结尾的最大子序和,若dp[i-1]小于0,则dp[i]加上前面的任意长度的序列和都会小于不加前面的序列(即自己本身一个元素是以自己为结尾的最大自序和)。
所以状态转移方程相当于是一个判断函数。
if (dp[i - 1] > 0) {
dp[i] = dp[i - 1] + nums[i];
} else {
dp[i] = nums[i];
}
第二步是利用状态转移方程自底向上求解,这和上一道题目类似,按照顺序往数组里面填值。
源码
public int maxSubArray (int[] nums) {
if (nums.length == 0) return 0;
if (nums.length == 1) return nums[0];
int[] dp = new int[nums.length];
dp[0] = nums[0];
int max = dp[0];
for (int i = 1; i < dp.length; i++) {
if (dp[i - 1] > 0) {
dp[i] = dp[i - 1] + nums[i];
} else {
dp[i] = nums[i];
}
max = Math.max(dp[i],max);
}
return max;
}
3. 打家劫舍
题目描述
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你在不触动警报装置的情况下,能够偷窃到的最高金额。
示例 1:
输入: [1,2,3,1]
输出: 4
解释: 偷窃 1 号房屋 (金额 = 1) ,然后偷窃 3 号房屋 (金额 = 3)。
偷窃到的最高金额 = 1 + 3 = 4 。
示例 2:
输入: [2,7,9,3,1]
输出: 12
解释: 偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9),接着偷窃 5 号房屋 (金额 = 1)。
偷窃到的最高金额 = 2 + 9 + 1 = 12 。
思路
废话不多说,我们直接走动态规划的流程。第一步就是寻找状态转移方程。
再重复一遍,状态转移矩阵是第N项与前若干项之间的关系。
现在我们是一个小偷,站在第i家的屋顶,我们是偷,还是不偷呢?这是个问题。
- 如果偷,那前面一家(i-1)我就不能偷,我当前偷到的最大值就是偷完前(i-2)家的最大值加上我偷这一家的钱。
- 如果不偷,我当前偷到的最大值就是偷完前(i-1)加的最大值,然后我就去下一家再看看。
所以状态转移矩阵就可以用如下一个公式表示:
rob(i) = Math.max( rob(i - 2) + currentHouseValue, rob(i - 1) )
第二步是利用状态转移矩阵自底向上求解问题。
我们定义一个数组dp[],dp[i]是以第i个元素为结尾的偷窃到的最大金额。求dp[i]时,假设前面dp[0]~dp[i-1]都已经求出来了。
源码
public int rob(int[] nums) {
if (nums.length == 0) return 0;
int[] dp = new int[nums.length + 1];
dp[0] = 0;
dp[1] = nums[0];
for (int i = 2; i <= nums.length; i++) {
dp[i] = Math.max(dp[i-1],dp[i-2] + nums[i-1]);
}
return dp[nums.length];
}
总结
在利用动态规划求解问题的过程中,比较难的是找到状态转移方程,之前多次提到,状态转移方程是第N项与前若干项之间的关系。这是我个人的一点理解,求动态规划的第i项时可以假设前面的若干项都是已知的了。比如第一题爬楼梯,就是当前项和前两项的关系,最大子序和是当前项取决于前一项的正负,打家劫舍也是看当前项和前两项的关系。
找到这种关系后,需要转化思路,自底向上编写程序,这样才能降低时间复杂度,才是真正的动态规划。