这些问题大多数出自于做过的模拟题,大多数在OJ上都找不到。
因为大部分模拟题不再被允许发博客,所以这个合集停更了。
从这里开始
kand
Problem Descript
给定$n$个数,从中选出$k$个数,问使得它们and和为$s$的方案数。
Input
第一行三个正整数$n$, $k$和$s$。
接下来有$n$行,每行一个整数$a_{i}$表示第$i$个数。
Output
仅一行,一个整数,表示答案对$10^{9} + 7$取模后的结果。
Sample
input
3 2 2
3
2
1output
1
Limit
对于10%的数据满足$1leqslant n leqslant 10, 0 leqslant a_{i}, s leqslant 2^{10}$
对于30%的数据满足$1leqslant n leqslant 100, 0 leqslant a_{i}, s leqslant 2^{10}$
对于70%的数据满足$1leqslant n leqslant 10^{5}, 0 leqslant a_{i}, s leqslant 2^{15}$
对于所有的数据满足$1leqslant n leqslant 10^{5}, 0 leqslant a_{i}, s leqslant 2^{20}$Source
idy002
Solution 1
暴力枚举$k$组合。期望得分10分。
Solution 2
用$f[i][j][k]$表示考虑到前$i$个数中,选出$j$个数,它们的and和为$k$的方案数。
时间复杂度$O(n^{2}2^{W})$,期望得分30分。
Solution 3
当首先过滤掉$s and a_{i} eq s$的数。
当$s$的某一位为0时,那么选出的数至少有一个这一位为0,那么可以考虑容斥。
用所有方案减去存在不合法的方案。
不合法的方案可以枚举每次选出来的数哪几位为1,然后暴力计算$cnt$,用组合数算方案。
时间复杂度$O(3^{W} + n)$,期望得分70分。
Solution 4
发现暴力求$cnt$的过程是FWT的正变换。
于是FWT优化一下就好了。
时间复杂度$O(Wcdot 2^{W} + n)$,期望得分100分。
Code

1 #include <iostream> 2 #include <cstdio> 3 using namespace std; 4 typedef bool boolean; 5 6 const int Val = (1 << 20), mask = Val - 1, M = 1e9 + 7; 7 8 void exgcd(int a, int b, int& d, int& x, int& y) { 9 if (!b) 10 d = a, x = 1, y = 0; 11 else { 12 exgcd(b, a % b, d, y, x); 13 y -= (a / b) * x; 14 } 15 } 16 17 int inv(int a, int n) { 18 int d, x, y; 19 exgcd(a, n, d, x, y); 20 return (x < 0) ? (x + n) : (x); 21 } 22 23 int n, k, s; 24 int *jc, *ijc; 25 int cnt[Val]; 26 27 inline void init() { 28 scanf("%d%d%d", &n, &k, &s); 29 jc = new int[(n + 1)]; 30 ijc = new int[(n + 1)]; 31 int nc = 0, S = s ^ mask; 32 for (int i = 1, x; i <= n; i++) { 33 scanf("%d", &x); 34 if ((s & x) == s) 35 cnt[x & S]++, nc++; 36 } 37 n = nc; 38 } 39 40 inline void prepare() { 41 jc[0] = 1; 42 for (int i = 1; i <= n; i++) 43 jc[i] = jc[i - 1] * 1ll * i % M; 44 ijc[n] = inv(jc[n], M); 45 for (int i = n - 1; ~i; i--) 46 ijc[i] = ijc[i + 1] * 1ll * (i + 1) % M; 47 } 48 49 inline int C(int n, int k) { 50 if (n < k) return 0; 51 return (jc[n] * 1ll * ijc[k]) % M * ijc[n - k] % M; 52 } 53 54 inline void solve() { 55 int ans = C(n, k), S; 56 for (int i = 0; i < 20; i++) { 57 S = mask ^ (1 << i); 58 for (int j = S; j; j = (j - 1) & S) 59 cnt[j] += cnt[j | (1 << i)]; 60 } 61 S = s ^ mask; 62 for (int i = S, sign, j; i; i = (i - 1) & S) { 63 if (cnt[i]) { 64 for (j = i, sign = 1; j; j -= j & (-j), sign *= -1); 65 ans = (ans + sign * C(cnt[i], k)) % M; 66 if (ans < 0) ans += M; 67 } 68 } 69 printf("%d ", ans); 70 } 71 72 int main() { 73 freopen("kand.in", "r", stdin); 74 freopen("kand.out", "w", stdout); 75 init(); 76 prepare(); 77 solve(); 78 return 0; 79 }
青蛙


Solution 1
直接暴力枚举所有情况。
时间复杂度$O(2^{m})$。期望得分20分。
Solution 2
设当前考虑第$i$只青蛙跳跃。
那么这次后,它结束的位置的期望是$x_{i}' = frac{x_{i} - 2(x_{i} - x_{i - 1}) + x_{i} - 2(x_{i} - x_{i + 1})}{2}=x_{i + 1} + x_{i - 1} - x_{i}$。
然后暴力递推。时间复杂度$O(mk)$。期望得分40分。
Solution 3
暴力打表可以发现在$n, m geqslant 10^{3}$时,随即数据下,操作的循环节大约在$5000$左右。
然后找一下循环节,就可以骗到70分。
Solution 4
可以发现一个有趣的事情:
$x_{i}' - x_{i - 1}= x_{i + 1} - x_{i}$
$x_{i + 1} - x_{i}' = x_{i} - x_{i - 1}$
这相当于一次操作交换了相邻的两个差。
这个可以看成一个置换。可以处理出一轮操作的置换,最终的差分数组等于先把这个置换进行$k$次幂,然后作用在原来的差分数组上。
由于置换的合成是$O(n)$的,所以可以直接快速幂,时间复杂度$O(nlog k)$
也可以把置换看成轮换,把中间每个环拉出来,然后往前走$k$步,时间复杂度$O(n)$。
期望得分100分。
由于我比较懒,就只给出快速幂的代码。
Code

1 #include <iostream> 2 #include <cstring> 3 #include <cstdio> 4 #ifndef WIN32 5 #define Auto "%lld" 6 #else 7 #define Auto "%I64d" 8 #endif 9 using namespace std; 10 11 #define ll long long 12 13 const int N = 1e5 + 5; 14 15 typedef class MyVector { 16 public: 17 int a[N]; 18 19 MyVector() { } 20 MyVector(int n) { 21 for (int i = 1; i <= n; i++) 22 a[i] = i; 23 } 24 MyVector(int* ar, int n) { 25 for (int i = 1; i <= n; i++) 26 a[ar[i]] = i; 27 } 28 29 int& operator [] (int p) { 30 return a[p]; 31 } 32 }MyVector; 33 34 int n, m; 35 ll k; 36 int *ar, *qr; 37 int *da, *nda; 38 39 MyVector operator * (MyVector a, MyVector b) { 40 MyVector rt; 41 for (int i = 1; i < n; i++) 42 rt[i] = a[b[i]]; 43 return rt; 44 } 45 46 MyVector qpow(MyVector& a, ll pos) { 47 MyVector pa = a, rt(n - 1); 48 for ( ; pos; pos >>= 1, pa = pa * pa) 49 if (pos & 1) 50 rt = pa * rt; 51 return rt; 52 } 53 54 inline void init() { 55 scanf("%d", &n); 56 ar = new int[(n + 1)]; 57 qr = new int[(n + 1)]; 58 da = new int[(n + 1)]; 59 nda = new int[(n + 1)]; 60 for (int i = 1; i < n; i++) 61 qr[i] = i; 62 for (int i = 1; i <= n; i++) 63 scanf("%d", ar + i); 64 for (int i = 1; i < n; i++) 65 da[i] = ar[i + 1] - ar[i]; 66 scanf("%d"Auto, &m, &k); 67 for (int i = 1, x; i <= m; i++) { 68 scanf("%d", &x); 69 swap(qr[x - 1], qr[x]); 70 } 71 } 72 73 MyVector a; 74 75 inline void solve() { 76 a = MyVector(qr, n - 1); 77 a = qpow(a, k); 78 for (int i = 1; i < n; i++) 79 nda[a[i]] = da[i]; 80 ll ps = ar[1]; 81 printf(Auto" ", ps); 82 for (int i = 1; i < n; i++) { 83 ps += nda[i]; 84 printf(Auto" ", ps); 85 } 86 } 87 88 int main() { 89 freopen("frog.in", "r", stdin); 90 freopen("frog.out", "w", stdout); 91 init(); 92 solve(); 93 return 0; 94 }
dalao


注:因为样例2有错所以被我删掉了。
Solution 1
暴力枚举每一对$(x, y)$
时间复杂度$O(n^{2})$,期望得分10分。
Solution 2
经典的三维偏序问题。
可以CDQ分治或者树套树。
时间复杂度$O(n log ^{2} n)$,期望得分60 ~ 100分。(某ZJC加上各种毒瘤优化,卡进时限4s,实际上时间限制可以只开2s)。
Solution 3
设$K_{x, y} = [a_{x} < a_{y}] + [b_{x} < b_{y}] + [c_{x} < c_{y}]$
$S_{x, y} = max {K_{x, y}, K_{y, x}}$。
显然$S_{x, y} in {2, 3}$。
设$A = sum_{1leqslant x < y leqslant n}[S_{x, y} = 3]$, $B = sum_{1leqslant x < y leqslant n}[S_{x, y} = 2]$。
那么$A$就是问题所要我们求的。
另外,设$P_{a, b} = sum_{1 leqslant x, y leqslant n}[a_{x} < a_{y}][b_{x} < b_{y}]$。
有注意到$A + B = C_{n}^{2}$。然后细心会发现:
$3 imes A + B =P_{a, b} + P_{a, c} + P_{b, c}$
因为每一对合法的无序对$(x, y)$都会对右边的式子作出3次贡献,不合法的无序对会对右边的式子作出1次贡献。
然后根据这两个式子解解方程就能得到$A$了。
时间复杂度$O(n log n)$,期望得分100分。
Code

1 #include <iostream> 2 #include <cstdlib> 3 #include <cstring> 4 #include <cstdio> 5 #include <ctime> 6 #ifndef WIN32 7 #define Auto "%lld" 8 #else 9 #define Auto "%I64d" 10 #endif 11 using namespace std; 12 typedef bool boolean; 13 14 #define ll long long 15 16 typedef class IndexedTree { 17 public: 18 int s; 19 int* ar; 20 21 IndexedTree() { } 22 IndexedTree(int n):s(n) { 23 ar = new int[(n + 1)]; 24 memset(ar, 0, sizeof(int) * (n + 1)); 25 } 26 27 void add(int idx, int x) { 28 for ( ; idx <= s; idx += (idx & (-idx))) 29 ar[idx] += x; 30 } 31 32 int getSum(int idx) { 33 int rt = 0; 34 for ( ; idx; idx -= (idx & (-idx))) 35 rt += ar[idx]; 36 return rt; 37 } 38 }IndexedTree; 39 40 int myrand(int& seed) { 41 return seed = ((seed * 19260817ll) ^ 233333) & ((1 << 24) - 1); 42 } 43 44 void gen(int* ar, int s, int n) { 45 for (int i = 1; i <= n; i++) ar[i] = i; 46 for (int i = 1; i <= n; i++) swap(ar[i], ar[myrand(s) % i + 1]); 47 } 48 49 int n; 50 ll res = 0; 51 int *ar, *br, *cr; 52 int *ls; 53 IndexedTree it; 54 55 inline void init() { 56 scanf("%d", &n); 57 int sa, sb, sc; 58 scanf("%d%d%d", &sa, &sb, &sc); 59 ar = new int[(n + 1)]; 60 br = new int[(n + 1)]; 61 cr = new int[(n + 1)]; 62 ls = new int[(n + 1)]; 63 it = IndexedTree(n); 64 gen(ar, sa, n); 65 gen(br, sb, n); 66 gen(cr, sc, n); 67 } 68 69 ll calc(int* ar, int* br) { 70 for (int i = 1; i <= n; i++) 71 ls[ar[i]] = br[i]; 72 ll rt = 0; 73 memset(it.ar, 0, sizeof(int) * (n + 1)); 74 for (int i = 1; i <= n; i++) { 75 rt += it.getSum(ls[i]); 76 it.add(ls[i], 1); 77 } 78 return rt; 79 } 80 81 inline void solve() { 82 res = calc(ar, br); 83 res += calc(ar, cr); 84 res += calc(br, cr); 85 res -= n * 1ll * (n - 1) / 2; 86 res /= 2; 87 printf(Auto, res); 88 } 89 90 int main() { 91 freopen("dalao.in", "r", stdin); 92 freopen("dalao.out", "w", stdout); 93 init(); 94 solve(); 95 return 0; 96 }
区间


Solution 1
找出所有连续区间。然后用dp的思想去更新答案就好了。
时间复杂度$O(n^{2} + m)$,期望得分30分、
Solution 2
由于是一个排列,所以式子可以写成$max - min = r - l$。考虑暴力找连续区间的过程是枚举$l$,然后再枚举$r$的过程。当$l$不变的时候,$r$递增,如果$max$和$min$均为改变有一点小浪费。
因此可以考虑将$max$和$min$分段,然后每段每段地跳,每跳一次段可以直接计算出位置,然后判断一下是否合法。
时间复杂度$O(n^{2} + m)$,期望得分30 ~ 70分、
Solution 3
注意到两个连续区间如果存在公共部分,那么将它们合并后也一定是一个连续区间。
因为这是一个排列,所以将公共部分去掉后的两个区间的值域不会相交。不难证明两个连续区间合并的值域长度等于新区间的长度。
因此可以考虑CDQ分治。假设当前分治区间$[l, r]$,分治中心$mid$。
我可以枚举一个$l'$然后找到一个最短的包含区间$[l', mid + 1]$的区间。
这个可以用一个st表存值的大小,一个st表存一个值对应的下标。
当要求包含区间$[l, r]$的时候,可以在第一个st表中查询这一段的最大值和最小值,然后在第二个st表中查询这一段值域中的每个值在原数组中出现的下标的最大值r'和最小值l'。也就是意味着要包含区间$[l', r']$,于是便可以这样迭代去查。终止条件是$l' = l, r' = r$。
不理解st表维护的信息?那么换个解释方法,前者对数组$a_{i}$的区间最大最小值建立st表,后者对数组$b_{a_{i}} = i$的区间最大最小值建立st表。
但是这样做时间复杂度有问题,不可能每个位置都去查找一次。
可以继续发现一些优美性质:
性质1 如果存在四个整数满足$1 leqslant l' < l leqslant r' < r leqslant n$,且使得$[l', r'],[l, r]$是连续的,那么$[l', r]$也是连续的。
证明 因为这是一个排列,所以非公共部分的值域是没有交集的。因此公共部分的值域是连续的。所以$[l', r]$也是连续的。
性质2 分治时,当要找到包含区间$[l', mid + 1]$时,且长度尽量小,可选的区间是唯一的。
证明 假设存在两个候选区间$[a, b],[c,d]$且满足$b - a = d - c, lleqslant a < c leqslant l' < mid + 1 leqslant b < d leqslant r$。
那么根据性质1,可以找到区间$[c, b]$作为答案。显然$b - c < d - c$,与候选区间要求满足的性质矛盾。
也许有些人会有点怀疑这个迭代做法的正确性,这个过程中,暂时先不考虑时间复杂度的问题。
算法的正确性 如果枚举左端点$l'$,那么找到的合法区间$[a, b]$是长度最小的。
证明 合法性 根据迭代终止条件和迭代过程易证(一个是要求连续,一个是要求包含$[l', mid + 1]$)。
最优性 假设存在一个更优的区间$[c, d]$,根据性质2,我们有$a < c, d leqslant b$或$a leqslant c, d < b$,因为要求包含$[l', mid + 1]$,而迭代是先从这个区间开始的,所以必然存在一个区间$[e, f]$恰好被$[c, d]$包含并且迭代的下一个区间没有被$[c, d]$包含(PS:如果下一个区间恰好为$[c, d]$,易证它不合法)。因此$[e, f]$的最小值和最大值之间每一个数都要在$[c, d]$中出现,但是根据迭代过程可知,必然存在一个$x$,使得它存在于$[e, f]$的最小值和最大值之间,但不在$[c, d]$中,因此$[c, d]$不是一个连续区间,与题目要求矛盾。
所以综上所述,算法是正确的。
现在来考虑优化。
性质3 当枚举的左端点单调递减时,右端点不减。
证明 仍然考虑反证法。假设枚举存在两个最优区间$[a, b], [c, d]$,满足$l leqslant a < c leqslant b < d leqslant r$。
根据性质1,$[c, b]$是一个更优的答案。因此$[c, d]$不是最优的区间,矛盾。
有了这种优美的性质,不难得到,每次找到的区间是真包含前一个区间。
所以对于上一个找到的区间$[a, b]$。我只要再将$a + 1$然后继续用迭代法去找下一个区间就行了。
对于右边我们仍然做一次类似的过程:枚举$r'$,找到包含区间$[mid, r']$的一些区间。
然后这有什么用呢?
这个过程找到了一系列左端点递减的跨过分治中心的合法区间和一系列右端点递增的跨过分治中心的合法区间。
对于查询一个区间$[l', r'], l leqslant l' leqslant r' leqslant r$,我在左边找到一个左端点小于等于$l'$的区间,在右边找到一个右端点大于等于$r'$的区间。然后将这两个区间取并集(注意是取并集!)尝试去更新这个询问的答案。
这个方法很多,可以二分。由于值域很小,也可以直接求前后缀最值。
时间复杂度$O(nlog n + mlog n)$,期望得分100分。
Code

1 #include <algorithm> 2 #include <iostream> 3 #include <cassert> 4 #include <cstring> 5 #include <cstdio> 6 #include <vector> 7 using namespace std; 8 typedef bool boolean; 9 10 const int N = 1e5 + 5, bzmax = 18; 11 12 #define pii pair<int, int> 13 #define fi first 14 #define sc second 15 16 pii operator + (pii a, pii b) { 17 return pii(min(a.fi, b.fi), max(a.sc, b.sc)); 18 } 19 20 boolean operator < (pii a, pii b) { 21 return a.sc - a.fi < b.sc - b.fi; 22 } 23 24 typedef class SparseTable { 25 public: 26 int log2[N]; 27 pii f[N][18]; 28 29 SparseTable() { } 30 SparseTable(int n, int *ar) { 31 log2[1] = 0; 32 for (int i = 2; i <= n; i++) 33 log2[i] = log2[i >> 1] + 1; 34 for (int i = 1; i < n; i++) 35 f[i][0] = pii(ar[i], ar[i]) + pii(ar[i + 1], ar[i + 1]); 36 for (int j = 1; j < bzmax; j++) 37 for (int i = 1; i + (1 << j) <= n; i++) 38 f[i][j] = f[i][j - 1] + f[i + (1 << (j - 1))][j - 1]; 39 } 40 41 pii query(int a, int b) { 42 assert(a != b); 43 int p = log2[b - a]; 44 return f[a][p] + f[b - (1 << p)][p]; 45 } 46 }SparseTable; 47 48 typedef class Query { 49 public: 50 int l, r; 51 pii res; 52 }Query; 53 54 int n, m; 55 int *ar, *var; 56 Query *qs; 57 pii *ls, *rs; 58 SparseTable st1, st2; 59 60 inline void init() { 61 scanf("%d", &n); 62 ar = new int[(n + 1)]; 63 var = new int[(n + 1)]; 64 for (int i = 1; i <= n; i++) 65 scanf("%d", ar + i); 66 for (int i = 1; i <= n; i++) 67 var[ar[i]] = i; 68 scanf("%d", &m); 69 qs = new Query[(n + 1)]; 70 for (int i = 1; i <= m; i++) 71 scanf("%d%d", &qs[i].l, &qs[i].r), qs[i].res = pii(1, n); 72 } 73 74 void dividing(int l, int r, vector<Query*>& qs) { 75 if (qs.empty()) return; 76 if (l == r) { 77 for (int i = 0; i < (signed) qs.size(); i++) 78 qs[i]->res = pii(l, l); 79 return; 80 } 81 int mid = (l + r) >> 1; 82 vector<Query*> ql, qr; 83 for (int i = 0; i < (signed) qs.size(); i++) 84 if (qs[i]->r <= mid) 85 ql.push_back(qs[i]); 86 else if (qs[i]->l > mid) 87 qr.push_back(qs[i]); 88 89 dividing(l, mid, ql); 90 dividing(mid + 1, r, qr); 91 92 int tl = 0, tr = 0; 93 pii cur, nx, p1, p2; 94 for (nx = cur = pii(mid, mid + 1); cur.fi >= l && cur.sc <= r; cur.fi--) { 95 do { 96 nx = st1.query(cur.fi, cur.sc); 97 nx = st2.query(nx.fi, nx.sc); 98 } while (cur != nx && (cur = nx).fi >= l && cur.sc <= r); 99 if (cur.fi >= l && cur.sc <= r) 100 ls[++tl] = cur; 101 } 102 103 for (nx = cur = pii(mid, mid + 1); cur.fi >= l && cur.sc <= r; cur.sc++) { 104 do { 105 nx = st1.query(cur.fi, cur.sc); 106 nx = st2.query(nx.fi, nx.sc); 107 } while (cur != nx && (cur = nx).fi >= l && cur.sc <= r); 108 if (cur.fi >= l && cur.sc <= r) 109 rs[++tr] = cur; 110 } 111 112 int l1, l2, r1, r2; 113 Query *q; 114 for (int i = 0; i < (signed) qs.size(); i++) { 115 q = qs[i]; 116 if (q->l < ls[tl].fi || q->r > rs[tr].sc) continue; 117 l1 = 1, r1 = tl, l2 = 1, r2 = tr; 118 while (l1 <= r1) { 119 mid = (l1 + r1) >> 1; 120 if (ls[mid].fi <= q->l) 121 r1 = mid - 1; 122 else 123 l1 = mid + 1; 124 } 125 126 while (l2 <= r2) { 127 mid = (l2 + r2) >> 1; 128 if (rs[mid].sc >= q->r) 129 r2 = mid - 1; 130 else 131 l2 = mid + 1; 132 } 133 cur = (ls[r1 + 1] + rs[r2 + 1]); 134 if (cur < q->res) 135 q->res = cur; 136 } 137 qs.clear(); 138 } 139 140 vector<Query*> vs; 141 inline void solve() { 142 ls = new pii[(n + 1)]; 143 rs = new pii[(n + 1)]; 144 for (int i = 1; i <= m; i++) 145 vs.push_back(qs + i); 146 st1 = SparseTable(n, ar); 147 st2 = SparseTable(n, var); 148 dividing(1, n, vs); 149 for (int i = 1; i <= m; i++) 150 printf("%d %d ", qs[i].res.fi, qs[i].res.sc); 151 } 152 153 int main() { 154 freopen("interval.in", "r", stdin); 155 freopen("interval.out", "w", stdout); 156 init(); 157 solve(); 158 return 0; 159 }
Lasting Moment·改
*因为版权原因不得公示题面,只给出大意和数据范围。
Main idea
给定一个长串$S$,然后多次询问一个串$S'_{i}$,求$S$长度最短的子串使得$S'_{i}$至少在这个子串中出现了$K_{i}$次,输出它的长度。无解输出-1。
保证每次询问的串互不相同,总串长不超过$10^5$。
Limits
对于所有数据,$1leqslant |S|, Q, sum |S'_{i}|leqslant 10^5$
- 子任务1:$1leqslant |S|, Q, sum |S'_{i}|leqslant 10^3$,空间限制256M
- 子任务2:$1leqslant |S|, Q, sum |S'_{i}|leqslant 10^4$,空间限制256M
- 子任务3:$1leqslant |S|, Q, sum |S'_{i}|leqslant 10^5$,空间限制256M
- 子任务4:$1leqslant |S|, Q, sum |S'_{i}|leqslant 10^5$,强制在线,空间限制16M
Solution 1
使用KMP暴力进行匹配,求出所有匹配位,然后利用相邻的$K$个更新答案。
时间复杂度$O(|S|Q + sum |S|)$。
能够通过子任务1。
Solution 2
性质4 设$n = |S|$,所有匹配点的总个数不超过$2nsqrt{sum|S'_{i}|}$。
证明 考虑对于长度为$k$的所有询问串,最多可能产生的匹配点总个数为$n - k + 1$。
考虑最坏的情况下,询问一个长度为$k$的串,产生了$n - k + 1 leqslant n$个匹配点。
这样至多可以询问$2sqrt{sum|S'_{i}|}$。因此得证。
然后考虑快速用数据结构找到所有匹配点。
比如后缀数组。我们可以在后缀数组中二分找到第一个以及最后一个把$S'_{i}$作为前缀的后缀。设$L = |S'_{i}|$,那么后缀数组中这一段的后缀都包含它作为前缀。
可以把这一段的sa暴力提取出来排序。然后做法同上。
时间复杂度$O(nsqrt{sum|S'_{i}|}log n)$。可以通过子任务1和子任务2。
Solution 3
对询问串建立Trie树。暴力跳last,存下匹配点。最后暴力算答案。
时间复杂度$O(nsqrt{sum|S'_{i}|})$,可以通过子任务1和子任务2,3。
Solution 4
把解法2的排序改成基数排序,桶大小256或者512,可以通过所有数据(不含Extra Test)。
Code

1 #include <algorithm> 2 #include <iostream> 3 #include <cassert> 4 #include <cstdlib> 5 #include <cstring> 6 #include <cstdio> 7 using namespace std; 8 typedef bool boolean; 9 #define ll long long 10 11 const int N = 1e5 + 5, bzmax = 20; 12 13 typedef class Pair3 { 14 public: 15 int x, y, id; 16 17 Pair3(int x = 0, int y = 0, int id = 0):x(x), y(y), id(id) { } 18 }Pair3; 19 20 int n, q; 21 char str[N << 1]; 22 int sa[N], rk[N], cnt[N]; 23 Pair3 xs[N], ys[N]; 24 char buf[N]; 25 26 inline void init() { 27 scanf("%s", str + 1); 28 n = strlen(str + 1); 29 scanf("%d", &q); 30 } 31 32 void radix_sort(Pair3* xs) { 33 int m = max(n, 256); 34 memset(cnt, 0, sizeof(int) * (m + 1)); 35 for (int i = 1; i <= n; i++) 36 cnt[xs[i].y]++; 37 for (int i = 1; i <= m; i++) 38 cnt[i] += cnt[i - 1]; 39 for (int i = 1; i <= n; i++) 40 ys[cnt[xs[i].y]--] = xs[i]; 41 42 memset(cnt, 0, sizeof(int) * (m + 1)); 43 for (int i = 1; i <= n; i++) 44 cnt[ys[i].x]++; 45 for (int i = 1; i <= m; i++) 46 cnt[i] += cnt[i - 1]; 47 for (int i = n; i; i--) 48 xs[cnt[ys[i].x]--] = ys[i]; 49 } 50 51 void build_sa() { 52 for (int i = 1; i <= n; i++) 53 rk[i] = str[i]; 54 for (int k = 0, dif; k < bzmax; k++) { 55 for (int i = 1; i + (1 << k) <= n; i++) 56 xs[i] = Pair3(rk[i], rk[i + (1 << k)], i); 57 for (int i = n - (1 << k) + 1; i <= n; i++) 58 xs[i] = Pair3(rk[i], 0, i); 59 radix_sort(xs); 60 rk[xs[1].id] = dif = 1; 61 for (int i = 2; i <= n; i++) 62 rk[xs[i].id] = ((xs[i].x != xs[i - 1].x || xs[i].y != xs[i - 1].y) ? (++dif) : (dif)); 63 if (dif == n) 64 break; 65 } 66 for (int i = 1; i <= n; i++) 67 sa[rk[i]] = i; 68 } 69 70 int cnt1[512]; 71 int ar[N], br[N]; 72 void radix_sort(int* ar, int len) { 73 const int temp = 511; 74 boolean aflag = true; 75 reverse(ar, ar + len); 76 for (int i = 1; i < len; i++) 77 if (ar[i] < ar[i - 1]) 78 aflag = false; 79 if (aflag) 80 return; 81 int *x = ar, *y = br; 82 for (int t = 0; t < 2; t++) { 83 int bit = t * 9; 84 memset(cnt1, 0, sizeof(cnt1)); 85 for (int i = 0; i < len; i++) 86 cnt1[(x[i] >> bit) & temp]++; 87 for (int i = 1; i <= temp; i++) 88 cnt1[i] += cnt1[i - 1]; 89 for (int i = len - 1; ~i; i--) 90 y[--cnt1[(x[i] >> bit) & temp]] = x[i]; 91 swap(x, y); 92 } 93 for (int i = 0; i < len; i++) 94 ar[i] = x[i]; 95 } 96 97 inline void solve() { 98 int K, len; 99 while (q--) { 100 scanf("%d%s", &K, buf + 1); 101 len = strlen(buf + 1); 102 103 int L = 1, R = n, l, r; 104 for (int i = 1; i <= len && L <= R; i++) { 105 l = L, r = R; 106 while (l <= r) { 107 int mid = (l + r) >> 1; 108 if (str[sa[mid] + i - 1] >= buf[i]) 109 r = mid - 1; 110 else 111 l = mid + 1; 112 } 113 L = r + 1; 114 if (L > R) 115 break; 116 l = L, r = R; 117 while (l <= r) { 118 int mid = (l + r) >> 1; 119 if (str[sa[mid] + i - 1] <= buf[i]) 120 l = mid + 1; 121 else 122 r = mid - 1; 123 } 124 R = l - 1; 125 } 126 127 if (R - L + 1 < K) 128 puts("-1"); 129 // continue; 130 else { 131 int res = 211985, lc = R - L + 1; 132 for (int i = L; i <= R; i++) 133 ar[i - L] = sa[i]; 134 radix_sort(ar, lc); 135 for (int i = K - 1; i < lc; i++) 136 res = min(ar[i] - ar[i - K + 1], res); 137 printf("%d ", res + len); 138 } 139 } 140 } 141 142 int main() { 143 init(); 144 build_sa(); 145 solve(); 146 return 0; 147 }
FLOJ Round

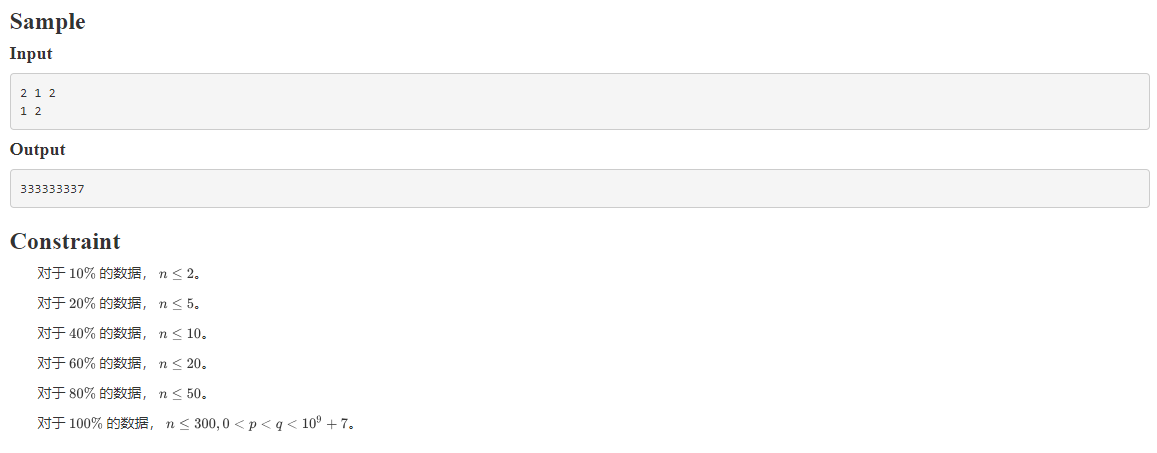
(来自一道多校题)
Solution 1
通过无穷项等比数列求和可以推出第一个选择是第一颗星星的概率。然后可以计算出期望得分。
期望得分10分。
Solution 2
暴力枚举排列计算概率。
期望得分40分。
Solution 3
用$f_{s, i}$表示剩下的星星的集合是$s$,当前走到第$i$个星星。然后概率动态规划,因为转移方程很简单,在环上代入消元解方程。
期望得分60分
Solution 4
考虑如何计算一个排列的字典序排名:

根据期望的线性,答案可以看成两部分相减:一部分是$a_{i} imes (n - i)!$,另一部分是以最终排列以$i$结尾的“正序对”的个数乘$(n - i)!$的期望。
设$dp_{n, i, j}$表示还剩下$n$个星星,考虑到倒数第$n$轮,第$i$个星星在倒数第$j$轮被删掉的概率。
转移的时候考虑当前的$1$是否被拿走。如果它没有被拿走就把环转动一圈,使$i$变为$i - 1$。
如果$1$被拿走,那么还剩下$n - 1$个星星,$i$变为$i - 1$。
因此当$n eq j$的时候可以写成以下转移:(为了方便,假设$1 - 1 = n$)
$dp_{n, i, j} = left (1 - frac{p}{q} ight)dp_{n, i - 1, j} + frac{p}{q}dp_{n - 1, i - 1, j} imes [i eq 1]$
如果$n = j$,那么有:
$dp_{n, i, n} = left (1 - frac{p}{q} ight)dp_{n, i - 1, n} + frac{p}{q} imes [i = 1]$
对于后一部分,由于每个位置被选与它上面的数无关,因此可以考虑设$dp_{n, i, d, j}$表示还剩$n$个星星,第$i$个星星在它后面的第$d$颗星星被拿走前的倒数第$j$轮被拿走的概率。转移类似于上面。
时间复杂度$O(n^4)$,期望得分80分。
Solution 5
注意到对于$dp_{n, i, *}$都有相似的转移,考虑设$f_{n, i} = sum_{dp_{n, i, j} imes (j - 1)!}$,然后可以一起转移了。
对于第二个dp同理。于是时间复杂度成功降为$O(n^3)$。
Code

1 #include <bits/stdc++.h> 2 using namespace std; 3 typedef bool boolean; 4 5 const int N = 305, M = 1e9 + 7; 6 7 void exgcd(int a, int b, int& x, int& y) { 8 if (!b) 9 x = 1, y = 0; 10 else { 11 exgcd(b, a % b, y, x); 12 y -= (a / b) * x; 13 } 14 } 15 16 int inv(int a, int n) { 17 int x, y; 18 exgcd(a, n, x, y); 19 return (x < 0) ? (x + n) : (x); 20 } 21 22 int sub(int a, int b) { 23 a -= b; 24 if (a < 0) 25 return a + M; 26 return a; 27 } 28 29 int n, Pg, Pl; 30 int ar[N], jc[N]; 31 int f[N][N], g[N][N][N]; 32 33 inline void init() { 34 scanf("%d%d%d", &n, &Pg, &Pl); 35 Pg = Pg * 1ll * inv(Pl, M) % M, Pl = sub(1, Pg); 36 for (int i = 1; i <= n; i++) 37 scanf("%d", ar + i), ar[i]--; 38 jc[0] = 1; 39 for (int i = 1; i <= n; i++) 40 jc[i] = jc[i - 1] * 1ll * i % M; 41 } 42 43 int res = 1; 44 inline void solve() { 45 for (int rest = 1; rest <= n; rest++) { 46 int a = 1, b = jc[rest - 1]; 47 for (int i = rest; i > 1; i--) { 48 a = a * 1ll * Pl % M; 49 b = (b + f[rest - 1][i - 1] * 1ll * a) % M; 50 } 51 b = b * 1ll * Pg % M; 52 a = sub(1, a * 1ll * Pl % M); 53 f[rest][1] = b * 1ll * inv(a, M) % M; 54 for (int i = 2; i <= rest; i++) 55 f[rest][i] = (Pl * 1ll * f[rest][i - 1] + Pg * 1ll * f[rest - 1][i - 1]) % M; 56 } 57 58 for (int i = 1; i <= n; i++) 59 res = (res + ar[i] * 1ll * f[n][i]) % M; 60 61 for (int rest = 1; rest <= n; rest++) 62 for (int diff = 1; diff < rest; diff++) { 63 // i is obtained after i + diff in reverse order. 64 // And i is obtained at turn k. 65 int a = 1, b = f[rest - 1][diff]; 66 for (int i = rest; i > 1; i--) { 67 a = a * 1ll * Pl % M; 68 if (i + diff != rest + 1) 69 b = (b + g[rest - 1][diff - (i + diff > rest)][i - 1] * 1ll * a) % M; 70 } 71 a = sub(1, a * 1ll * Pl % M); 72 b = b * 1ll * Pg % M; 73 g[rest][diff][1] = b * 1ll * inv(a, M) % M; 74 for (int i = 2; i <= rest; i++) { 75 g[rest][diff][i] = Pl * 1ll * g[rest][diff][i - 1] % M; 76 if (i + diff != rest + 1) 77 g[rest][diff][i] = (g[rest][diff][i] + Pg * 1ll * g[rest - 1][diff - (i + diff > rest)][i - 1]) % M; 78 } 79 } 80 81 for (int i = 1; i <= n; i++) 82 for (int diff = 1; diff < n; diff++) { 83 int j = i + diff; 84 if (j > n) 85 j -= n; 86 if (ar[i] < ar[j]) 87 res = sub(res, g[n][diff][i]); 88 } 89 printf("%d", res); 90 } 91 92 int main() { 93 init(); 94 solve(); 95 return 0; 96 }
