Watchmen are in a danger and Doctor Manhattan together with his friend Daniel Dreiberg should warn them as soon as possible. There are n watchmen on a plane, the i-th watchman is located at point (xi, yi).
They need to arrange a plan, but there are some difficulties on their way. As you know, Doctor Manhattan considers the distance between watchmen i and j to be |xi - xj| + |yi - yj|. Daniel, as an ordinary person, calculates the distance using the formula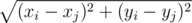 
.
The success of the operation relies on the number of pairs (i, j) (1 ≤ i < j ≤ n), such that the distance between watchman i and watchmen j calculated by Doctor Manhattan is equal to the distance between them calculated by Daniel. You were asked to compute the number of such pairs.
The first line of the input contains the single integer n (1 ≤ n ≤ 200 000) — the number of watchmen.
Each of the following n lines contains two integers xi and yi (|xi|, |yi| ≤ 109).
Some positions may coincide.
Print the number of pairs of watchmen such that the distance between them calculated by Doctor Manhattan is equal to the distance calculated by Daniel.
3
1 1
7 5
1 5
2
6
0 0
0 1
0 2
-1 1
0 1
1 1
11
In the first sample, the distance between watchman 1 and watchman 2 is equal to |1 - 7| + |1 - 5| = 10 for Doctor Manhattan and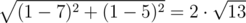 
for Daniel. For pairs (1, 1), (1, 5) and (7, 5), (1, 5)Doctor Manhattan and Daniel will calculate the same distances.
1 #include <cstdio> 2 #include <algorithm> 3 using namespace std; 4 struct Node 5 { 6 int x; 7 int y; 8 }a[200005]; 9 int cmp1(Node a,Node b) 10 { 11 if(a.x==b.x) 12 return a.y<b.y; 13 return a.x<b.x; 14 } 15 int cmp2(Node a,Node b) 16 { 17 if(a.y==b.y) 18 return a.x<b.x; 19 return a.y<b.y; 20 } 21 int main() 22 { 23 int n,i,j; 24 long long ans,cnt,sum; 25 while(~scanf("%d",&n)) 26 { 27 for(i=0;i<n;i++) 28 scanf("%d%d",&a[i].x,&a[i].y); 29 ans=1; 30 cnt=1; 31 sum=0; 32 sort(a,a+n,cmp1); //第一次求对数 33 for(i=1;i<n;i++) 34 { 35 if(a[i].x==a[i-1].x) 36 { 37 ans++; 38 if(a[i].y==a[i-1].y)//重复的对数 39 { 40 cnt++; 41 } 42 else 43 { 44 sum-=cnt*(cnt-1)/2; 45 cnt=1; 46 } 47 } 48 else 49 { 50 sum+=ans*(ans-1)/2; 51 sum-=cnt*(cnt-1)/2; 52 cnt=1; 53 ans=1; 54 } 55 } 56 if(ans!=1) 57 sum+=ans*(ans-1)/2; 58 if(cnt!=1) 59 sum-=cnt*(cnt-1)/2; 60 sort(a,a+n,cmp2);//第二次求对数 61 ans=1; 62 for(i=1;i<n;i++) 63 { 64 if(a[i].y==a[i-1].y) 65 { 66 ans++; 67 } 68 else 69 { 70 sum+=ans*(ans-1)/2; 71 ans=1; 72 } 73 } 74 if(ans!=1) 75 { 76 sum+=ans*(ans-1)/2; 77 } 78 printf("%lld ",sum); 79 } 80 return 0; 81 }