一、数据的预处理
1994年Ronny Kohavi和Barry Becker针对美国某区域的居民做了一次人口普查,经过筛选,一共得到32 561条样本数据。数据中主要包含了关于居民的基本信息以及对应的年收入,其中年收入就是本章中需要预测的变量,具体数据指标和含义见下表:
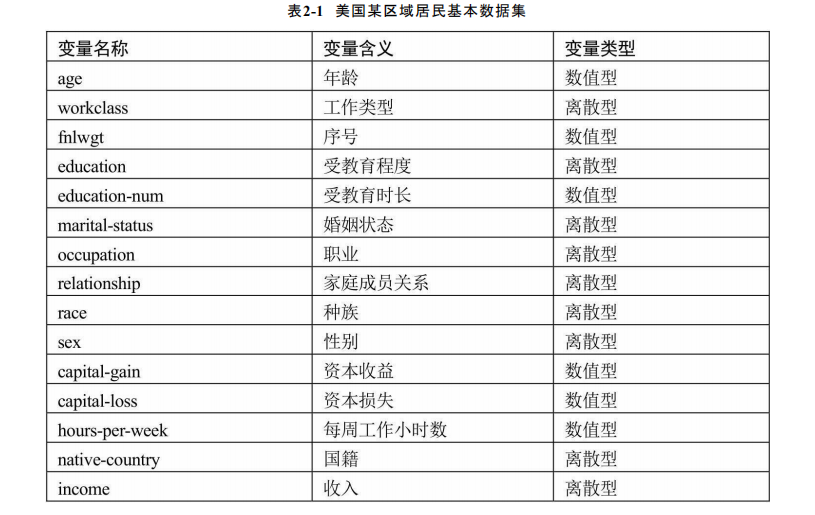
基于上面的数据集,需要预测居民的年收入是否会超过5万美元,从表2-1的变量描述信息可知,有许多变量都是离散型的,如受教育程度、婚姻状态、职业、性别等。通常数据拿到手后,都需要对其进行清洗,例如检查数据中是否存在重复观测、缺失值、异常值等。
1 # -*- coding:utf-8 -*- 2 import pandas as pd 3 import numpy as np 4 import seaborn as sns 5 # 读取数据文件 6 income = pd.read_excel(r"C:UserslenovoDesktopincome.xlsx") 7 8 # 查看数据集是否存在缺失值 9 TJ = income.apply(lambda x:np.sum(x.isnull())) 10 print(TJ)
输出结果为
age 0 workclass 1836 fnlwgt 0 education 0 education-num 0 marital-status 0 occupation 1843 relationship 0 race 0 sex 0 capital-gain 0 capital-loss 0 hours-per-week 0 native-country 583 income 0 dtype: int64
居民的收入数据集中有3个变量存在数值缺失,分别是居民的工作类型、职业和国籍。缺失值的存在一般都会影响分析或建模的结果,所以需要对缺失数值做相应的处理。
处理有三种方式:
一是删除法,即将存在缺失的观测进行删除,如果缺失比例非常小,则删除法是比较合理的,反之,删除比例比较大的缺失值将会丢失一些有用的信息;
二是替换法,即使用一个常数对某个变量的缺失值进行替换,如果缺失的变量是离散型,则可以考虑用众数替换缺失值,如果缺失的变量是数值型,则可以考虑使用均值或中位数替换缺失值;
三是插补法,即运用模型方法,基于未缺失的变量预测缺失变量的值,如常见的回归插补法、多重插补法、拉格朗日插补法等。
由于收入数据集中的3个缺失变量都是离散型变量,这里不妨使用各自的众数来替换缺失值。
1 # 缺失值处理 2 income.fillna(value={"workclass":income.workclass.mode()[0], 3 "occupation":income.occupation.mode()[0], 4 "native-country":income["native-country"].mode()[0]}, 5 inplace=True) 6 TJ = income.apply(lambda x:np.sum(x.isnull())) 7 print(TJ)
经过缺失值处理后可以看到已经没有缺失值了
age 0 workclass 0 fnlwgt 0 education 0 education-num 0 marital-status 0 occupation 0 relationship 0 race 0 sex 0 capital-gain 0 capital-loss 0 hours-per-week 0 native-country 0 income 0 dtype: int64
二、数据的探索性分析
目的是了解数据背后的特征,如数据的集中趋势、离散趋势、数据形状和变量间的关系等。
首先,需要知道每个变量的基本统计值,如均值、中位数、众数等,只有了解了所需处理的数据特征,才能做到“心中有数”。
1 # 数值型变量统计描述 2 d = income.describe() 3 print(d)
可以看到数值型的统计描述
age fnlwgt ... capital-loss hours-per-week count 32561.000000 3.256100e+04 ... 32561.000000 32561.000000 mean 38.581647 1.897784e+05 ... 87.303830 40.437456 std 13.640433 1.055500e+05 ... 402.960219 12.347429 min 17.000000 1.228500e+04 ... 0.000000 1.000000 25% 28.000000 1.178270e+05 ... 0.000000 40.000000 50% 37.000000 1.783560e+05 ... 0.000000 40.000000 75% 48.000000 2.370510e+05 ... 0.000000 45.000000 max 90.000000 1.484705e+06 ... 4356.000000 99.000000
其中包括非缺失观测的个数(count)、平均值(mean)、标准差(std)、最小值(min)、下四分位数(25%)、中位数(50%)、上四分位数(75%)和最大值(max)。
# 离散变量的统计描述 e = income.describe(include=["object"]) print(e)
离散型变量的统计描述如下:
workclass education marital-status ... sex native-country income count 32561 32561 32561 ... 32561 32561 32561 unique 8 16 7 ... 2 41 2 top Private HS-grad Married-civ-spouse ... Male United-States <=50K freq 24532 10501 14976 ... 21790 29753 24720
其中描述当中包含每个变量非缺失观测的数量(count)、不同离散值的个数(unique)、出现频次最高的离散值(top)和最高频次数(freq)。例如:以受教育水平变量为例,一共有16种不同的教育水平;3万多居民中,高中毕业的学历是出现最多的,一共有10 501名。
以被调查居民的年龄和每周工作小时数为例,绘制各自的分布形状图
1 # 导入可视化模块 2 import matplotlib.pyplot as plt 3 4 # 设置绘图风格 5 plt.style.use("ggplot") 6 7 # 设置多图形组合 8 fig,axes = plt.subplots(2,1) 9 10 # 绘制不同收入下年龄的核密度图 11 income.age[income.income == ' <=50K'].plot(kind = 'kde', label = '<=50K', ax = axes[0], legend = True, linestyle = '-') 12 income.age[income.income == ' >50K'].plot(kind = 'kde', label = '>50K', ax = axes[0], legend = True, linestyle = '--') 13 14 # 绘制不同收入水平下的周工作小时数和密度图 15 income['hours-per-week'][income.income == ' <=50K'].plot(kind = 'kde', label = '<=50K', ax = axes[1], legend = True, linestyle = '-') 16 income['hours-per-week'][income.income == ' >50K'].plot(kind = 'kde', label = '>50K', ax = axes[1], legend = True, linestyle = '--') 17 18 # 显示图形 19 plt.show()
结果如下
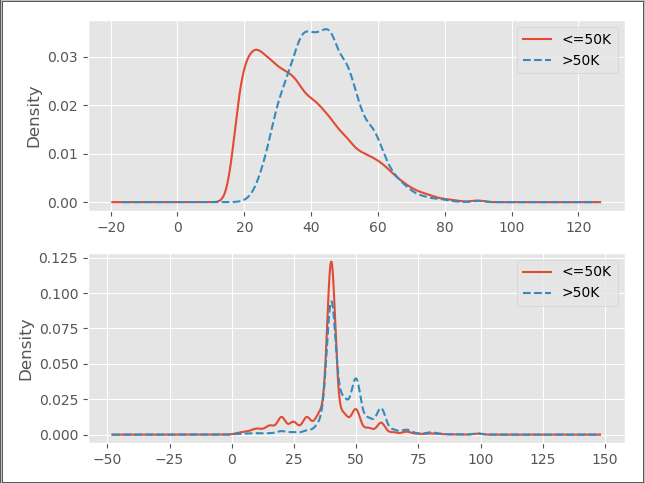
第一幅图展现的是,在不同收入水平下,年龄的核密度分布图,对于年收入超过5万美元的居民来说,他们的年龄几乎呈现正态分布,而收入低于5万美元的居民,年龄呈现右偏特征,即年龄偏大的居民人数要比年龄偏小的人数多;第二幅图展现了不同收入水平下,周工作小时数的核密度图,很明显,两者的分布趋势非常相似,并且出现局部峰值。
下面将不同收入水平下各种族人数的数据和不同收入水平下各家庭关系人数的数据进行分析
1 # 构造不同收入水平下各种族人数的数据 2 race = pd.DataFrame(income.groupby(by = ['race','income']).aggregate(np.size).loc[:,'age']) 3 race = race.reset_index() # 重设行索引 4 race.rename(columns={'age':'counts'}, inplace=True) # 变量重命名,将age更换为counts 5 race.sort_values(by = ['race','counts'], ascending=False, inplace=True) # 排序 6 plt.figure(figsize=(9,5)) # 创建画布 7 # x轴为race,y轴为counts,hue = 'income'按照列名中的值分类形成分类的条形图 8 sns.barplot(x="race", y="counts", hue = 'income', data=race) 9 plt.show() 10 11 # 构造不同收入水平下各家庭关系人数的数据 12 relationship = pd.DataFrame(income.groupby(by = ['relationship','income']).aggregate(np.size).loc[:,'age']) 13 relationship = relationship.reset_index() 14 relationship.rename(columns={'age':'counts'}, inplace=True) 15 relationship.sort_values(by = ['relationship','counts'], ascending=False, inplace=True) 16 plt.figure(figsize=(9,5)) 17 sns.barplot(x="relationship", y="counts", hue = 'income', data=relationship) 18 plt.show()
结果如下:
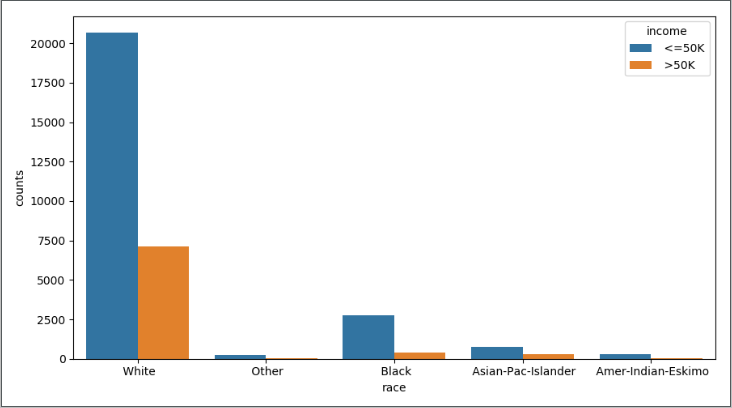
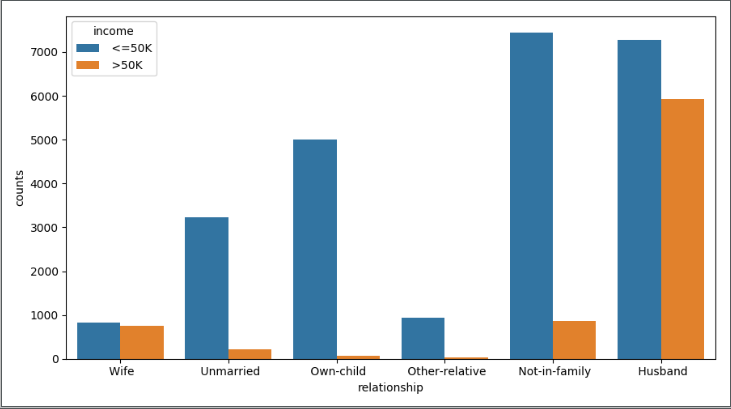
上图反映的是相同的种族下,居民年收入水平高低的人数差异;下图反映的是相同的家庭成员关系下,居民年收入水平高低的人数差异。无论怎么比较,都发现一个规律,即在某一个相同的水平下(如白种人或未结婚人群中),年收入低于5万美元的人数都要比年收入高于5万美元的人数多,这个应该是抽样导致的差异(数据集中年收入低于5万和高于5万的居民比例大致在75%:25%)。
三、数据建模
1、对离散变量进行编码
前面提到,由于收入数据集中有很多离散型变量,这样的字符变量是不能直接用于建模的,需要对这些变量进行重编码,关于重编码的方法有多种,如将字符型的值转换为整数型的值、哑变量处理(0-1变量)、One-Hot热编码(类似于哑变量)等。在本案例中,将采用“字符转数值”的方法对离散型变量进行重编码。
1 # 离散变量的重编码 2 for feature in income.columns: 3 if income[feature].dtype == 'object': 4 income[feature] = pd.Categorical(income[feature]).codes 5 print(income.head())
结果如下
age workclass fnlwgt ... hours-per-week native-country income 0 39 6 77516 ... 40 38 0 1 50 5 83311 ... 13 38 0 2 38 3 215646 ... 40 38 0 3 53 3 234721 ... 40 38 0 4 28 3 338409 ... 40 4 0
[5 rows x 15 columns]
上面的结果就是对字符型离散变量的重编码效果,所有的字符型变量都变成了整数型变量,如workclass、education、marital-status等,接下来就基于这个处理好的数据集对收入水平income进行预测。
在原本的居民收入数据集中,关于受教育程度的有两个变量,一个是education(教育水平),另一个是education-num(受教育时长),而且这两个变量的值都是一一对应的,只不过一个是字符型,另一个是对应的数值型,如果将这两个变量都包含在模型中的话,就会产生信息的冗余。其中该文件当中有fnlwgt变量代表的是一种序号,其对收入水平的高低并没有实际意义。
故为了避免冗余信息和无意义变量对模型的影响,考虑将education变量和fnlwgt变量从数据集中删除。
1 # 删除冗余变量 2 income.drop(["education","fnlwgt"],axis=1,inplace=True) 3 print(income.head())
结果如下
age workclass education-num ... hours-per-week native-country income 0 39 6 13 ... 40 38 0 1 50 5 13 ... 13 38 0 2 38 3 9 ... 40 38 0 3 53 3 7 ... 40 38 0 4 28 3 13 ... 40 4 0
[5 rows x 13 columns]
上面就是经处理“干净”的数据集,所要预测的变量就是income,该变量是二元变量,对其预测的实质就是对年收入水平的分类(一个新样本进来,通过分类模型,可以将该样本分为哪一种收入水平)
关于分类模型有很多种,如Logistic模型、决策树、K近邻、朴素贝叶斯模型、支持向量机、随机森林、梯度提升树GBDT模型等。本案例将对比使用K近邻和GBDT两种分类器,因为通常情况下,都会选用多个模型作为备选,通过对比才能得知哪种模型可以更好地拟合数据。
2、拆分数据集
基于上面的“干净”数据集,需要将其拆分为两个部分,一部分用于分类器模型的构建,另一部分用于分类器模型的评估,这样做的目的是避免分类器模型过拟合或欠拟合。如果模型在训练集上表现很好,而在测试集中表现很差,则说明分类器模型属于过拟合状态;如果模型在训练过程中都不能很好地拟合数据,那说明模型属于欠拟合状态。通常情况下,会把训练集和测试集的比例分配为75%和25%。
1 # 数据拆分 2 # 导入sklearn包 3 from sklearn.model_selection import train_test_split 4 X_train,X_test,y_train,y_test = train_test_split( 5 income.loc[:,"age":"native-country"], # 表示从第一行到最后一行第一列到最后一列 6 income["income"], # 7 train_size=0.75, # 训练长度为75% 8 test_size=0.25, # 测试长度为25% 9 random_state=1234) # 随机种子 10 print("训练数据集共有%d条观测"%X_train.shape[0]) 11 print("测试数据集共有%d条观测"%X_test.shape[0])
输出结果为:
训练数据集共有24420条观测
测试数据集共有8141条观测
结果显示,运用随机抽样的方法,将数据集拆分为两部分,其中训练数据集包含24 420条样本,测试数据集包含8 141条样本,下面将运用拆分好的训练数据集开始构建K近邻和GBDT两种分类器。
3、默认参数的模型构建
1 # 导入K近邻模型类 2 from sklearn.neighbors import KNeighborsClassifier 3 4 # 构建K近邻模型 5 kn = KNeighborsClassifier() 6 kn.fit(X_train,y_train) 7 print(kn)
输出结果为
KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski', metric_params=None, n_jobs=None, n_neighbors=5, p=2, weights='uniform')
首先,针对K近邻模型,这里直接调用sklearn子模块neighbors中的KNeighborsClassifier类,并且使用模型的默认参数,即让K近邻模型自动挑选最佳的搜寻近邻算法(algorithm='auto')、使用欧氏距离公式计算样本间的距离(p=2)、指定未知分类样本的近邻个数5(n_neighbors=5)而且所有近邻样本的权重都相等(weights='uniform')。
# 导入GBDT模型类 from sklearn.ensemble import GradientBoostingClassifier # 构建GBDT模型 gbdt = GradientBoostingClassifier() gbdt.fit(X_train,y_train) print(gbdt)
输出结果为:
GradientBoostingClassifier(criterion='friedman_mse', init=None, learning_rate=0.1, loss='deviance', max_depth=3, max_features=None, max_leaf_nodes=None, min_impurity_decrease=0.0, min_impurity_split=None, min_samples_leaf=1, min_samples_split=2, min_weight_fraction_leaf=0.0, n_estimators=100, n_iter_no_change=None, presort='auto', random_state=None, subsample=1.0, tol=0.0001, validation_fraction=0.1, verbose=0, warm_start=False)
其次,针对GBDT模型,可以调用sklearn子模块ensemble中的GradientBoostingClassifier类,同样先尝试使用该模型的默认参数,即让模型的学习率(迭代步长)为0.1(learning_rate=0.1)、损失函数使用的是对数损失函数(loss='deviance')、生成100棵基础决策树(n_estimators=100),并且每棵基础决策树的最大深度为3(max_depth=3),中间节点(非叶节点)的最小样本量为2(min_samples_split=2),叶节点的最小样本量为1(min_samples_leaf=1),每一棵树的训练都不会基于上一棵树的结果(warm_start=False)。
上面的K近邻模型和GBDT模型都是直接调用第三方模块,并且都是基于默认参数的模型构建,虽然这个方法可行,但是往往有时默认参数并不能得到最佳的拟合效果。所以,需要不停地调整模型参数,例如K近邻模型设置不同的K值、GBDT模型中设置不同的学习率、基础决策树的数量、基础决策树的最大深度等。
在Python的sklearn模块中提供了网格搜索法,目的就是找到上面提到的最佳参数。
4、模型网格搜索
同样,先对K近邻模型的参数进行网格搜索,这里仅考虑模型中n_neighbors参数的不同选择。
1 # K近邻模型的网格搜索法 2 # 导入网格搜索法的函数 3 from sklearn.model_selection import GridSearchCV 4 5 # 选择不同的参数 6 k_options = list(range(1,12)) 7 parameters = {"n_neighbors":k_options} 8 9 # 搜索不同的K值 10 # estimator为接收一个模型(这里是K近邻), 11 # param_grid用来指定模型需要搜索的参数列表对象,这里是K近邻模型中n_neighbors参数的11种可能值 12 # cv是指网格搜索需要经过10重交叉验证 13 # scoring指定模型评估的度量值,这里选用的是模型预测的准确率。 14 grid_kn = GridSearchCV(estimator=KNeighborsClassifier(),param_grid=parameters,cv=10,scoring="accuracy",verbose=0) 15 grid_kn.fit(X_train,y_train) 16 print(grid_kn) 17 18 # 输出结果 19 print(grid_kn.grid_scores_,grid_kn.best_params_,grid_kn.best_score_)
结果为
GridSearchCV(cv=10, error_score='raise-deprecating', estimator=KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski', metric_params=None, n_jobs=None, n_neighbors=5, p=2, weights='uniform'), fit_params=None, iid='warn', n_jobs=None, param_grid={'n_neighbors': [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]}, pre_dispatch='2*n_jobs', refit=True, return_train_score='warn', scoring='accuracy', verbose=0)
{'mean_fit_time': array([3.67050991, 3.49790006, 2.75365753, 2.84446259, 2.8229614 , 2.90116584, 2.91606674, 3.59870582, 3.53100197, 4.00322902, 3.47259858]), 'std_fit_time': array([0.45154768, 0.11045269, 0.29897835, 0.40807748, 0.40795633, 0.41141417, 0.37407101, 0.45431517, 0.53144257, 0.66446484, 0.72532843]), 'mean_score_time': array([1.43008177, 1.43338201, 1.42938178, 1.40888066, 1.43998239, 1.45078299, 1.50678616, 1.78500214, 1.79490266, 1.95031154, 1.66759543]), 'std_score_time': array([0.10384432, 0.04353661, 0.22413559, 0.20598305, 0.1824366 , 0.23036254, 0.22165888, 0.24491901, 0.22654143, 0.28577981, 0.14816731]), 'param_n_neighbors': masked_array(data=[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11], mask=[False, False, False, False, False, False, False, False, False, False, False], fill_value='?', dtype=object), 'params': [{'n_neighbors': 1}, {'n_neighbors': 2}, {'n_neighbors': 3}, {'n_neighbors': 4}, {'n_neighbors': 5}, {'n_neighbors': 6}, {'n_neighbors': 7}, {'n_neighbors': 8}, {'n_neighbors': 9}, {'n_neighbors': 10}, {'n_neighbors': 11}], 'split0_test_score': array([0.8014736 , 0.82316824, 0.8215309 , 0.8264429 , 0.82889889, 0.83381089, 0.83831355, 0.83503889, 0.83831355, 0.84036021, 0.84322554]), 'split1_test_score': array([0.81416291, 0.83585755, 0.83544822, 0.84936553, 0.84240688, 0.8489562 , 0.84527221, 0.84486287, 0.84240688, 0.84568154, 0.84117888]), 'split2_test_score': array([0.81866558, 0.83790422, 0.84158821, 0.85550553, 0.84568154, 0.85345886, 0.84854687, 0.85100287, 0.84731887, 0.84854687, 0.84690954]), 'split3_test_score': array([0.81539091, 0.84854687, 0.84936553, 0.84936553, 0.84527221, 0.84977487, 0.84568154, 0.84609087, 0.84240688, 0.84486287, 0.8501842 ]), 'split4_test_score': array([0.80917281, 0.83538084, 0.83701884, 0.84316134, 0.83783784, 0.84111384, 0.83783784, 0.83824734, 0.83619984, 0.83865684, 0.83701884]), 'split5_test_score': array([0.82186732, 0.83783784, 0.83619984, 0.84111384, 0.83210483, 0.84029484, 0.83415233, 0.83947584, 0.84234234, 0.84520885, 0.84316134]), 'split6_test_score': array([0.81810733, 0.8467841 , 0.84104875, 0.85866448, 0.85210979, 0.86112249, 0.85006145, 0.85784515, 0.85210979, 0.85088079, 0.84842278]), 'split7_test_score': array([0.82466202, 0.8455551 , 0.84965178, 0.85538714, 0.85743548, 0.86071282, 0.85907415, 0.85743548, 0.86112249, 0.85948382, 0.85538714]), 'split8_test_score': array([0.8095043 , 0.83408439, 0.8275297 , 0.83490373, 0.83941008, 0.84309709, 0.83900041, 0.83981975, 0.84104875, 0.84350676, 0.84391643]), 'split9_test_score': array([0.81482999, 0.83941008, 0.83039738, 0.83818107, 0.83900041, 0.84473576, 0.84514543, 0.84596477, 0.8443261 , 0.8467841 , 0.84350676]), 'mean_test_score': array([0.81478296, 0.83845209, 0.83697789, 0.84520885, 0.84201474, 0.8477068 , 0.84430794, 0.8455774 , 0.84475839, 0.8463964 , 0.84529075]), 'std_test_score': array([0.00641223, 0.00701638, 0.00852103, 0.00976708, 0.00816947, 0.00842365, 0.00694003, 0.00746034, 0.00688403, 0.00552323, 0.00487327]), 'rank_test_score': array([11, 9, 10, 5, 8, 1, 7, 3, 6, 2, 4]), 'split0_train_score': array([0.97743095, 0.91049734, 0.90571962, 0.8947081 , 0.89175047, 0.88351458, 0.88242253, 0.87805433, 0.87577922, 0.87241207, 0.87045548]), 'split1_train_score': array([0.97606589, 0.90672066, 0.90521909, 0.89266051, 0.88897484, 0.88196751, 0.8816945 , 0.87687127, 0.8752787 , 0.87186604, 0.87054648]), 'split2_train_score': array([0.97574737, 0.90713018, 0.90499158, 0.89074942, 0.88838331, 0.88105747, 0.87791782, 0.87605224, 0.8731856 , 0.87068299, 0.86918142]), 'split3_train_score': array([0.97611139, 0.9076307 , 0.90444556, 0.88979388, 0.88952086, 0.88092096, 0.8796014 , 0.87659826, 0.87391364, 0.87009146, 0.87059198]), 'split4_train_score': array([0.97520248, 0.90895441, 0.90604241, 0.89371189, 0.89029939, 0.88342888, 0.88197288, 0.87623988, 0.87664938, 0.87223587, 0.87146237]), 'split5_train_score': array([0.97647648, 0.90868141, 0.9039494 , 0.89202839, 0.88884339, 0.88270088, 0.88051688, 0.87728638, 0.87564838, 0.87228137, 0.87109837]), 'split6_train_score': array([0.97588607, 0.90709313, 0.90545521, 0.89130534, 0.88812048, 0.88170526, 0.87993084, 0.8764275 , 0.8741071 , 0.87042177, 0.86796488]), 'split7_train_score': array([0.97606806, 0.90759361, 0.90449975, 0.89039538, 0.88734701, 0.88034032, 0.87811092, 0.87519905, 0.87215069, 0.87023977, 0.86892033]), 'split8_train_score': array([0.97606806, 0.90800309, 0.90445425, 0.89326175, 0.88971291, 0.88393466, 0.88143228, 0.87788343, 0.87610901, 0.87274216, 0.86996679]), 'split9_train_score': array([0.97584058, 0.90877656, 0.90486373, 0.89253378, 0.89025888, 0.88379817, 0.88193275, 0.87806543, 0.87478957, 0.87260567, 0.87092224]), 'mean_train_score': array([0.97608973, 0.90810811, 0.90496406, 0.89211484, 0.88932115, 0.88233687, 0.88055328, 0.87686778, 0.87476113, 0.87155792, 0.87011103]), 'std_train_score': array([0.00054391, 0.00107774, 0.00061844, 0.00148104, 0.00120407, 0.00124754, 0.00153925, 0.0009033 , 0.00133856, 0.00101253, 0.00104438])}
{'n_neighbors': 6}
0.8477067977067977
通过网格搜索的计算,得到三部分的结果,第一部分包含了11种K值下的平均准确率(因为做了10重交叉验证);第二部分选择出了最佳的K值,K值为6;第三部分是当K值为6时模型的最佳平均准确率,且准确率为84.78%。
接下来,对GBDT模型的参数进行网格搜索,搜索的参数包含三个,分别是模型的学习速率、生成的基础决策树个数和每个基础决策树的最大深度。
1 # GBDT模型的网格搜索法 2 # 选择不同的参数 3 learning_rate_options = [0.01,0.05,0.1] 4 max_depth_options = [3,5,7,9] 5 n_estimators_options = [100,300,500] 6 parameters = {"learning_rate":learning_rate_options, 7 "max_depth":max_depth_options, 8 "n_estimators":n_estimators_options} 9 grid_gbdt = GridSearchCV(estimator=GradientBoostingClassifier(),param_grid=parameters,cv=10,scoring="accuracy") 10 grid_gbdt.fit(X_train,y_train) 11 print(grid_gbdt) 12 print(grid_gbdt.cv_results_,grid_gbdt.best_params_,grid_gbdt.best_score_)
结果如下:

GridSearchCV(cv=10, error_score='raise-deprecating', estimator=GradientBoostingClassifier(criterion='friedman_mse', init=None, learning_rate=0.1, loss='deviance', max_depth=3, max_features=None, max_leaf_nodes=None, min_impurity_decrease=0.0, min_impurity_split=None, min_samples_leaf=1, min_sampl... subsample=1.0, tol=0.0001, validation_fraction=0.1, verbose=0, warm_start=False), fit_params=None, iid='warn', n_jobs=None, param_grid={'learning_rate': [0.01, 0.05, 0.1], 'max_depth': [3, 5, 7, 9], 'n_estimators': [100, 300, 500]}, pre_dispatch='2*n_jobs', refit=True, return_train_score='warn', scoring='accuracy', verbose=0) {'mean_fit_time': array([ 3.22888467, 9.48794255, 15.5971921 , 6.87229314, 21.33582032, 34.87079453, 13.80808976, 44.45444269, 74.51926224, 27.33946373, 95.72927544, 160.67909031, 3.1726815 , 9.09182007, 14.78414559, 7.02700193, 19.38840888, 31.41349676, 14.86094999, 41.79069023, 72.07182229, 32.60806501, 94.35729699, 157.19259093, 3.10537763, 8.82440469, 14.59613488, 6.67568185, 18.84847803, 31.43649802, 14.15780981, 41.44967077, 70.47793109, 29.51588826, 92.89461317, 163.10202885]), 'std_fit_time': array([0.06870769, 0.04685603, 0.06431241, 0.04635014, 0.06956576, 0.11038631, 0.2626879 , 0.33654791, 1.62161041, 1.30857627, 1.95577161, 6.96091192, 0.04830234, 0.05451932, 0.0714128 , 0.05610162, 0.10786263, 0.17567451, 0.10904245, 1.72992668, 2.06189075, 0.89412714, 2.42497891, 7.08472918, 0.05114932, 0.05087226, 0.06361028, 0.05440354, 0.1110245 , 0.17552705, 0.12799712, 0.34807914, 0.50233235, 0.39280175, 0.71967804, 1.49674555]), 'mean_score_time': array([0.01190069, 0.02720163, 0.04130239, 0.01620088, 0.04030232, 0.06250358, 0.02020113, 0.05490315, 0.08480482, 0.02680159, 0.07490432, 0.12100697, 0.01140068, 0.02470133, 0.03640206, 0.01640093, 0.03590207, 0.05380309, 0.02050118, 0.04850278, 0.07850444, 0.02710161, 0.0657037 , 0.10800617, 0.01110065, 0.02330139, 0.03560202, 0.01480076, 0.03450198, 0.05450311, 0.01950109, 0.04820282, 0.07880447, 0.02490141, 0.06690388, 0.11180637]), 'std_score_time': array([0.00053854, 0.00146981, 0.00110012, 0.00116618, 0.00110012, 0.00233462, 0.00040004, 0.00175795, 0.00183313, 0.00116618, 0.00378049, 0.0081736 , 0.0004899 , 0.00078101, 0.00142844, 0.00091662, 0.00151344, 0.00116626, 0.00080629, 0.00143191, 0.00237708, 0.00122068, 0.0013454 , 0.00402513, 0.00083069, 0.00078113, 0.00120018, 0.00039999, 0.00102481, 0.0016883 , 0.0008063 , 0.00213558, 0.00285678, 0.00053863, 0.00250807, 0.00442293]), 'param_learning_rate': masked_array(data=[0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.05, 0.05, 0.05, 0.05, 0.05, 0.05, 0.05, 0.05, 0.05, 0.05, 0.05, 0.05, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1], mask=[False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False], fill_value='?', dtype=object), 'param_max_depth': masked_array(data=[3, 3, 3, 5, 5, 5, 7, 7, 7, 9, 9, 9, 3, 3, 3, 5, 5, 5, 7, 7, 7, 9, 9, 9, 3, 3, 3, 5, 5, 5, 7, 7, 7, 9, 9, 9], mask=[False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False], fill_value='?', dtype=object), 'param_n_estimators': masked_array(data=[100, 300, 500, 100, 300, 500, 100, 300, 500, 100, 300, 500, 100, 300, 500, 100, 300, 500, 100, 300, 500, 100, 300, 500, 100, 300, 500, 100, 300, 500, 100, 300, 500, 100, 300, 500], mask=[False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False], fill_value='?', dtype=object), 'params': [{'learning_rate': 0.01, 'max_depth': 3, 'n_estimators': 100}, {'learning_rate': 0.01, 'max_depth': 3, 'n_estimators': 300}, {'learning_rate': 0.01, 'max_depth': 3, 'n_estimators': 500}, {'learning_rate': 0.01, 'max_depth': 5, 'n_estimators': 100}, {'learning_rate': 0.01, 'max_depth': 5, 'n_estimators': 300}, {'learning_rate': 0.01, 'max_depth': 5, 'n_estimators': 500}, {'learning_rate': 0.01, 'max_depth': 7, 'n_estimators': 100}, {'learning_rate': 0.01, 'max_depth': 7, 'n_estimators': 300}, {'learning_rate': 0.01, 'max_depth': 7, 'n_estimators': 500}, {'learning_rate': 0.01, 'max_depth': 9, 'n_estimators': 100}, {'learning_rate': 0.01, 'max_depth': 9, 'n_estimators': 300}, {'learning_rate': 0.01, 'max_depth': 9, 'n_estimators': 500}, {'learning_rate': 0.05, 'max_depth': 3, 'n_estimators': 100}, {'learning_rate': 0.05, 'max_depth': 3, 'n_estimators': 300}, {'learning_rate': 0.05, 'max_depth': 3, 'n_estimators': 500}, {'learning_rate': 0.05, 'max_depth': 5, 'n_estimators': 100}, {'learning_rate': 0.05, 'max_depth': 5, 'n_estimators': 300}, {'learning_rate': 0.05, 'max_depth': 5, 'n_estimators': 500}, {'learning_rate': 0.05, 'max_depth': 7, 'n_estimators': 100}, {'learning_rate': 0.05, 'max_depth': 7, 'n_estimators': 300}, {'learning_rate': 0.05, 'max_depth': 7, 'n_estimators': 500}, {'learning_rate': 0.05, 'max_depth': 9, 'n_estimators': 100}, {'learning_rate': 0.05, 'max_depth': 9, 'n_estimators': 300}, {'learning_rate': 0.05, 'max_depth': 9, 'n_estimators': 500}, {'learning_rate': 0.1, 'max_depth': 3, 'n_estimators': 100}, {'learning_rate': 0.1, 'max_depth': 3, 'n_estimators': 300}, {'learning_rate': 0.1, 'max_depth': 3, 'n_estimators': 500}, {'learning_rate': 0.1, 'max_depth': 5, 'n_estimators': 100}, {'learning_rate': 0.1, 'max_depth': 5, 'n_estimators': 300}, {'learning_rate': 0.1, 'max_depth': 5, 'n_estimators': 500}, {'learning_rate': 0.1, 'max_depth': 7, 'n_estimators': 100}, {'learning_rate': 0.1, 'max_depth': 7, 'n_estimators': 300}, {'learning_rate': 0.1, 'max_depth': 7, 'n_estimators': 500}, {'learning_rate': 0.1, 'max_depth': 9, 'n_estimators': 100}, {'learning_rate': 0.1, 'max_depth': 9, 'n_estimators': 300}, {'learning_rate': 0.1, 'max_depth': 9, 'n_estimators': 500}], 'split0_test_score': array([0.82685223, 0.83422022, 0.84404421, 0.83381089, 0.84445354, 0.85100287, 0.83667622, 0.8465002 , 0.84854687, 0.83422022, 0.84322554, 0.84199754, 0.84322554, 0.8514122 , 0.85427753, 0.85304953, 0.85386819, 0.85509619, 0.84731887, 0.8501842 , 0.84936553, 0.84281621, 0.83954155, 0.83503889, 0.8489562 , 0.85345886, 0.85059353, 0.85304953, 0.8501842 , 0.85223086, 0.85386819, 0.84281621, 0.83790422, 0.84445354, 0.83258289, 0.82562423]), 'split1_test_score': array([0.85304953, 0.86614818, 0.86860418, 0.86410151, 0.8714695 , 0.8726975 , 0.86410151, 0.87556283, 0.87883749, 0.85959885, 0.8739255 , 0.8763815 , 0.86901351, 0.87228817, 0.87679083, 0.87474417, 0.87924683, 0.88088416, 0.87842816, 0.88129349, 0.87720016, 0.8739255 , 0.87801883, 0.87187884, 0.86778551, 0.87965616, 0.88252149, 0.87679083, 0.87679083, 0.87801883, 0.88047483, 0.87679083, 0.87024151, 0.8739255 , 0.86369218, 0.85837086]), 'split2_test_score': array([0.84486287, 0.85714286, 0.86369218, 0.84977487, 0.86942284, 0.87187884, 0.85509619, 0.8751535 , 0.8763815 , 0.85304953, 0.87310684, 0.87965616, 0.86369218, 0.87474417, 0.8763815 , 0.87187884, 0.87679083, 0.87597217, 0.87433483, 0.87474417, 0.87351617, 0.8776095 , 0.87106017, 0.86532951, 0.86983217, 0.87679083, 0.87679083, 0.87351617, 0.87679083, 0.87187884, 0.87842816, 0.87187884, 0.86860418, 0.87597217, 0.86082685, 0.85796152]), 'split3_test_score': array([0.83872288, 0.85509619, 0.86287352, 0.84527221, 0.87024151, 0.8776095 , 0.85468686, 0.88006549, 0.88538682, 0.85918952, 0.87556283, 0.87924683, 0.86369218, 0.87228817, 0.8763815 , 0.87801883, 0.88415882, 0.88620549, 0.88334016, 0.88374949, 0.88293082, 0.87965616, 0.88088416, 0.86942284, 0.87065084, 0.8763815 , 0.88129349, 0.88252149, 0.88497749, 0.88129349, 0.88497749, 0.88129349, 0.8714695 , 0.87965616, 0.86246418, 0.86082685]), 'split4_test_score': array([0.85176085, 0.86322686, 0.86895987, 0.86076986, 0.86895987, 0.87755938, 0.85995086, 0.87223587, 0.87510238, 0.85462735, 0.87264537, 0.87182637, 0.86936937, 0.87510238, 0.87510238, 0.87919738, 0.87633088, 0.87346437, 0.87592138, 0.87387387, 0.87223587, 0.87100737, 0.86363636, 0.85380835, 0.87469287, 0.87428337, 0.87264537, 0.87633088, 0.87305487, 0.87387387, 0.87428337, 0.87223587, 0.85954136, 0.86773137, 0.85462735, 0.84684685]), 'split5_test_score': array([0.83701884, 0.84930385, 0.85462735, 0.84930385, 0.85667486, 0.86977887, 0.85012285, 0.86445536, 0.87346437, 0.84930385, 0.87141687, 0.87592138, 0.85421785, 0.86977887, 0.87469287, 0.87100737, 0.87551188, 0.87551188, 0.87510238, 0.87837838, 0.87305487, 0.87469287, 0.87100737, 0.86568387, 0.86445536, 0.87674038, 0.87714988, 0.87305487, 0.87755938, 0.87264537, 0.87755938, 0.87387387, 0.86650287, 0.87141687, 0.85872236, 0.85708436]), 'split6_test_score': array([0.84719377, 0.85702581, 0.8648095 , 0.85661614, 0.86562884, 0.8738222 , 0.85989349, 0.87832855, 0.88529291, 0.85948382, 0.87668988, 0.88037689, 0.8648095 , 0.8738222 , 0.88365424, 0.87546088, 0.88652192, 0.88406391, 0.88324457, 0.88652192, 0.88488324, 0.88242524, 0.87955756, 0.87341254, 0.86972552, 0.88529291, 0.88816059, 0.88447358, 0.88365424, 0.88242524, 0.88897993, 0.87832855, 0.87546088, 0.88406391, 0.86890619, 0.86399017]), 'split7_test_score': array([0.8455551 , 0.85415813, 0.85702581, 0.85620647, 0.86153216, 0.86644818, 0.85702581, 0.87054486, 0.8725932 , 0.85661614, 0.8725932 , 0.8738222 , 0.85702581, 0.86685785, 0.86808685, 0.86685785, 0.87013519, 0.86972552, 0.87546088, 0.87587054, 0.8725932 , 0.87587054, 0.87013519, 0.8635805 , 0.8635805 , 0.86890619, 0.87054486, 0.87013519, 0.87464154, 0.87709955, 0.87668988, 0.8713642 , 0.86030315, 0.87177386, 0.86644818, 0.85661614]), 'split8_test_score': array([0.84104875, 0.85006145, 0.8533388 , 0.84842278, 0.8545678 , 0.85989349, 0.84883245, 0.86030315, 0.86562884, 0.84924211, 0.85866448, 0.8635805 , 0.85374846, 0.86030315, 0.86767718, 0.85948382, 0.86972552, 0.86767718, 0.86685785, 0.8648095 , 0.86317083, 0.86644818, 0.86153216, 0.85620647, 0.85825481, 0.86685785, 0.86726751, 0.86562884, 0.86603851, 0.86808685, 0.8635805 , 0.8635805 , 0.85415813, 0.86153216, 0.85210979, 0.84473576]), 'split9_test_score': array([0.84063908, 0.85292913, 0.85661614, 0.84924211, 0.86071282, 0.86849652, 0.85251946, 0.86931585, 0.87300287, 0.85292913, 0.87054486, 0.87423187, 0.85866448, 0.87054486, 0.87709955, 0.86931585, 0.87832855, 0.87996723, 0.8738222 , 0.87709955, 0.8725932 , 0.8738222 , 0.87709955, 0.86972552, 0.86521917, 0.87546088, 0.87791889, 0.87587054, 0.87791889, 0.87505121, 0.87750922, 0.87054486, 0.86726751, 0.87177386, 0.8635805 , 0.8635805 ]), 'mean_test_score': array([0.84266994, 0.8539312 , 0.85945946, 0.85135135, 0.86236691, 0.86891892, 0.85389025, 0.86924652, 0.87342342, 0.85282555, 0.86883702, 0.87170352, 0.85974611, 0.86871417, 0.87301392, 0.86990172, 0.87506143, 0.87485667, 0.87338247, 0.87465192, 0.87215397, 0.87182637, 0.86924652, 0.86240786, 0.86531532, 0.87338247, 0.87448812, 0.87313677, 0.87416052, 0.87325962, 0.87563473, 0.87027027, 0.86314496, 0.87022932, 0.85839476, 0.85356265]), 'std_test_score': array([0.00727039, 0.00826494, 0.00737996, 0.00816746, 0.00816387, 0.0077901 , 0.00725997, 0.00951581, 0.01002796, 0.00721066, 0.009741 , 0.01093037, 0.0076383 , 0.00712003, 0.00760216, 0.0078359 , 0.0086553 , 0.00864945, 0.0097921 , 0.00992718, 0.00952303, 0.01054302, 0.0116674 , 0.01093596, 0.0069548 , 0.00823344, 0.0098191 , 0.00846626, 0.00942951, 0.00812988, 0.0096227 , 0.01023955, 0.01033708, 0.01039025, 0.00986421, 0.01108992]), 'rank_test_score': array([36, 31, 29, 35, 27, 21, 32, 19, 7, 34, 22, 15, 28, 23, 12, 18, 2, 3, 8, 4, 13, 14, 19, 26, 24, 8, 5, 11, 6, 10, 1, 16, 25, 17, 30, 33]), 'split0_train_score': array([0.84447377, 0.85725986, 0.86394867, 0.85671384, 0.8709105 , 0.87887337, 0.86526823, 0.88583519, 0.89179597, 0.87150202, 0.89748373, 0.90462757, 0.86367566, 0.87678027, 0.88192201, 0.87864586, 0.89188697, 0.89871229, 0.89147745, 0.91090686, 0.92587705, 0.90512809, 0.9377076 , 0.96391682, 0.87186604, 0.88478864, 0.88942986, 0.88792829, 0.90276198, 0.91441052, 0.90248897, 0.93352141, 0.95290531, 0.92455749, 0.96901306, 0.97861401]), 'split1_train_score': array([0.84156163, 0.85352869, 0.86149156, 0.85425672, 0.86686081, 0.87577922, 0.85989899, 0.88224052, 0.89047641, 0.86572326, 0.8946171 , 0.90285298, 0.86121855, 0.8731401 , 0.87910088, 0.87596123, 0.89170496, 0.89962233, 0.88997588, 0.91013332, 0.92501251, 0.903308 , 0.93720708, 0.95991264, 0.86904491, 0.8817855 , 0.88692724, 0.88510716, 0.90189744, 0.91281795, 0.89971334, 0.93233835, 0.95226828, 0.92219138, 0.96728398, 0.97688493]), 'split2_train_score': array([0.84242617, 0.85525777, 0.86144606, 0.85225463, 0.86781635, 0.87514219, 0.86090003, 0.88214952, 0.8882013 , 0.86854439, 0.89434409, 0.90335351, 0.86130955, 0.87418665, 0.8796014 , 0.87559722, 0.88965737, 0.89821177, 0.88838331, 0.90913227, 0.92355645, 0.90408154, 0.93907267, 0.96045866, 0.86858989, 0.88096646, 0.88679074, 0.88406061, 0.90226146, 0.9119079 , 0.90057788, 0.93161032, 0.95167675, 0.92282841, 0.96723848, 0.97756746]), 'split3_train_score': array([0.84420076, 0.85425672, 0.86080903, 0.8494335 , 0.86763434, 0.87573372, 0.85967147, 0.88114847, 0.88833781, 0.86786186, 0.89402557, 0.90153342, 0.86094553, 0.87336761, 0.8794649 , 0.87555171, 0.88911134, 0.89666469, 0.88902034, 0.9075852 , 0.92387496, 0.90271648, 0.93670656, 0.96014015, 0.86849889, 0.88078446, 0.88665423, 0.88442463, 0.89966783, 0.91049734, 0.89839378, 0.93315739, 0.95158575, 0.92432998, 0.96696546, 0.97815898]), 'split4_train_score': array([0.84170534, 0.85444535, 0.86095186, 0.85567386, 0.86841387, 0.87601238, 0.86227136, 0.88306488, 0.89039039, 0.86977887, 0.8956684 , 0.9040404 , 0.86117936, 0.87373737, 0.88119938, 0.87642188, 0.89107289, 0.8980799 , 0.89066339, 0.90959141, 0.92378742, 0.9037219 , 0.93757394, 0.96036946, 0.86827737, 0.88192738, 0.88743289, 0.88638639, 0.9020839 , 0.91359541, 0.9006734 , 0.93120393, 0.95140595, 0.92483392, 0.96678497, 0.97697698]), 'split5_train_score': array([0.84429884, 0.85526436, 0.86258986, 0.85649286, 0.86650287, 0.87605788, 0.86286286, 0.88169988, 0.88888889, 0.86964237, 0.89416689, 0.9030394 , 0.86181636, 0.87401037, 0.87937938, 0.87628538, 0.89002639, 0.8985349 , 0.88879789, 0.90936391, 0.92387842, 0.9036309 , 0.93579944, 0.96055146, 0.86891437, 0.88129038, 0.88638639, 0.88402038, 0.9011284 , 0.91122941, 0.8999909 , 0.93188643, 0.95208845, 0.92292292, 0.96842297, 0.97811448]), 'split6_train_score': array([0.84212203, 0.85454297, 0.86132217, 0.85517994, 0.86714591, 0.87610901, 0.86177715, 0.88238773, 0.88903044, 0.86823786, 0.89344374, 0.90295282, 0.86123118, 0.87301515, 0.87838391, 0.87656399, 0.88921243, 0.89758406, 0.88866645, 0.9078666 , 0.92310842, 0.90222485, 0.9371218 , 0.95891533, 0.86882934, 0.87970335, 0.8852996 , 0.88384367, 0.89958597, 0.91159743, 0.89822103, 0.93170754, 0.95099868, 0.92115201, 0.96651349, 0.97725101]), 'split7_train_score': array([0.8426225 , 0.85517994, 0.86200464, 0.85568042, 0.86696392, 0.87656399, 0.86205014, 0.8830702 , 0.88953092, 0.86914782, 0.89631011, 0.90313481, 0.86218663, 0.87387961, 0.8808408 , 0.87620001, 0.89071386, 0.89726557, 0.88930343, 0.90914054, 0.92406388, 0.90308931, 0.93511989, 0.96032577, 0.86946631, 0.88284271, 0.88793849, 0.8852996 , 0.90263433, 0.91200692, 0.90149688, 0.93289049, 0.95231812, 0.92456436, 0.96774194, 0.97788798]), 'split8_train_score': array([0.8428045 , 0.8561354 , 0.86305109, 0.85713636, 0.86951181, 0.87824742, 0.8628236 , 0.8830702 , 0.89030438, 0.87142272, 0.89681059, 0.90686564, 0.86336958, 0.87560854, 0.88061331, 0.87879339, 0.89171482, 0.89822103, 0.89007689, 0.90868556, 0.92292643, 0.90536421, 0.93812275, 0.96087174, 0.87001228, 0.88343419, 0.88802948, 0.88684654, 0.90258883, 0.91255289, 0.90145139, 0.93302698, 0.955048 , 0.92520133, 0.96792393, 0.97779699]), 'split9_train_score': array([0.84407844, 0.85572592, 0.86232313, 0.85299604, 0.86696392, 0.87665499, 0.86195914, 0.88147777, 0.88925793, 0.86996679, 0.89567314, 0.90231585, 0.86268711, 0.87401611, 0.87915738, 0.87665499, 0.89053187, 0.89681059, 0.89012239, 0.90804859, 0.92379089, 0.90313481, 0.93511989, 0.95918832, 0.86978479, 0.88043132, 0.88743801, 0.88457164, 0.90163338, 0.91337185, 0.90031394, 0.92966013, 0.95231812, 0.92420037, 0.96774194, 0.977433 ]), 'mean_train_score': array([0.8430294 , 0.8551597 , 0.86199381, 0.85458182, 0.86787243, 0.87651742, 0.8619483 , 0.88261444, 0.88962144, 0.8691828 , 0.89525434, 0.90347164, 0.86196195, 0.87417418, 0.87996633, 0.87666757, 0.89056329, 0.89797071, 0.88964874, 0.90904543, 0.92398764, 0.90364001, 0.93695516, 0.96046503, 0.86932842, 0.88179544, 0.88723269, 0.88524889, 0.90162435, 0.91239876, 0.90033215, 0.9321003 , 0.95226134, 0.92367822, 0.96756302, 0.97766858]), 'std_train_score': array([0.0010715 , 0.00100352, 0.00094318, 0.00228083, 0.00131712, 0.0011067 , 0.00152483, 0.00125206, 0.00105868, 0.00163071, 0.00126724, 0.001387 , 0.00093132, 0.00110643, 0.00105664, 0.00108436, 0.00098523, 0.0008618 , 0.00093234, 0.00098537, 0.00082551, 0.0009441 , 0.00122562, 0.0012868 , 0.00099868, 0.00144779, 0.00105447, 0.00130699, 0.00110296, 0.0011245 , 0.0012709 , 0.00108971, 0.00106493, 0.00125684, 0.00072688, 0.00052252])} {'learning_rate': 0.1, 'max_depth': 7, 'n_estimators': 100} 0.8756347256347257
输出的结果与K近邻结构相似,仍然包含三个部分。第一部分包含了11种K值下的平均准确率(因为做了10重交叉验证);第二部分的结果可知,最佳的模型学习率为0.1,生成的基础决策树个数为100棵,并且每棵基础决策树的最大深度为7。这样的组合可以使GBDT模型的平均准确率达到87.56%。
5、模型预测与评估
通常,验证模型好坏的方法有多种。例如,对于预测的连续变量来说,常用的衡量指标有均方误差(MSE)和均方根误差(RMSE);对于预测的分类变量来说,常用的衡量指标有混淆矩阵中的准确率、ROC曲线下的面积AUC、K-S值等。
6、默认的K近邻模型
1 # K近邻模型在测试集上的预测 2 kn_pred = kn.predict(X_test) 3 print(pd.crosstab(kn_pred,y_test)) 4 5 # 模型得分 6 print("模型在训练集上的准确率%f"%kn.score(X_train,y_train)) 7 print("模型在测试集上的准确率%f"%kn.score(X_test,y_test))
结果如下
income 0 1
row_0
0 5637 723
1 589 1192
模型在训练集上的准确率0.890500
模型在测试集上的准确率0.838840
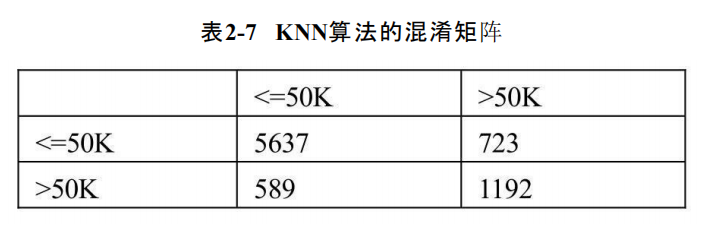
如上结果所示,第一部分(计算结果)是混淆矩阵,矩阵中的行是模型的预测值,矩阵中的列是测试集的实际值,主对角线就是模型预测正确的数量(5637和1192),589和723就是模型预测错误的数量。经过计算,得到第二部分(表2-7)的结论,即模型在训练集中的准确率为89.1%,但在测试集上的错误率超过16%(1-0.839),说明默认参数下的KNN模型可能存在过拟合的风险。模型的准确率就是基于混淆矩阵计算的,但是该方法存在一定的弊端,即如果数据本身存在一定的不平衡时(正负样本的比例差异较大),一定会导致准确率很高,但并不一定说明模型就是理想的。这里再介绍一种常用的方法,就是绘制ROC曲线,并计算曲线下的面积AUC值:
1 # 导入模型评估模块 2 from sklearn import metrics 3 4 # 计算ROC曲线的X轴和Y轴 5 fpr,tpr,_ = metrics.roc_curve(y_test,kn.predict_proba(X_test)[:,1]) 6 7 # 绘制ROC曲线 8 plt.plot(fpr,tpr,linestyle="solid",color="red") 9 10 # 添加阴影 11 plt.stackplot(fpr,tpr,color="steelblue") 12 13 # 绘制参考线 14 plt.plot([0,1],[0,1],linestyle="dashed",color="black") 15 16 # 往图中添加文本 17 plt.text(0.6,0.4,"AUC=%.3f"%metrics.auc(fpr,tpr),fontdict=dict(size=18)) 18 plt.show()
结果如下KNN算法的ROC曲线图:
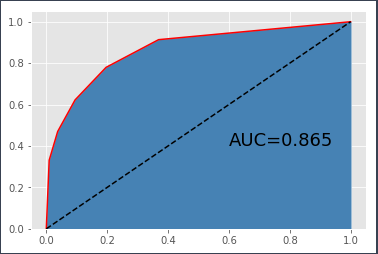
图中绘制了模型的ROC曲线,经计算得知,该曲线下的面积AUC为0.865。如果使用AUC来评估模型的好坏,那应该希望AUC越大越好。一般而言,当AUC的值超过0.8时,基本上就可以认为模型比较合理。所以,基于默认参数的K近邻模型在居民收入数据集上的表现还算理想。
7、网格搜索K近邻模型
1 # 预测数据集 2 grid_kn_pred = grid_kn.predict(X_test) 3 print(pd.crosstab(grid_kn_pred,y_test)) 4 5 # 模型得分 6 print("模型在训练集上的准确率%f"%grid_kn.score(X_train,y_train)) 7 print("模型在测试集上的准确率%f"%grid_kn.score(X_test,y_test)) 8 9 # 绘制ROC曲线 10 fpr ,tpr ,_ = metrics.roc_curve(y_test,grid_kn.predict_proba(X_test)[:,1]) 11 plt.plot(fpr,tpr,linestyle="solid",color="red") 12 plt.stackplot(fpr,tpr,color="steelblue") 13 plt.plot([0,1],[0,1],linestyle="dashed",color="black") 14 plt.text(0.6,0.4,"AUC=%.3f"%metrics.auc(fpr,tpr),fontdict=dict(size=18)) 15 plt.show()
结果如下:
income 0 1 row_0 0 5834 867 1 392 1048 模型在训练集上的准确率0.882473 模型在测试集上的准确率0.845351

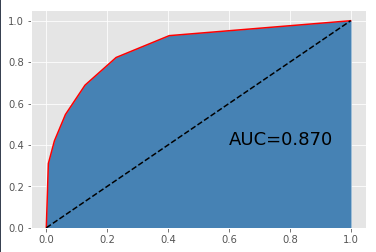
相比于默认参数的K近邻模型来说,经过网格搜索后的模型在训练数据集上的准确率下降了,但在测试数据集上的准确率提高了,这也是我们所期望的,说明优化后的模型在预测效果上更加优秀,并且两者差异的缩小也能够降低模型过拟合的可能。再来看看ROC曲线下的面积,网格搜索后的K近邻模型所对应的AUC为0.87,相比于原先的KNN模型提高了一点。所以,从模型的稳定性来看,网格搜索后的K近邻模型比原始的K近邻模型更加优秀。
8、默认的GBDT模型
1 # 预测测试集 2 gbdt_pred = gbdt.predict(X_test) 3 print(pd.crosstab(gbdt_pred,y_test)) 4 5 # 模型得分 6 print("模型在训练集上的准确率%f"%gbdt.score(X_train,y_train)) 7 print("模型在测试集上的准确率%f"%gbdt.score(X_test,y_test)) 8 9 # 绘制ROC曲线 10 fpr ,tpr ,_ = metrics.roc_curve(y_test,gbdt.predict_proba(X_test)[:,1]) 11 plt.plot(fpr,tpr,linestyle="solid",color="red") 12 plt.stackplot(fpr,tpr,color="steelblue") 13 plt.plot([0,1],[0,1],linestyle="dashed",color="black") 14 plt.text(0.6,0.4,"AUC=%.3f"%metrics.auc(fpr,tpr),fontdict=dict(size=18)) 15 plt.show()
结果如下:
income 0 1 row_0 0 5862 784 1 364 1131 模型在训练集上的准确率0.869451 模型在测试集上的准确率0.858985
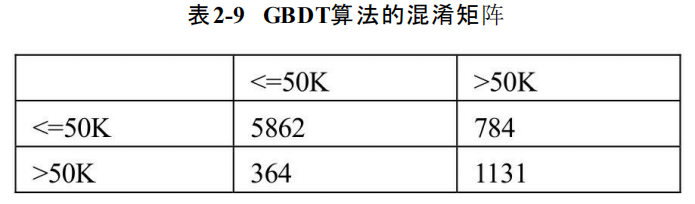
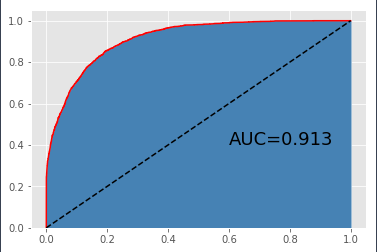
如上结果所示,集成算法GBDT在测试集上的表现明显要比K近邻算法优秀,这就是基于多棵决策树进行投票的优点。该模型在训练集和测试集上的表现都非常好,准确率均超过85%,而且AUC值也是前面两种模型中最高的,达到了0.913。
9.网络搜索的GBDT模型
1 # 预测测试集 2 grid_gbdt_pred = grid_gbdt.predict(X_test) 3 print(pd.crosstab(grid_gbdt_pred,y_test)) 4 5 # 模型得分 6 print("模型在训练集上的准确率%f"%grid_gbdt.score(X_train,y_train)) 7 print("模型在测试集上的准确率%f"%grid_gbdt.score(X_test,y_test)) 8 9 # 绘制ROC曲线 10 fpr ,tpr ,_ = metrics.roc_curve(y_test,grid_gbdt.predict_proba(X_test)[:,1]) 11 plt.plot(fpr,tpr,linestyle="solid",color="red") 12 plt.stackplot(fpr,tpr,color="steelblue") 13 plt.plot([0,1],[0,1],linestyle="dashed",color="black") 14 plt.text(0.6,0.4,"AUC=%.3f"%metrics.auc(fpr,tpr),fontdict=dict(size=18)) 15 plt.show()
结果如下:
income 0 1 row_0 0 5842 667 1 384 1248 模型在训练集上的准确率0.890336 模型在测试集上的准确率0.870900
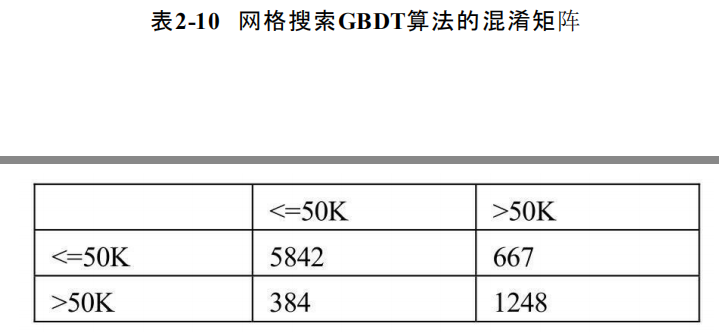
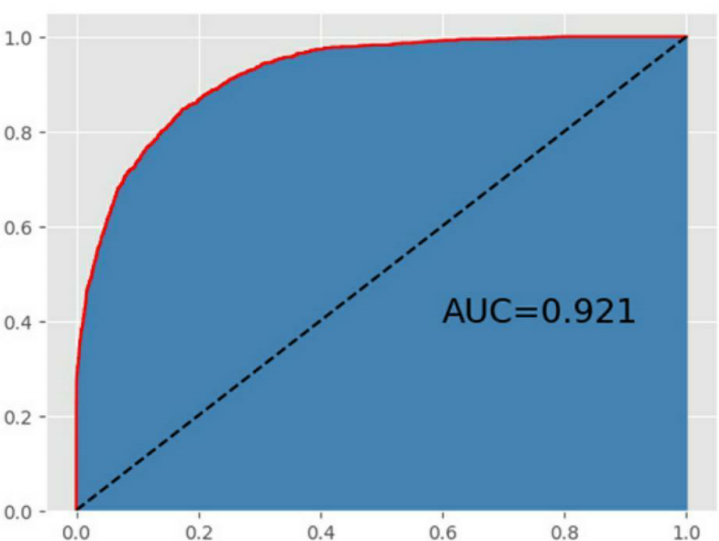
如上展示的是基于网格搜索后的GBDT模型的表现,从准确率来看,是4个模型中表现最佳的,该模型在训练集上的准确率接近90%,同时,在测试集上的准确率也超过87%;从绘制的ROC曲线来看,AUC的值也是最高的,超过0.92。
不论是K近邻模型,还是梯度提升树GBDT模型,都可以通过网格搜索法找到各自的模型参数,而且这些最佳参数的组合一般都会使模型比较优秀和健壮。所以,纵向比较数的模型和网格搜索后的最佳参数模型,后者可能是比较好的选择(尽管后者可能会花的运行时间);横向比较单一模型和集成模型,集成模型一般会比单一模型表现优
