朴素贝叶斯(Naive Bayes)是一个非常简单,但是实用性很强的分类模型。朴素贝叶斯分类器的构造基础是贝叶斯理论。
概率论基础
概率定义为一件事情发生的可能性。事情发生的概率可以 通过观测数据中的事件发生次数来计算,事件发生的概率等于该事件发生次数除以所有事件发生的总次数。举一些例子:
- 扔出一个硬币,结果头像朝上
- 某天是晴天
- 某个单词在未知文档中出现
我们将事件的概率记作P(X),那么假设这一事件X属于样本空间中的一个类别,那么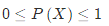
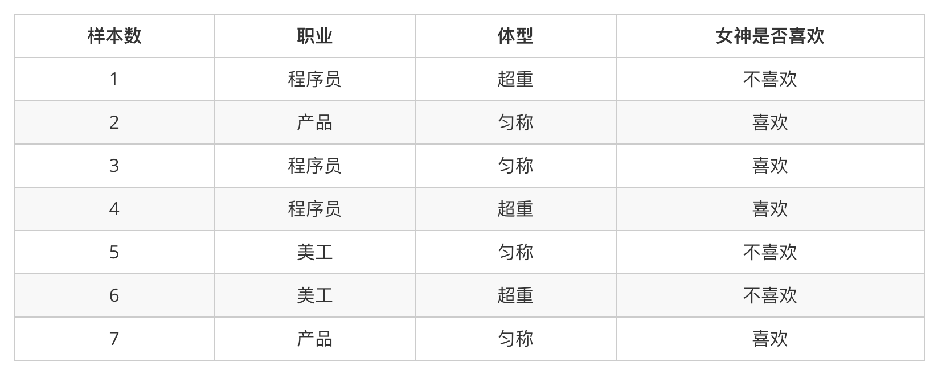
问题:
- 女神喜欢的概率?
答案:4/7 - 职业是程序员并且体型匀称的概率?
答案:P(程序员, 匀称)=(3/7) * (4/7) = 12/49 - 在女神喜欢的条件下,职业是程序员的概率?
答案:2/4 = 1/2 - 在女神喜欢的条件下,职业是产品,体重是超重的概率?
答案:P(产品, 超重|喜欢) = P(产品|喜欢) P(超重|喜欢) = (1/2) * (1/4) = 1/8
联合概率和条件概率
联合概率:包含多个条件,且所有条件同时成立的概率。记作:P(A,B)
条件概率:就是事件A在另外一个事件B已经发生的条件下发生的概率。记作P(A | B)
特性:P(A1, A2|B) = P(A1,B)P(A2|B)
注意:此条件概率的成立,是由于A1,A2相互独立的结果
朴素贝叶斯-贝叶斯公式
首先我们给出该公式的表示:
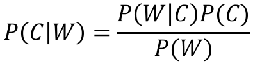
注:W为给定文档的特征值(频数统计,预测文档提供),C为文档类别
贝叶斯公式最常用于文本分类,上式左边可以理解为:
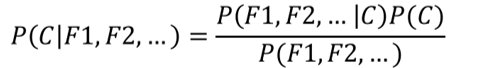
其中C可以是不同类别
公式分为三个部分:



训练集统计结果(指定统计词频):
| 特征统计 | 科技(30篇) | 娱乐(60篇) | 汇总(90篇) |
|---|---|---|---|
| 商场 | 9 | 51 | 60 |
| 影院 | 8 | 56 | 64 |
| 支付宝 | 20 | 15 | 35 |
| 云计算 | 63 | 0 | 63 |
| 汇总(求和) | 100 | 121 | 221 |
现有一篇被预测文档:出现了影院,支付宝,云计算,计算属于科技、娱乐的类别概率?
科技:P(科技|影院,支付宝,云计算) = P(影院,支付宝,云计算|科技) * P(科技) = (8/100) * (20/100) * (63/100) * (30/90) = 0.00336
娱乐:P(娱乐|影院,支付宝,云计算) = P(影院,支付宝,云计算|娱乐) * P(娱乐) = (56/121) * (15/121) * (0/121) * (60/90) = 0
上面计算的属于娱乐的概率为0是否不合理?
拉普拉斯平滑
上面的例子我们得出娱乐的概率为0,这是不合理的,如果词频列表里面有很多出现次数为0,很可能计算结果都为0。
解决方法:拉普拉斯平滑系数
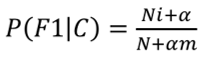
α指定的系数一般为1,m为训练文本中统计出的特征词的个数。
重新计算如下:
科技:P(科技|影院,支付宝,云计算) = P(影院,支付宝,云计算|科技) * P(科技) = (8+1)/(100+(14)) * ((20+1)/(100+(14))) * ((63+1)/(100+(1*4))) * (30/90) = 0.0035844333181611282
娱乐:P(娱乐|影院,支付宝,云计算) = P(影院,支付宝,云计算|娱乐) * P(娱乐) = (56+1)/(121+14) * (15+1)/(121+14) * (0+1)/(121+1*4) * (60/90) = 0.00031129599999999997
sklearn朴素贝叶斯API
sklearn.naive_bayes.MultinomialNB(alpha = 1.0):朴素贝叶斯分类
alpha:拉普拉斯平滑系数
案例:sklearn20类新闻分类
from sklearn.datasets import fetch_20newsgroups
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import MultinomialNB
from sklearn.feature_extraction.text import TfidfVectorizer
# 加载新闻数据
news = fetch_20newsgroups()
# 进行切割
x_train, x_test, y_train, y_test = train_test_split(news.data,
news.target, test_size=0.25)
# 特征提取
tfidf = TfidfVectorizer()
x_train = tfidf.fit_transform(x_train)
x_test = tfidf.transform(x_test)
# print(tfidf.get_feature_names)
mlt = MultinomialNB(alpha=1.0)
mlt.fit(x_train, y_train)
y_predict = mlt.predict(x_test)
print("预测的文章类别为:", y_predict)
print("准确率为:", mlt.score(x_test, y_test))
运行结果:
预测的文章类别为: [ 2 9 12 ... 9 12 12]
准确率为: 0.8370448921880523
朴素贝叶斯分类优缺点
优点:
- 朴素贝叶斯模型发源于古典数学理论,有稳定的分类效率。
- 对缺失数据不太敏感,算法也比较简单,常用于文本分类。
- 分类准确度高,速度快
缺点:
- 需要知道先验概率P(F1,F2,…|C),因此在某些时候会由于假设的先验模型的原因导致预测效果不佳。