割平面法
割平面法由Gomory'于1958年提出的一种求解整数规划问题的方法,计算步骤如下:
一、用单纯形法求解(IP)对应的松弛问题(LP)
- 若(LP)没有可行解,则(IP)也没有可行解,停止计算。(若松弛问题没有可行解,则原整数问题也没有可行解,停止计算)
- 若(LP)有最优解,并符合(IP)的整数条件,则(LP)的最优解即为(IP)的最优解,停止计算。(若松弛问题有最优解,并符合原整数问题的整数条件,则该最优解即为原整数问题的最优解,停止计算)
- 若(LP)有最优解,但不符合(IP)的整数条件,转入下一步。
二、从(LP)的最优解中,任选一个不为整数的分量xr,将最优单纯形表中该行的系数a‘rj和br分解为整数部分和小数部分之和,并以该行为源行,按下式作割平面方程:

三、将所得的割平面方程作为一个新的约束条件置于最优单纯形表中(同时增加一个单位列向量),用对偶单纯形法求出新的最优解,返回一.
例子
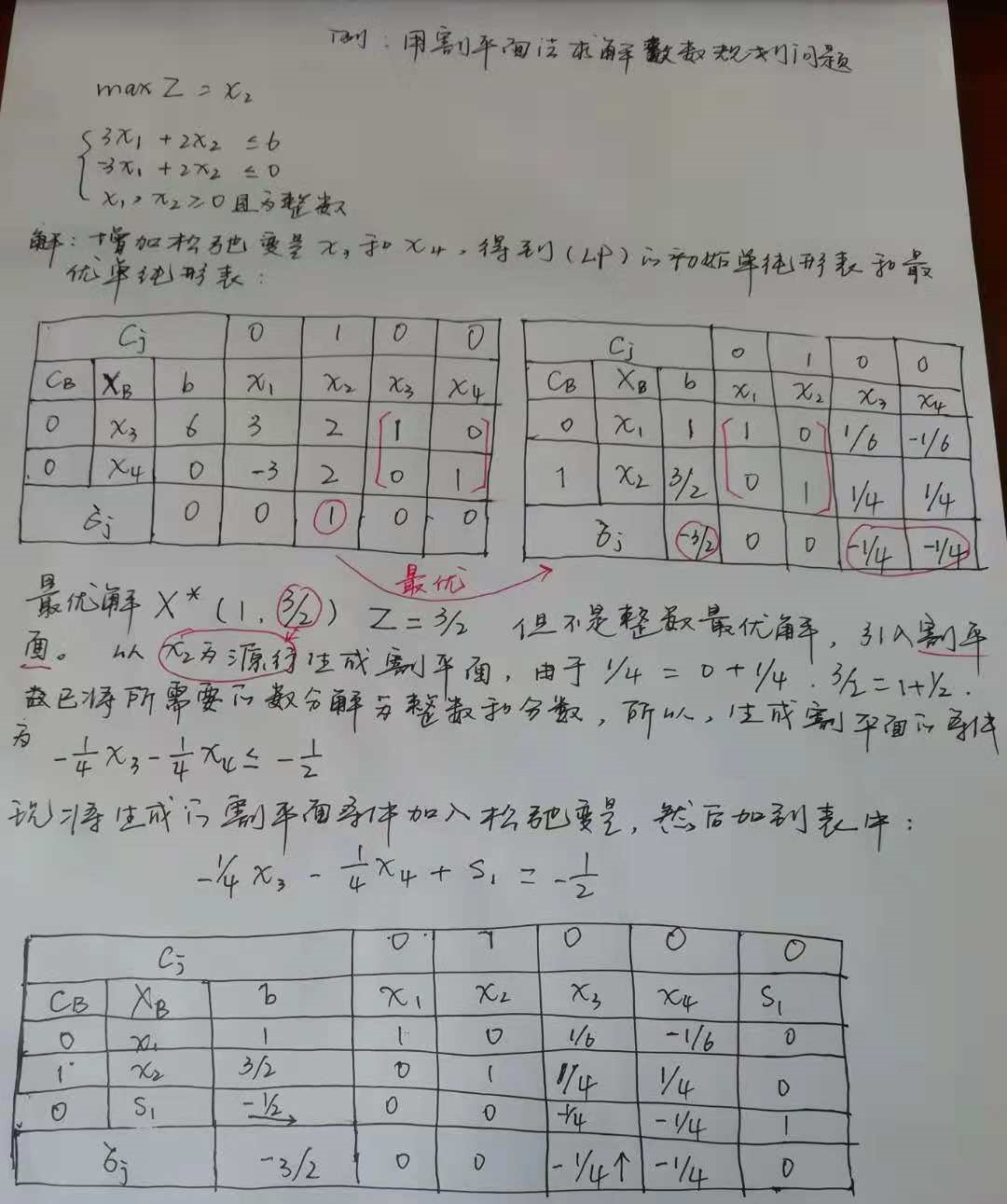
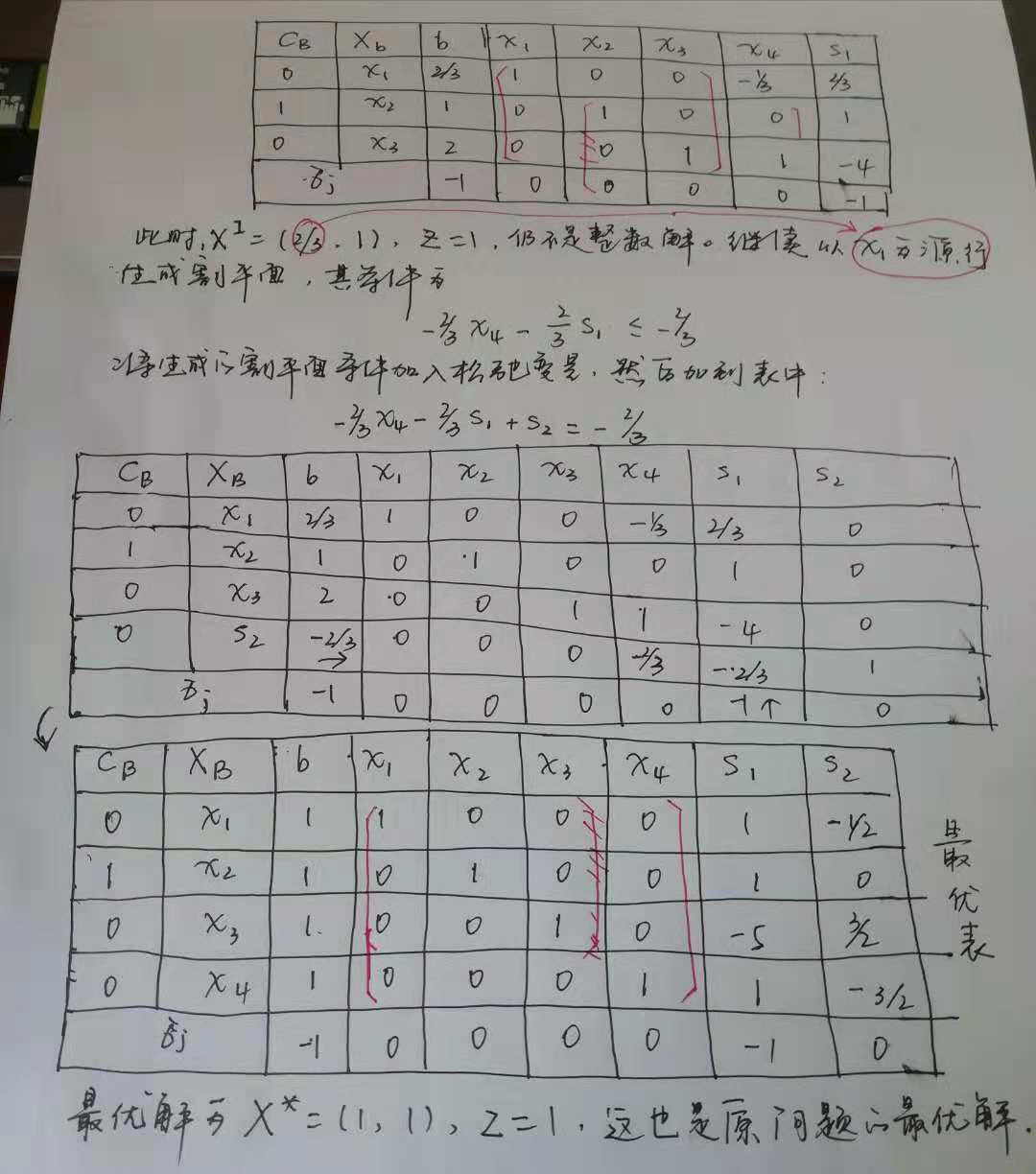
由以上解题过程可见,表中含有分数元素且算法过程中始终保持对偶可行性,因此,这个算法也称为分数对偶割平面算法。