题意
给你一个有 (n) 个点的图 里面有 (m) 条边
并给你图上一条哈密顿回路 然后让你判断它是否为平面图
平面图就是存在一种情况 使得边两两不相交 数据共 (T) 组
[(T le 100 , 3 le n le 200, m le 10000)
]
题解
这题是我见过最不裸的 (2-SAT) 了 根本不会啊
判断平面图 有一些鬼畜的算法可以做 但根本不会啊
这题比较特殊 给了一条哈密顿回路 那么我们可以利用这个性质
不难发现 如果两条边会相交 那么他们不能同时存在 在 哈密顿圈 内 或者 外面
这样 我们对于原图中每条边就变成 (2-SAT) 上的点然后去判断就行了
至于判边相交 考虑如下一种情况
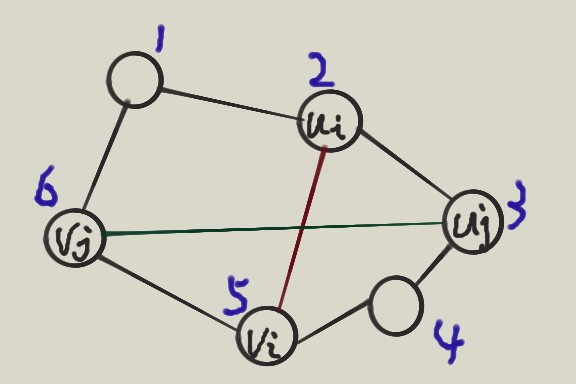
我们将这个环重新标号 标为 (1 o 6)
然后如果两条边 (设为 (u_i o v_i) 和 (u_j o v_j) 强制 (u_i < u_j , u_i < v_i , u_j < v_j) ) 会相交 那么我们就有一个不等式
[u_i < u_j < v_i < v_j
]
所有相交情况都可以这样转化
但数据组数多 边的范围原超过点的范围 可能会TLE
所以我们就可以用个性质进行一些优化
平面图上 边数 (E) 和 点数 (V) 满足 (E le V * 3 - 6)
这个一开始直接判就行了qwq
代码
有一些鬼畜的地方 就是点和边的范围 以及 他们一开始清空的范围
/**************************************************************
Problem: 1997
User: zjp_shadow
Language: C++
Result: Accepted
Time:180 ms
Memory:10440 kb
****************************************************************/
#include <bits/stdc++.h>
#define For(i, l, r) for(register int i = (l), i##end = (int)(r); i <= i##end; ++i)
#define Fordown(i, r, l) for(register int i = (r), i##end = (int)(l); i >= i##end; --i)
#define Set(a, v) memset(a, v, sizeof(a))
using namespace std;
inline bool chkmin(int &a, int b) {return b < a ? a = b, 1 : 0;}
inline bool chkmax(int &a, int b) {return b > a ? a = b, 1 : 0;}
inline int read() {
int x = 0, fh = 1; char ch = getchar();
for (; !isdigit(ch); ch = getchar()) if (ch == '-') fh = -1;
for (; isdigit(ch); ch = getchar()) x = (x * 10) + (ch ^ 48);
return x * fh;
}
void File() {
#ifdef zjp_shadow
freopen ("1997.in", "r", stdin);
freopen ("1997.out", "w", stdout);
#endif
}
const int N = 110000 << 1, M = 100100 << 1;
struct Two_SAT {
#define Travel(i, u, v) for(int i = Head[u], v = to[i]; i; i = Next[i], v = to[i])
int Head[N], Next[M], to[M], e, n;
void add_edge(int u, int v) { to[++ e] = v; Next[e] = Head[u]; Head[u] = e; }
void Add(int x, int xv, int y, int yv) {
x = x << 1 | xv;
y = y << 1 | yv;
add_edge(x, y);
add_edge(y ^ 1, x ^ 1);
}
void Init(int n) {
this -> n = n; e = 0;
For (i, 1, n * 2 + 10) Head[i] = 0;
}
int sccno[N], scc_cnt;
int clk, dfn[N], lowlink[N];
int sta[N], top;
void Tarjan(int u) {
lowlink[u] = dfn[u] = ++ clk; sta[++ top] = u;
Travel(i, u, v)
if (!dfn[v]) Tarjan(v), chkmin(lowlink[u], lowlink[v]);
else if (!sccno[v]) chkmin(lowlink[u], dfn[v]);
if (lowlink[u] == dfn[u]) {
++ scc_cnt;
for (;;) {
int x = sta[top --];
sccno[x] = scc_cnt;
if (x == u) break;
}
}
}
bool Solve() {
For (i, 1, n * 2 + 10)
dfn[i] = sccno[i] = lowlink[i] = 0;
scc_cnt = clk = top = 0;
For (i, 1, n * 2 + 1)
if (!dfn[i]) Tarjan(i);
For (i, 1, n)
if (sccno[i << 1] == sccno[i << 1 | 1]) return false;
return true;
}
} T;
struct Edge{
int u, v;
inline bool operator < (const Edge &rhs) const {
return (u ^ rhs.u) ? u < rhs.u : v < rhs.v;
}
} lt[M];
int ver[N], num[N];
int main () {
File();
int cases = read();
while (cases --) {
int n = read(), m = read();
For (i, 1, m) {
lt[i].u = read();
lt[i].v = read();
}
For (i, 1, n) {
ver[i] = read();
num[ver[i]] = i;
}
if (m > 3 * n - 6) { puts("NO"); continue; }
For (i, 1, m) {
lt[i].u = num[lt[i].u];
lt[i].v = num[lt[i].v];
if (lt[i].u > lt[i].v) swap(lt[i].u, lt[i].v);
}
sort(lt + 1, lt + 1 + m);
T.Init(n);
For (i, 1, m) For (j, i + 1, m) {
if (lt[i].u == lt[i].v - 1 || (lt[i].u == 1 && lt[i].v == n)) continue ;
if (lt[i].u < lt[j].u && lt[j].u < lt[i].v && lt[i].v < lt[j].v) {
T.Add(i, 1, j, 0);
T.Add(i, 0, j, 1);
}
}
puts(T.Solve() ? "YES" : "NO");
}
return 0;
}