1.查找的相关概念
查找:在n个记录里,寻找关键字等于目标k的过程,唯一匹配数据数据元素的数据项称为主关键字,其余数据项称为次关键字。
平均查找长度:反映统计意义上的多次查找的平均查找长度。
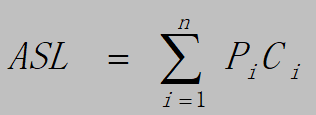
查找的方法:线性查找
2.线性查找(顺序查找)
从记录起始开始,逐个匹配记录信息,直到寻到目标关键字,若到最后仍未有相关信息,进行提示输出。
//顺序查找
int SeqSearch(int r[],int n,int k)
{
r[n].key=k; //目标信息
i=0;
while (r[i].key!=k) //关键字匹配
i++;
return(i);
}
说明:若返回n表明查找不成功。
链式存储结构:
{
p=h->next;
while ((p!=NULL) && (p->key!=k)) p=p->next;
return p;
}
性能分析:
3.对分查找(拆半查找)
针对有序表的一种查找方式,先比较中间记录关键字信息,若匹配则输出,大于中间记录,则查找后半区间,若小于中间记录,则查找上半区间,由此递归查询,直到获得匹配信息。
对分查找
int BinSearch(int r[],int n,int k)
{
int low=0,hig=n-1;
while (low<=hig){
mid=(low+hig)/2; //中间记录
if (k==r[mid]) return(1);
if (k<r[mid]) hig=mid-1;
if (k>r[mid]) low=mid+1;
}
return(0);
}
性能分析:ASL = log2(n+1) + 1
优点是平均查找长度小,但是需要是顺序表,适用于建立后不需要多加改变同时需要大量查找操作的顺序表。
4.分块查找(索引顺序查找)
把所有关键字分块,并且后面的关键字的值均大于前一块,快内的关键字保持无序。查找过程是先使用顺序查找或对分查找确定关键字块,再在块内进行顺序查找。性能介于顺序查找和对分查找之间。
5.二叉排序树查找
将待查信息与根节点关键字进行比较,匹配则输出,小于则进入左子树,大于则进入右子树,依次循环查找。
int BstSearch(NODE *t,int k)
{
if (t){
if (k==p->data) return(1); //根节点
if (k<p->data) BstSearch(t->lchild,k);//查找左子树
if (k>p->data) BstSearch(t->rchild,k);//查找右子树
}
else return(0);
}
性能分析:与二叉排序树结构相关,最好情况下,为均匀的二叉树,平均查找长度与二分查找相近,为log2n,最坏情况为单子树,平均查找长度为(n+1)/2。
6.哈希查找
通过对给定值进行一定运算,直接求得与指定值信息匹配的关键字的位置。
哈希函数、哈希地址、哈希表、装填系数(a=n/m,一般为0.65-0.85)、非数值关键字的内部码、冲突(不同关键字的系统哈希地址)、同义词
6.1哈希查找的几种技术
6.1.1数字分析法
适合静态数据,关键字已知,分析数字的分布,删除不均匀的数字,再根据存储空间决定数字的数目。
6.1.2平方取中法
关键字平方,选取其中几位作为哈希地址
6.1.3除留余数法
对关键字取模(余数)作为哈希地址
6.1.4折叠法
将关键字拆分成几段,除了最后一段每段长度均相等,再将各段相加作为哈希地址。包括移位折叠(字段左靠齐后相加)和边界折叠(偶数字段倒排,最后字段右考)两种。
6.2解决冲突的方法
6.2.1线性探测再散列
线性表空间为T[m],哈希函数为H,冲突时另一个记录的地址公式为 dj+1=(d1+j) % m (j=1,2,…,s,s≥1),其中d1=H(key)。即在冲突时,以线性的方式从下一个哈希地址开始探测,直到查到下一个空的存储地址。若一个循环还没有找到空间,说明地址已满。
LineSearch(T,k,m)
{
i=H(k); j=i;
while (T[j].key!=k && T[j].key!=0){
j=(j+1)%m;
if (j==i){ 表满;return(-1);}
}
return(j);
}
缺点:易造成关键字聚集,增加查找时间。
6.2.2平方探测再散列
改善线性探测的缺点,避免关键字的聚集。

6.2.3随机探测再散列
用一组预先给定的随机数求冲突时的地址,公式为: dj=(d1+Rj) % m (j=1,2,...,s,s≥1) 其中Rj为一组随机数列。
6.2.4链地址法
在哈希表中设置一个由m个指针分量组成的一位数组,凡哈希地址为i的记录都插入到头指针为ST[i]的链表中,适用于造表前无法确定记录个数的情况。
ChnSearch(ST,m,k)
{
i=H(k); p=ST[i];
while (p && p->data!=k) p=p->next;
return(p);
}