Description
A tree is a well-known data structure that is either empty (, void, nothing) or is a set of one or more nodes connected by directed edges between nodes satisfying the following properties. There is exactly one node, called the root, to which no directed edges point.
Every node except the root has exactly one edge pointing to it.
There is a unique sequence of directed edges from the root to each node.
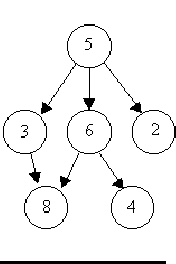
For example, consider the illustrations below, in which nodes are represented by circles and edges are represented by lines with arrowheads. The first two of these are trees, but the last is not.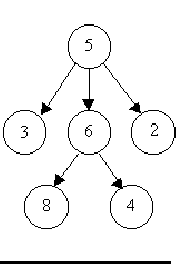
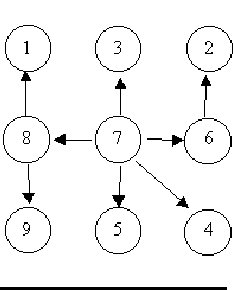
Every node except the root has exactly one edge pointing to it.
There is a unique sequence of directed edges from the root to each node.
For example, consider the illustrations below, in which nodes are represented by circles and edges are represented by lines with arrowheads. The first two of these are trees, but the last is not.



Input
The input will consist of a sequence of descriptions (test cases) followed by a pair of negative integers. Each test case will consist of a sequence of edge descriptions followed by a pair of zeroes Each edge description will consist of a pair of integers; the first integer identifies the node from which the edge begins, and the second integer identifies the node to which the edge is directed. Node numbers will always be greater than zero.
Output
For each test case display the line ``Case k is a tree." or the line ``Case k is not a tree.", where k corresponds to the test case number (they are sequentially numbered starting with 1).
Sample Input
6 8 5 3 5 2 6 4 5 6 0 0 8 1 7 3 6 2 8 9 7 5 7 4 7 8 7 6 0 0 3 8 6 8 6 4 5 3 5 6 5 2 0 0 -1 -1
Sample Output
Case 1 is a tree. Case 2 is a tree. Case 3 is not a tree.
 View Code
View Code
1 #include <stdio.h>
2 int set[105];
3 int a, b, a1, b1;
4 void make_set()
5 {
6 for(int i = 0; i < 105; i++)
7 set[i] = -i;
8 }
9 int find(int x)
10 {
11 if(set[x] == x)
12 return x;
13 if(set[x] == -x)
14 return -x;
15 else
16 set[x] = find(set[x]);
17 return set[x];
18 }
19 int main()
20 {
21 int q = 1, num = 0;
22 int judge = 0,flag = 0;
23 make_set();
24 while( scanf("%d%d",&a,&b) == 2 && a >= 0 )
25 {
26
27 if(a != 0)
28 {
29 flag = 1;
30 a1 = find(a);
31 if(a1 == -a)
32 set[a] = a;
33 b1 = find(b);
34 if(b1 == -b)
35 set[b] = b;
36 if(a1 == b1)
37 {
38 num = 0;
39 judge = 1;
40 }
41 if(judge == 0)
42 {
43 if(b1 == b)
44 {
45 if(a1 != -a)
46 {
47 num--;
48 }
49 set[b] = find(a);
50 }
51 else
52 {
53 if(b1 == -b)
54 {
55 if(a1 == -a)
56 {
57
58 num++;
59 }
60 set[b] = find(a);
61 }
62 else
63 {
64 num = 0;
65 judge = 1;
66 }
67 }
68 }
69 }
70 else
71 {
72 if( num == 1 || flag == 0 )
73 printf("Case %d is a tree.\n",q);
74 else
75 printf("Case %d is not a tree.\n",q);
76 q++;
77 flag = 0;
78 num = 0;
79 judge = 0;
80 make_set();
81 }
82 }
83 return 0;
84 }
85
