题目描述
如题,给出一个N次函数,保证在范围[l,r]内存在一点x,使得[l,x]上单调增,[x,r]上单调减。试求出x的值。
输入输出格式
输入格式:
第一行一次包含一个正整数N和两个实数l、r,含义如题目描述所示。
第二行包含N+1个实数,从高到低依次表示该N次函数各项的系数。
输出格式:
输出为一行,包含一个实数,即为x的值。四舍五入保留5位小数。
说明
时空限制:50ms,128M
数据规模:
对于100%的数据:7<=N<=13
思路:
这是一道三分的模板题,在这里我讲一下三分
三分是什么??:
三分是一种优化的暴力,从他的名字就可以知道,这是一种很类似于二分的方法,通过一系列操作时复杂度由O(n)降到O(logn)
三分能干什么?
求单峰多次函数最值位置(近似值)
如何实现三分?(这个是重点)
我们先看一幅图(picture by luogu)
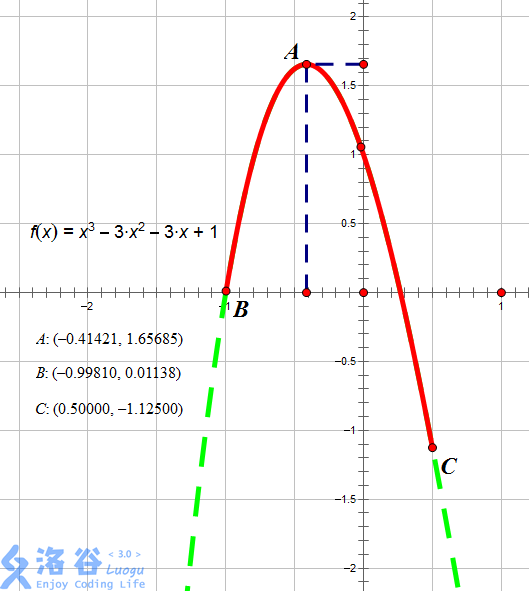
现在我们的已知条件有峰所在的区间和函数表达式,这就很好办
首先我们取区间中点
然后取离中点很近的两个点(距离必须小于等于要求精度),并求出它们的函数值
这时候通过判断函数值的大小就可以知道此处是递增还是递减
如果递增,那点就在左区间,峰在其右,区间左端点就变成区间中点
反之亦然
一直缩小区间大小
到满足精度时,答案就呼之欲出
一点小优化:
高中的同学应该都知道有个东西叫秦九韶算法
它可以将a0+a1*x^1+a2*x^2……an^xn这个高复杂度的东西
优化为an(x+an-1(x……a1(x+a0)))这个线性的式子
复杂度下降了一个log
很好使
见代码:
#include<iostream>
#include<cstdio>
#include<cmath>
#define rii register int i
using namespace std;
int n;
double xs[15],l,r,final,mid;
double eps=0.000001;
double dxs(double z)
{
double ans=0;
for(rii=n;i>=0;i--)
{
ans=ans*z+xs[i];
}
return ans;
}
int main()
{
cin>>n>>l>>r;
for(rii=n;i>=0;i--)
{
cin>>xs[i];
}
eps=0.000001;
while(1)
{
if(fabs(r-l)<eps)
{
final=r;
break;
}
mid=(l+r)/2;
if(dxs(mid+eps)>dxs(mid-eps))
{
l=mid;
}
else
{
r=mid;
}
}
printf("%.5lf",final);
}