1005 :
Fibonacci Sum
从斐波那契的通项入手。
思路:

所以 $ans = \sum_{i = 0}^{n} ans1^k = \sum_{i = 0}^{n} \frac{1}{T^k} (b^i-c^i)^k$
令$f[i] = (b^i-c^i)^k$
那么ans = $\frac{1}{T^k} * \sum_{i = 0}^{n} f[i]$
首先对f[i]二项式展开,然后求和合并之后。
可以发现$sum = C(k,0) *(-1)^k( (a^0)^0*(b^0)^k+(a^1)^0*(b^1)^k +....)+C(k,1)... $
对于C(k,i)里的每一项是一个等比数列的求和。
那么可以O(1)求出。最后枚举k去算总和即可
由于这里常数过大,所以先预处理一下逆元。
同时由于n稍微大了些。
所以通过欧拉降幂公式,因为模数为质数。
a^b % p = a^(b % (p-1)) % p
然后因为C(k,i)之间公比是乘a/b倍的,所以不需要每次都快速幂求公比。
只需要前面的公比*a/b即可。
还有当公比为1时中间等比数列求和的分母为0,这时不用求和公式,直接可以发现其中每项都是1,那么求和就是n
Code:

#include<bits/stdc++.h> using namespace std; typedef long long LL; typedef long double ld; typedef pair<int,int> pii; const int N = 1e5+5; const LL Mod = 1e9+9; #define pi acos(-1) #define INF 1e8 #define INM INT_MIN #define dbg(ax) cout << "now this num is " << ax << endl; LL a = 691504013,b = 308495997,d = 383008016; LL f[N],inv[N]; inline LL read() { LL x = 0,f = 1;char c = getchar(); while(c < '0' || c > '9'){if(c == '-') f = -1;c = getchar();} while(c >= '0' && c <= '9'){x = (x<<1)+(x<<3)+(c^48);c = getchar();} return x*f; } LL quick_mi(LL a,LL b) { LL re = 1; a %= Mod; while(b) { if(b&1) re = (re*a)%Mod; a = (a*a)%Mod; b >>= 1; } return re; } void init() { f[0] = 1; for(int i = 2;i < N;++i) f[i] = f[i-1]*i%Mod; inv[N-1] = quick_mi(f[N-1],Mod-2); for(int i = N-2;i >= 0;--i) inv[i] = inv[i+1]*(i+1)%Mod; } LL C(LL n,LL m) { return f[n]*inv[m]%Mod*inv[n-m]%Mod; } LL slove(LL n,LL c,LL k) { LL A = quick_mi(a,c%(Mod-1)),B = quick_mi(b,c%(Mod-1)); LL aa = 1,bb = quick_mi(B,k),tmp = quick_mi(B,Mod-2);//预处理第一项公比 LL ans = 0; for(LL i = 0;i <= k;++i) { LL x = aa*bb%Mod;//求出公比 LL ma = C(k,i); LL sum = x*(quick_mi(x,n%(Mod-1))-1+Mod)%Mod*quick_mi(x-1,Mod-2)%Mod;//等比数列求和 if(x == 1) sum = n%Mod;//公比为1时 if((k-i) & 1) ans = (ans-ma*sum%Mod)%Mod;//-1是偶次还是幂次 else ans = (ans+ma*sum%Mod)%Mod; aa = aa*A%Mod*tmp%Mod;//公比递推 } LL ta = quick_mi(d,Mod-2); ans = ans*quick_mi(ta,k)%Mod; ans = (ans%Mod+Mod)%Mod; return ans; } int main() { init(); int t;t = read(); while(t--) { LL n,c,k; n = read(),c = read(),k = read(); LL ans = slove(n,c,k); printf("%lld\n",ans); } // system("pause"); return 0; }
1009:
Leading Robots
思路:
有非常多的解法。
1:
我们知道x = x0+1/2 a*t*2.
那么以t^2为横坐标,x为纵坐标来建xoy坐标系。
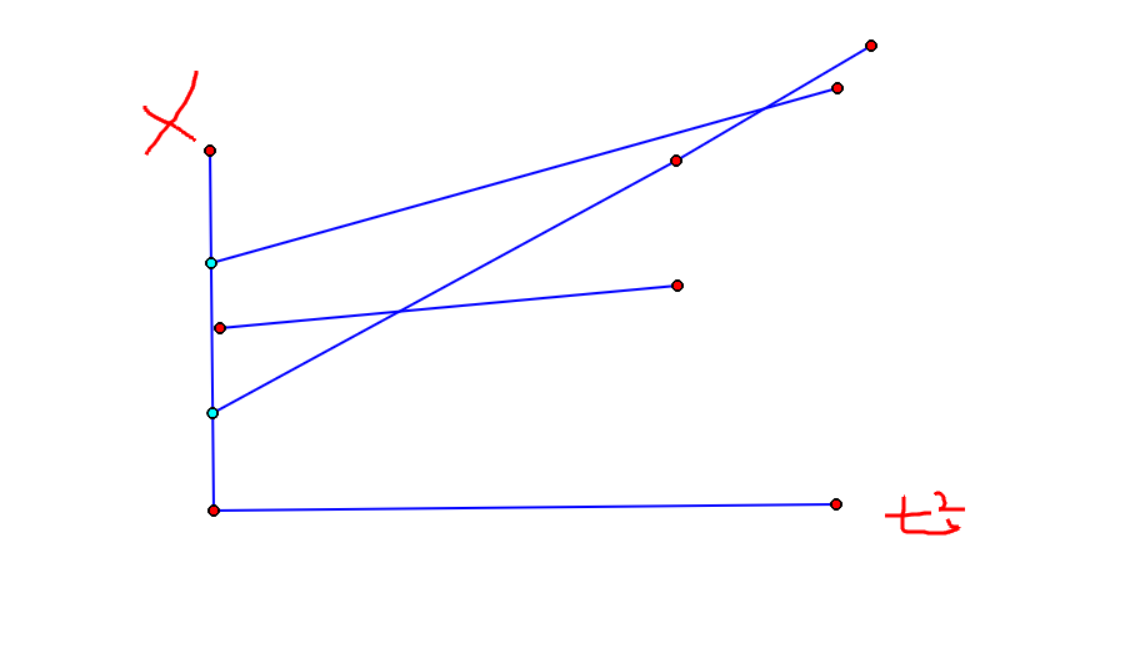
那么先按x坐标来排序,之后我们从下往上扫,来判断每条直线是否可以成为领队,同时用一个单调栈来维护领队
当当前直线的a >= 栈顶直线的a时,显然在他右边的而且a还大于它,那么栈顶元素不可能成为领队,所以栈顶出栈。
否则判断当前直线与栈顶相遇 的时间是否 <= 栈顶元素和栈内栈下一个元素的相遇时间。如果是,那么显然在栈顶元素成为领队前就会被当前直线超到。那么栈顶出栈。
注意的是时间是t^2,然后用mp来维护一下重复的点,有重合那么该点不可能为领队。
2.形象理解。
将所有元素按加速度升序。同样单调栈来维护领队。
对于当前,那么显然之后的元素a 都 >= 栈顶。
如果这时当前元素的 x >= 栈顶元素。同样的栈顶出栈
那么只需要判断 当前元素遇到栈顶的时间是否 <= 栈顶 与栈内栈顶下一个相遇的时间。满足则出栈。
Code:
#include<bits/stdc++.h> using namespace std; typedef long long LL; typedef long double ld; typedef pair<int,int> pii; const int N = 5e4+5; const int Mod = 1e9+9; #define pi acos(-1) #define INF 1e8 #define INM INT_MIN #define dbg(ax) cout << "now this num is " << ax << endl; struct Node{ LL x,a; friend bool operator < (const Node &a,const Node &b) { if(a.a == b.a) return a.x < b.x; return a.a < b.a; } }f[N]; bool check(Node a,Node b,Node c) { return (a.x-b.x)*(c.a-b.a)-(b.x-c.x)*(b.a-a.a) <= 0; } int q[N]; int main() { int t;scanf("%d",&t); while(t--) { int n;scanf("%d",&n); map<Node,int> mp; for(int i = 1;i <= n;++i) { scanf("%lld %lld",&f[i].x,&f[i].a); mp[f[i]]++; } sort(f+1,f+n+1); int cnt = 0; for(int i = 1;i <= n;++i) { while((cnt > 0 && f[i].x >= f[q[cnt]].x) || (cnt > 1 && check(f[i],f[q[cnt]],f[q[cnt-1]]))) cnt--; q[++cnt] = i; } int ans = 0; for(int i = 1;i <= cnt;++i) { if(mp[f[q[i]]] == 1) ans++;//这里是栈内的元素判重,少些了q调了好久 } printf("%d\n",ans); } system("pause"); return 0; }
