高斯消元

我们看下面这个例题：

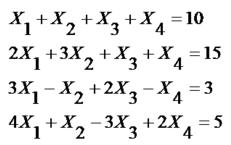
我们该如何求解方程组？
我们考虑加减消元。第j行减去第i行的元素的k倍，使得要消去的元的系数变为0（用第i行消去第j行）。
直到最后一个式子仅剩一个元，则可求出该元，再回代到前面的式子求出其他元。
这里介绍矩阵的解法：
我们将方程的系数和等式右边的数提出来，组成以下的增广矩阵：

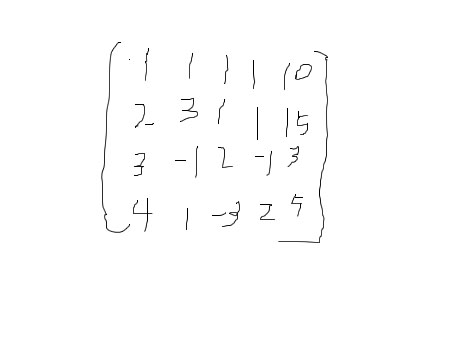
然后用矩阵的初等变换进行化简（相当于加减消元的思想）， 使其左边部分（前n列）形成一个上三角矩阵。

显然x4的值可以直接得出，带入上一个式子可求x3……一直代入上式就可求出每个元。

实现：

首先我们需要用第一列中（所有的 xx 中）系数最大的来消其他两个式子。而这里为了方便起见，我们将这个选中的系数置为 1，方便上例中地不断带回原式的操作（这样在回带的时候就可以不考虑原本的系数了）。

由于最多也只能用 double 型存储，所以必然会有精度误差。但如果我们每次都选用最大系数的来消掉其他系数，就可以最大程度地来减小误差。接着我们用这一行去消掉下面的未知数。

当我们得到了上三角矩阵，就可以进行回代了。

顺便说一下如何判断解的情况：

当增广矩阵左侧（就是元的系数）都为0，且右边的数字不全为0，那么显然是无解的

当增广矩阵全是0，显然有无穷多解。(因为x_i可以取任意值嘛)

代码实现如下：板子题

#include<iostream>//我觉得只要思维清晰，数论问题代码都是好懂的，看不明白可以结合数学的过程（数学真有趣qwq） 
#include<cstdio>
#include<algorithm>
#include<cmath>
using namespace std;
double a[110][110],ans[110];
int n;
double eps=1e-7;//这是来控制精度的，因为当一个数小于精度范围，我们是把它视为0的 
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    for(int j=1;j<=n+1;j++)
    scanf("%lf",&a[i][j]);//读入增广矩阵 
    for(int i=1;i<=n;i++)
    {
        int k=i;
        for(int j=i+1;j<=n;j++)
        if(fabs(a[k][i])<fabs(a[j][i]))//fabs（）是求double型变量的绝对值 
        k=j;                            //我们去寻找这一列中最大元素在哪一行，然后同第一行交换。 
        if(i!=k)swap(a[i],a[k]);
        if(fabs(a[i][i])<eps)
        {
            printf("No Solution");//因为a[i][i]是这一列最大的，如果它都是0，说明这一列的系数均为0。我们就求不出这个元了，故无解（或有无穷多解） 
            return 0;
        }
        double div=a[i][i];
        for(int j=i;j<=n+1;j++)a[i][j]/=div;//现将我们规定的这个数置为1 
        for(int j=1;j<=n;j++)//用这一行进行加减消元消掉其他式子中该未知数 
        {
            if(i==j)continue;
            div=a[j][i];
            for(int k=1;k<=n+1;k++)
            a[j][k]-=div*a[i][k];
        }
    }
    ans[n]=a[n][n+1];//以下是回代过程 
    for(int i=n-1;i>=1;i--)
    {
        ans[i]=a[i][n+1];
        for(int j=i+1;j<=n;j++)
        ans[i]-=ans[j]*a[i][j];
    }
    for(int i=1;i<=n;i++)printf("%.2lf\n",ans[i]);
}

 不过说实在的，这个板子的数据实在水，甚至你写错了也能过，我们还是看一个良心一点的板子题吧：

[SDOI2006]线性方程组

这道题具体考你解的情况了，你就不能No Solution后return 0；了，尽管你知道它肯定无解，你也要完成消元过程再判断解的情况了。

至于怎么判断，就像上面所说过的那样（克拉默法则）

代码如下：

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
using namespace std;
double a[110][110],ans[110];
int n;
double eps=1e-7;
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    for(int j=1;j<=n+1;j++)
    scanf("%lf",&a[i][j]);
    for(int i=1;i<=n;i++)
    {
        int k=i;
        for(int j=i+1;j<=n;j++)
        if(fabs(a[k][i])<fabs(a[j][i]))
        k=j;
        if(i!=k)swap(a[i],a[k]);
        if(fabs(a[i][i])<eps)
        continue;
        double div=a[i][i];
        for(int j=i;j<=n+1;j++)a[i][j]/=div;
        for(int j=i+1;j<=n;j++)
        {
            div=a[j][i];
            for(int k=1;k<=n+1;k++)
            a[j][k]-=div*a[i][k];
        }
    }
    int x=0;
    int y=0;
    for(int i=1;i<=n;i++)
    {
        int j=1;
        while(fabs(a[i][j])<eps&&j<=n+1)j++;
        if(j>n+1)
        x=1;//无穷多解 
        else 
        if(j==n+1)
        y=1;//无解 
    }
    if(y)
    {
        printf("-1");
        return 0;
    }
    if(x)
    {
        printf("0");
        return 0;
    }
    ans[n]=a[n][n+1];
    for(int i=n-1;i>=1;i--)
    {
        ans[i]=a[i][n+1];
        for(int j=i+1;j<=n;j++)
        ans[i]-=ans[j]*a[i][j];
    }
    for(int i=1;i<=n;i++)
    {
        cout<<"x"<<i<<"=";
        if(ans[i]==0)cout<<0<<endl;
        else
        printf("%.2lf\n",ans[i]);
    }
}

总结：高斯消元是虽然是0（n³）的算法，但还是挺有用的，至少做数学作业方便多了（逃）