279. 完全平方数

给定正整数 n，找到若干个完全平方数（比如 1, 4, 9, 16, ...）使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。

示例 1:

输入: n = 12
输出: 3 
解释: 12 = 4 + 4 + 4.

示例 2:

输入: n = 13
输出: 2
解释: 13 = 4 + 9.

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/perfect-squares

---

思路：

这题之前用BFS的方法解决过，之前也说过，在DP算法中还会遇到

DP算法，还是要总结找归类的，如果就自己去找，去发现的话还挺困难的

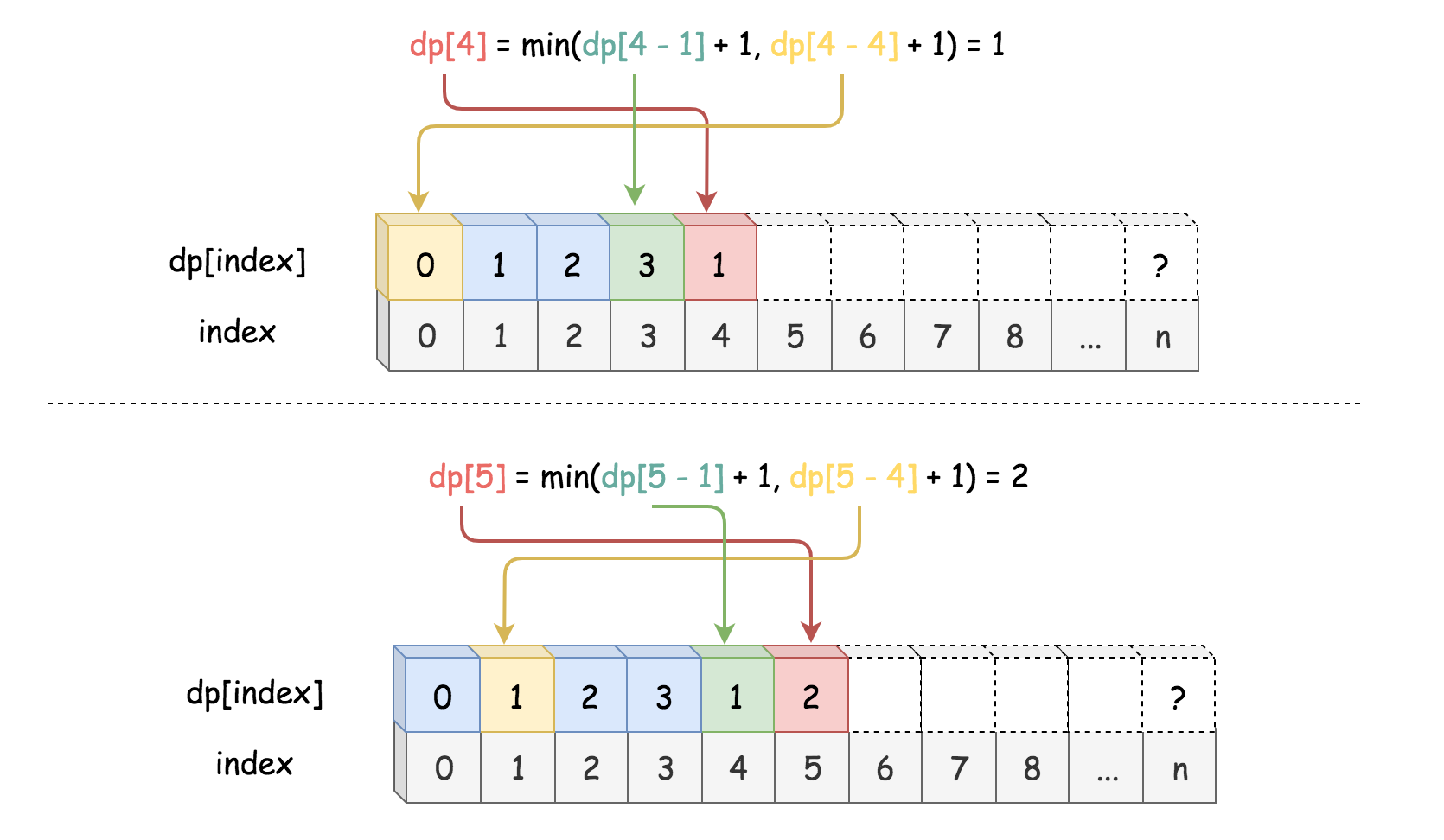
 从官方偷的图，先要找到在这个数之前的平方数有哪些，基本上的规律就是

比如图中的找4的最少个数的时候，要和dp【4 - 4】 + 1比，那么4为什么要减4

5这个再找的时候为什么也是减去了4，那如果是9呢？

9要减去1 或者 4 ，或者 9 当然除去一些不合法的

ok，那规律就是，减去小于等于他的平方数

class Solution {

  public int numSquares(int n) {
    //dp数组的长度为n + 1
        int dp[] = new int[n + 1];
        //将dp数组第一个元素设置为0，其余的都充以最大元素
        Arrays.fill(dp, Integer.MAX_VALUE);
        dp[0] = 0;

        //这里找到比n小的所有的平方数
        int maxIndex = (int) Math.sqrt(n) + 1;
        int square_nums[] = new int[maxIndex];
        for (int i = 1; i < maxIndex; ++i) {
            square_nums[i] = i * i;
        }
        
        //这里就遍历比较，后面得出来的值都建立在前面的值的基础上
        for (int i = 1; i <= n; ++i) {
            for (int s = 1; s < maxIndex; ++s) {
                if (i < square_nums[s])
                    break;
                dp[i] = Math.min(dp[i], dp[i - square_nums[s]] + 1);
            }
        }
        return dp[n];
  }
}