10.23模拟赛

T1叉叉

题目描述

现在有一个字符串，每个字母出现的次数均为偶数。接下来我们把第一次出现的字母a和第二次出现的a连一条线，第三次出现的和四次出现的字母a连一条线，第五次出现的和六次出现的字母a连一条线...对其他25个字母也做同样的操作。

现在我们想知道有多少对连线交叉。交叉的定义为一个连线的端点在另外一个连线的内部，另外一个端点在外部。

下图是一个例子，共有三对连线交叉（我们连线的时候，只能从字符串上方经过）。

 

 

输入格式

一行一个字符串。保证字符串均由小写字母组成，且每个字母出现次数为偶数次。

输出格式

一个整数，表示答案。

样例输入

abaazooabz

样例输出

3

数据范围

对于30% 的数据，字符串长度不超过50。

对于100% 的数据，字符串长度不超过100,000。

代码：

抽出线段计算覆盖

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;

char s[100009];
int ans,len,cnt,pre[30];

struct E{
    int l,r;
}e[100009];

bool cmp(E a,E b){
    return a.l<b.l;
}

int main(){
    freopen("corss.in","r",stdin);
    freopen("corss.out","w",stdout);
    scanf("%s",s+1);len=strlen(s+1);
    for(int i=1;i<=len;i++){
        int k=s[i]-'a'+1;
        if(pre[k]){
            e[++cnt].l=pre[k];
            e[cnt].r=i;
            pre[k]=0;
            continue;
        }
        pre[k]=i;
    }
    sort(e+1,e+cnt+1,cmp);
    for(int i=1;i<=cnt;i++){
        for(int j=i+1;j<=cnt;j++){
            if(e[j].l>e[i].r)break;
            if(e[j].l<e[i].r&&e[j].r>e[i].r)ans++;
        }
    }
    printf("%d
",ans);
    fclose(stdin);fclose(stdout);
    return 0;
}

对于区间[l,r]如果某个字母对于这个区间相交，那么[1,l-1]会出现奇数次，[l,r]至少出现一次。

同理[r+1,n]出现奇数次，我们只计算[1,l-1]出现奇数次。

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#define maxn 100009
using namespace std;

char s[maxn];
int ans,len,cnt,pre[30],sum[maxn][27];

struct E{
    int l,r;
}e[maxn];

bool cmp(E a,E b){
    return a.l<b.l;
}

int main(){
//    freopen("corss.in","r",stdin);
//d    freopen("corss.out","w",stdout);
    scanf("%s",s+1);len=strlen(s+1);
    for(int i=1;i<=len;i++){
        int k=s[i]-'a'+1;
        for(int j=1;j<=26;j++)sum[i][j]=sum[i-1][j];
        sum[i][k]++;
        if(pre[k]){
            e[++cnt].l=pre[k];
            e[cnt].r=i;
            pre[k]=0;
            continue;
        }
        pre[k]=i;
    }
    sort(e+1,e+cnt+1,cmp);
    for(int i=1;i<=cnt;i++){
        int l=e[i].l,r=e[i].r;
        for(int j=1;j<=26;j++){
            if(sum[l-1][j]&1)
             if(sum[r-1][j]-sum[l][j])ans++;
        }
    }
    printf("%d
",ans);
    return 0;
}

 T2　跳跳虎

 

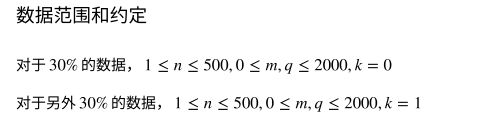
题解：

分层图最短路。dis数组开二维。dis[i][v]表示到i用了v个边。

注意k很大，然而没有什么卵用，因为q=2000.数组开2000就好了。

代码:

#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#define INF 0x3f3f3f3f
#define maxn 1000
using namespace std;

int n,m,p,q,sumedge,k,ans;
int dis[maxn][2090],inq[maxn][2090],head[maxn];

struct node{
    int x,cnt;
};
queue<node>qq;

struct Edge{
    int x,y,z,nxt,s;
    Edge(int x=0,int y=0,int z=0,int nxt=0,int s=0):
        x(x),y(y),z(z),nxt(nxt),s(s){}
}edge[maxn*5];

void add(int x,int y,int z,int s){
    edge[++sumedge]=Edge(x,y,z,head[x],s);
    head[x]=sumedge;
}

void spfa(){
    memset(dis,0x3f,sizeof(dis));
    dis[1][0]=0;inq[1][0]=true;
    node a;a.x=1;a.cnt=0;
    qq.push(a);
    while(!qq.empty()){
        node now=qq.front();qq.pop();
        inq[now.x][now.cnt]=false;
        int x=now.x,cnt=now.cnt;
        for(int i=head[x];i;i=edge[i].nxt){
            int v=edge[i].y;
            if(edge[i].s==0&&cnt<k){
                if(dis[v][cnt+1]>dis[x][cnt]+edge[i].z){
                    dis[v][cnt+1]=dis[x][cnt]+edge[i].z;
                    if(inq[v][cnt+1]==0){
                        inq[v][cnt+1]=true;
                        node nxt;nxt.x=v;nxt.cnt=cnt+1;
                        qq.push(nxt);
                    }
                }
            }
            if(edge[i].s==1){
                if(dis[v][cnt]>dis[x][cnt]+edge[i].z){
                    dis[v][cnt]=dis[x][cnt]+edge[i].z;
                    if(!inq[v][cnt]){    
                        node nxt;nxt.x=v;nxt.cnt=cnt;
                        qq.push(nxt);
                        inq[v][cnt]=true;
                    }
                }
            }
        }
    }
}

int main(){
    freopen("move.in","r",stdin);
    freopen("move.out","w",stdout);
    scanf("%d%d%d%d",&n,&m,&q,&k);
    k=min(k,q);
    //n个点，m条边，q表示通道数量，k表示能用几次。
    for(int i=1;i<=m+q;i++){
        int x,y,z;
        scanf("%d%d%d",&x,&y,&z);
        if(i>m)add(x,y,z,0);
        else add(x,y,z,1);
    }
    spfa(); 
    ans=INF;
    for(int i=0;i<=k;i++)ans=min(ans,dis[n][i]);
    if(ans==INF)printf("-1
");
    else printf("%d
",ans);
    fclose(stdin);fclose(stdout);
    return 0;
}

 T3秀秀与布鲁国