1.学习总结(2分)
1.1查找的思维导图

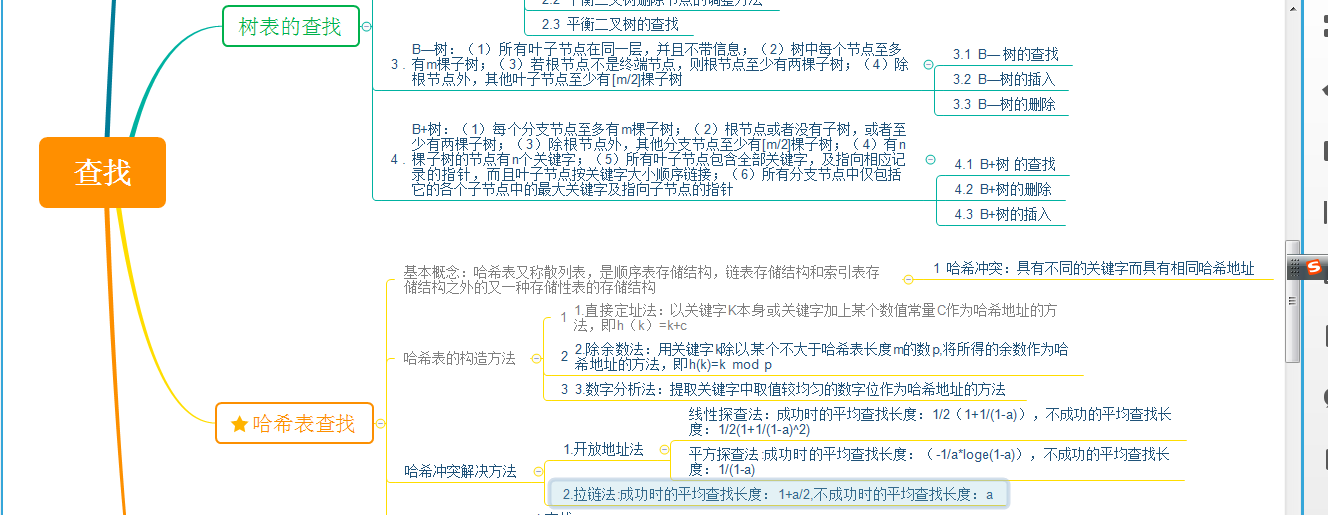

.2 查找学习体会
查找这章的内容大多是操作多于编程,很多概念如果理不清楚的话很容易出错,比如说B—和B+树的插入和删除操作,有些概念稍微有那么一点容易混淆,还有平衡二叉树的调整,删除之类的,以及哈希表的查找;还有这周学习的map函数,Map的元素是成对的键值/实值,内部的元素依据其值自动排序,Map内的相同数值的元素只能出现一次,Multimaps内可包含多个数值相同的元素,内部由二叉树实现(实际上基于红黑树(RB-tree)实现。学习这周主要用到了map函数中的find函数和count函数:
使用count,返回的是被查找元素的个数。如果有,返回1;否则,返回0。注意,map中不存在相同元素,所以返回值只能是1或0。
使用find,返回的是被查找元素的位置,没有则返回map.end()。
详细操作见链接:https://www.cnblogs.com/Deribs4/p/4948351.html
2.PTA实验作业(4分)
2.1 题目1:6-3 二叉搜索树中的最近公共祖先(25 分)

2.2 设计思路
解题思路:首先判断u,v 是否在树中,若不在,返回ERROR,若在,判断u,v是否同在树的左子树或右子树或分别在树的左右子树,然后再根据其关系找出最近公共祖先
伪代码:
Tree p;定义flag=0;
p=T;
if p不为空
if(p->Key等于u)
flag=1;break;
else if p->Key大于u
p=p->Left;
else
p=p->Right;
if flag= 0;返回ERROR
同理判断v是否在树中
p=T;
while(P不为空)
if(u,v都小于p->Key)
p=p->Left;
else if(u,v都大于p->Key)
p->Right;
else
break;
返回 p->Key;
end
2.3 代码截图


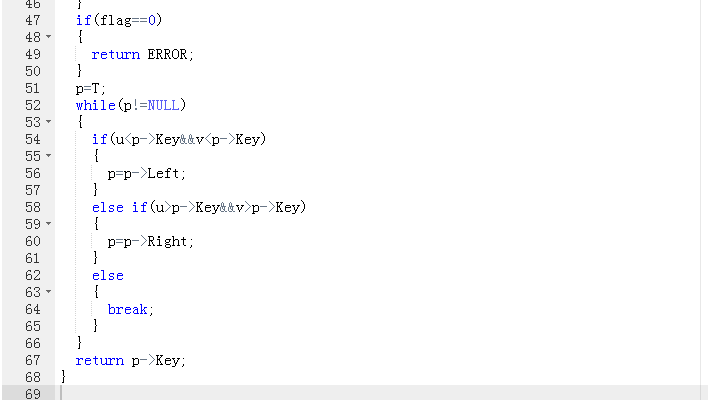
2.4 PTA提交列表说明
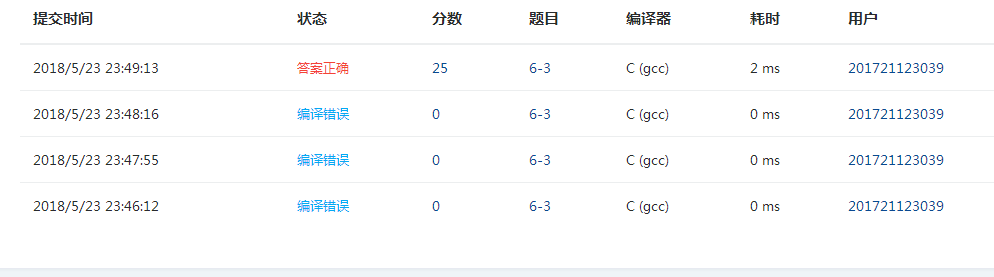
这题基本上没什么太大的问题,其做题思路呢就是:先判断u,v在树中是否存在,若不存在则返回ERROR,若存在则,判断u,v若都小于根节点,这说明在左子树上去其最近公共祖先,p=p->Left ,当满足(uKey&&v>p->Key)||(u>p->Key&&vKey)时则p->Key即为最近的公共祖先,同理当u,v若都大于根节点时,可求出在右子树上的最大公共祖先;这题只是在运行的时候不小心把定义的变量写错,导致编译错误,
2.1 题目2:7-1 QQ帐户的申请与登陆(25 分)

2.2 设计思路
解题思路:调用Map函数,若输入的命令为申请,调用T.find函数检验id,若T.find函数等于T.end,说明STL容器中没有此账号,将密码附给账号,申请成功,否则说明账号已存在;若输入命令为老账户登录,调用T.find函数检验id,若T.find函数等于T.end,说明账号输入错误,若T.find函数不等于T.end,说明账号存在,判断密码是否相等,若不等,则密码输入错误,若相等,则登录成功
伪代码
定义 M;string c,id,pass;
输入M;
while M--
输入c,id,pass;
if c[0]等于N
if(T.find(id)!=T.end())
输出 ERROR: Exist
else
T[id]=pass;
输出 New: OK
else
if(T.find(id)==T.end())
输出ERROR: Not Exist
else
if 密码匹配
输出Login: OK
else
输出ERROR: Wrong PW
2.3 代码截图
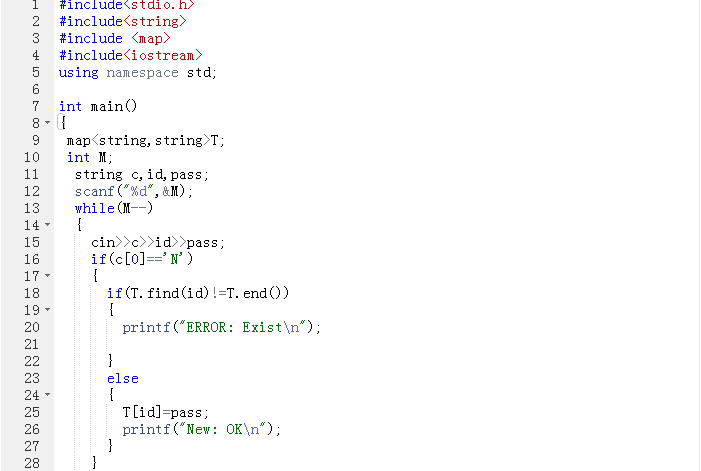
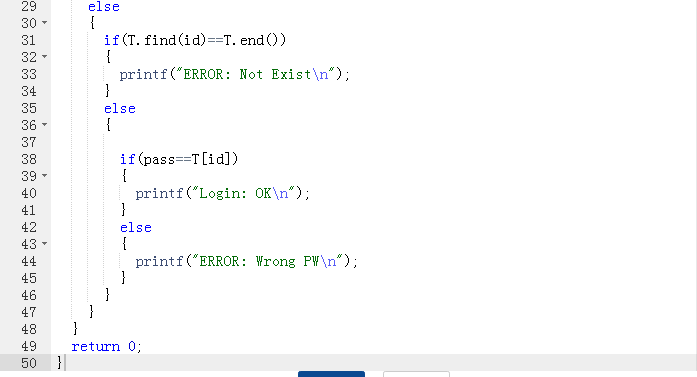
2.4 PTA提交列表说明

这题是看了老师说的调用map函数来做的,一开始的时候不理解T.find和T.end的运用,导致一直写不出来 ,然后上网百度了下T.find和T.end的用法后才写出来的,使用find,返回的是被查找元素的位置,没有则返回map.end()。 map.end()指向map的最后一个元素之后的地址,所以当输入申请的命令的时候,若T.find函数等于T.end,说明STL容器中没有此账号,将密码附给账号,申请成功,否则说明账号已存在;若输入命令为老账户登录,若T.find函数等于T.end,说明账号输入错误,若T.find函数不等于T.end,说明账号存在,判断密码是否相等,若不等,则密码输入错误,若相等,则登录成功
2.1 题目3:6-2 是否二叉搜索树(25 分)
2.2 设计思路
解题思路:判断是否二叉搜索树,需满足(1)非空左子树的所有键值小于其根结点的键值。(2)非空右子树的所有键值大于其根结点的键值。
(3)左、右子树都是二叉搜索树。,且由二叉搜索树的性质可知,左子树的最大键值在最右下角,右子树的最小键值在最左下角,故找到左子树的最大键值,小于根节点,找到右子树的最小键值,大于根节点,则为二叉搜索树
伪代码:
BinTree p;
if T不为空,返回true;
if T的左右子树都不为空,返回true
p=T->Left ;
if p不为空
while(P->Right不为空)
p=p->Right;
if P->Data大于T->Data
返回false
同理检验T的右子树
递归检验右子树和左子树是否是二叉搜索树
返回 IsBST(T->Left)&&IsBST(T->Right)
end
2.3 代码截图
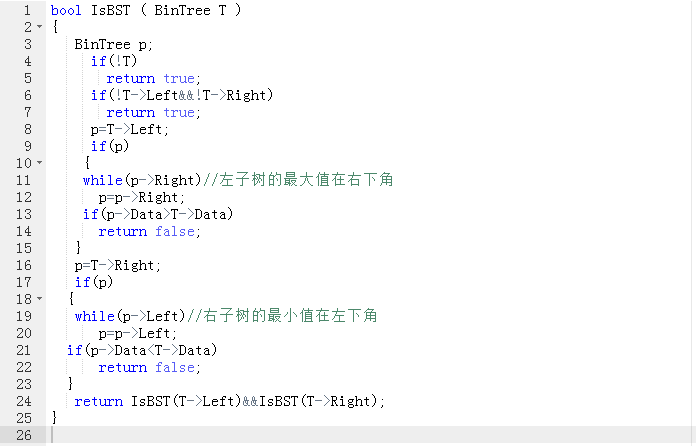
2.4 PTA提交列表说明
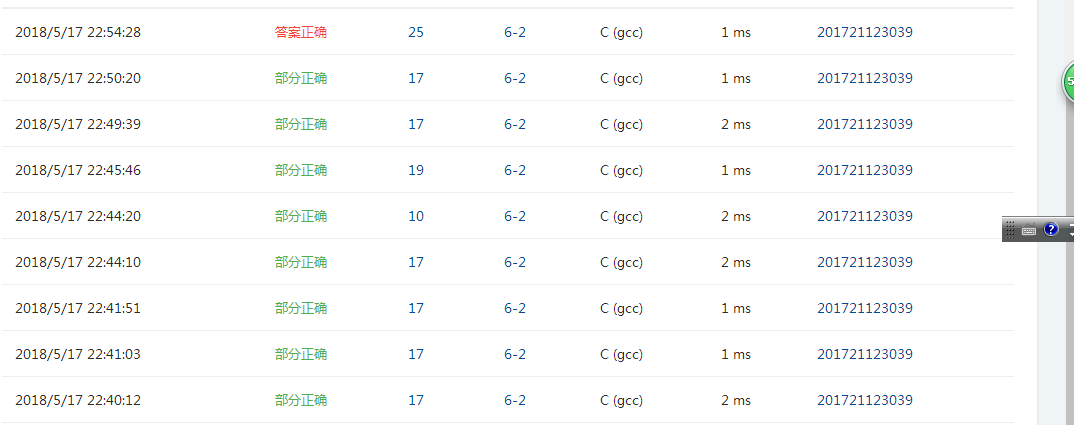
这题部分正确的原因主要是忘记判断当二叉搜索树的左右子树为空,它也是二叉搜索树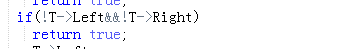 ,加上这句判断后答案正确
,加上这句判断后答案正确
3.截图本周题目集的PTA最后排名(3分)
3.1 PTA排名(截图带自己名字的排名)

3.2 我的总分:2.5
4. 阅读代码(必做,1分)
哈希表查找代码实现 -
https://blog.csdn.net/qq_35644234/article/details/68068293
详细介绍了哈希表查找的三种解决哈希冲突的方法 ,即线性探测,二次探测,链地址法,
5. 代码Git提交记录截图