zoukankan      html  css  js  c++  java

  • Unity3D 正六边形，环状扩散，紧密分布，的程序



    最近在做一个正六边形的游戏，被一开始的布局难倒了。

    需求：中心有个正六边形，输入围绕中心扩散的环数，自动创建和摆放。

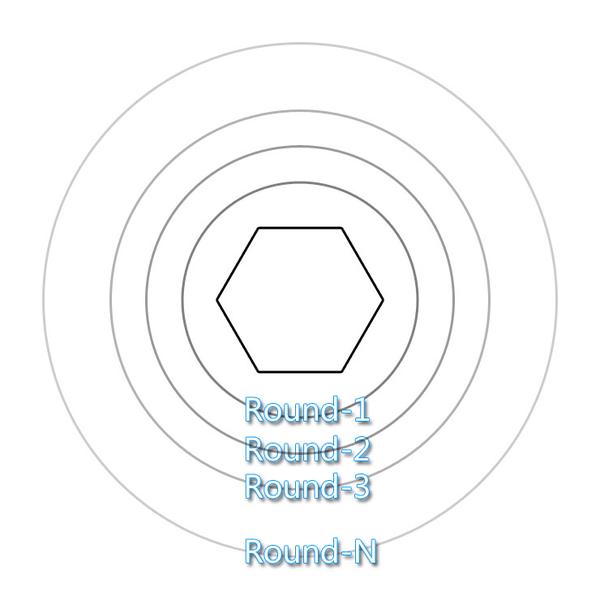
    大概就是这样的吧，我觉得这个非常轻松的就可以搞定了。啊~~~~~啊~~~ 五环~~，你比四环多一环，啊~~~~啊~~~五环~~，你比六环少一环~~~

    可是，到底每环要放多少个六边形？经过我缜密的观察发现一个规律。

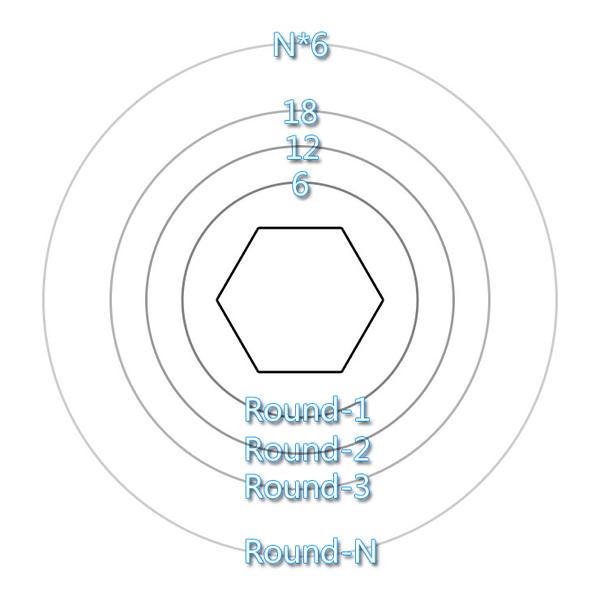
    如果假设第一个环编号为1，那么每个换六边形的数量就是 环数*6。啊~~~~~啊~~~ 五环~~，一环就是紫~禁~城~~~~。

    可是摆放的具体位置是哪里？既然是圆形，那就需要知道 角度 和 半径 就可以依据圆形坐标公式算出来了。

    二维圆上的点坐标公式:

    X = Mathf.Sin(角度*Mathf.PI/180) * 半径

    Y = Mathf.Cos(角度*Mathf.PI/180) * 半径

    有人可能问，上面写的公式原理是啥？哈~哈~哈~~~~

    啊~~~~~啊~~~ 五环~~，你比四环多一环，啊~~~~啊~~~五环~~~~~~

    参见：已知圆心，半径，角度，求圆上的点坐标 - - 博客频道 - CSDN.NET


    -----半径是啥？

    紧密摆放的话，半径就是六边形的宽度。而每一环的半径就是环数*第一个半径。

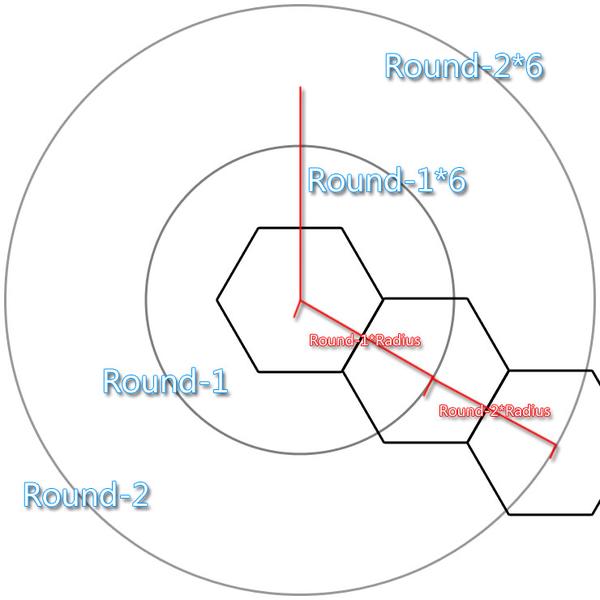
    好了这个可以大概构建一个循环体了。

    =========下面搭建循环体============

     1 Int RoundMax = 10;//最大环数变量
 2 
 3 float Radius = 1f;//六边形最短宽度
 4 
 5 for（int round = 1;round<=RoundMax;round++）//每一层环的循环体
 6 
 7 {
 8 
 9 for（环上每个六边形循环体）
10 
11 
12 Vector2 = new Vector2(Mathf.Sin(角度*Mathf.PI/180) * Radius * round, Mathf.Cos(角度*Mathf.PI/180) * Radius * round);
13 
14 }
15 
16 }

    ===============

    那么角度又是多少？

    360 ÷ 每一环的总数 = 间隔的角度

    间隔的角度 × 当前序号 = 当前角度

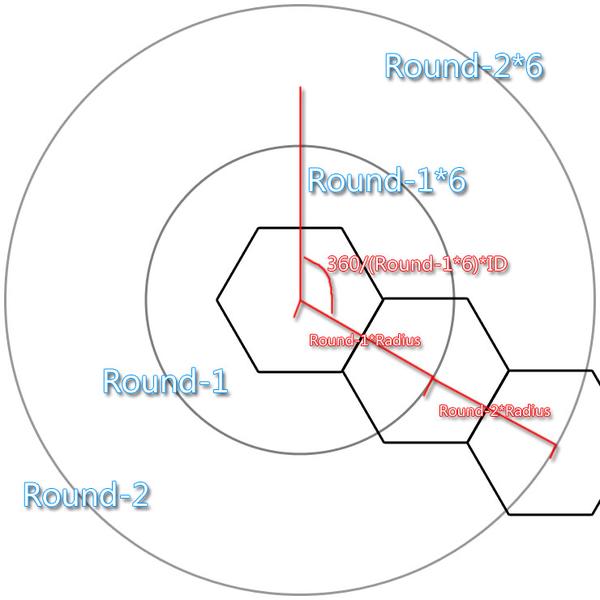
    =========下面添加每一环的计算程序============

     1 Int RoundMax = 10;//最大环数变量
 2 
 3 float Radius = 1f;//六边形最短宽度
 4 
 5 for（int round = 1;round<=RoundMax;round++）//每一层环的循环体
 6 
 7 {
 8 
 9 for（int id = 0; id<=round*6; id++）//当前环的总个数 = round*6
10 
11 {
12 
13 Vector2 Pos= new Vector2(
14 
15 Mathf.Sin(360/(round*6)*id*Mathf.PI/180) * Radius * round,
16 
17 Mathf.Cos(360/(round*6)*id*Mathf.PI/180) * Radius * round
18 
19 );
20 
21 }
22 
23 }

    =======下面转为三维向量========


     1 Int RoundMax = 10;//最大环数变量
 2 
 3 float Radius = 1f;//六边形最短宽度
 4 
 5 for（int round = 1;round<=RoundMax;round++）//每一层环的循环体
 6 
 7 {
 8 
 9 for（int id = 0; id<=round*6; id++）//当前环的总个数 = round*6
10 
11 {
12 
13 Vector3 Pos= new Vector3(
14 
15 Mathf.Sin(360/(round*6)*id*Mathf.PI/180) * Radius * round,
16 
17 0，
18 
19 Mathf.Cos(360/(round*6)*id*Mathf.PI/180) * Radius * round
20 
21 );
22 
23 }
24 
25 }

    =====距离胜利还有一步 下面引入模型和创建========

     1 GameObject Zero_OBJ;//六边形物体
 2 
 3 Int RoundMax = 10;//最大环数变量
 4 
 5 float Radius = 1f;//六边形最短宽度
 6 
 7 for（int round = 1;round<=RoundMax;round++）//每一层环的循环体
 8 
 9 {
10 
11 for（int id = 0; id<=round*6; id++）//当前环的总个数 = round*6
12 
13 {
14 
15 Vector3 Pos= new Vector3(
16 
17 Mathf.Sin(360/(round*6)*id*Mathf.PI/180) * Radius * round + ,
18 
19 0，
20 
21 Mathf.Cos(360/(round*6)*id*Mathf.PI/180) * Radius * round
22 
23 );
24 
25 Instantiate(Zero_OBJ,
26 
27 Zero_OBJ.transform.position.+ Pos ,//依据物体坐标偏移
28 
29 Quaternion.identity);
30 
31 }
32 
33 }

    =======哈哈哈 我是在佩服我的智慧========


    天空飘来五个字 那都不是事


    运行结果


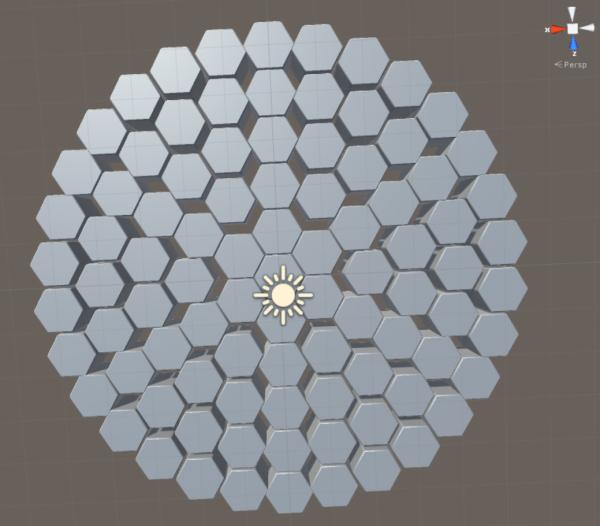
    我去~~~真圆~~~~~


    接下的十几分钟...


    =================然后开始奋发图强的思考=============

    其实还是有几个摆放正确的六边形

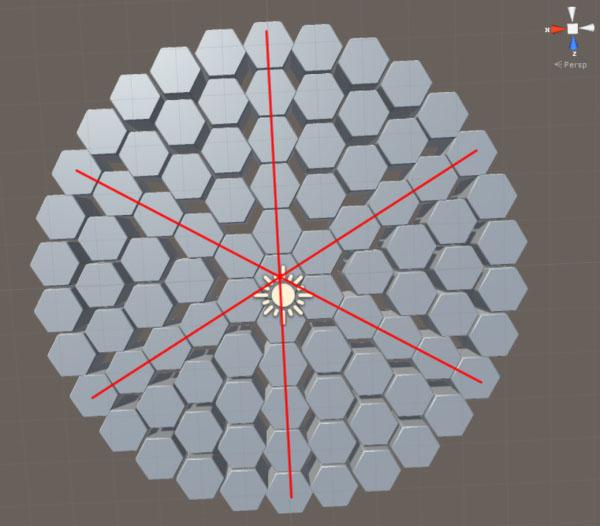
    也就是说除了这0 , 60，120 , 180 , 240 , 300 角度的六边形，其余六边形其实不是正圆分布，而是直线分布。

    如果是直线分布，就需要依据两点的坐标计算出排列的矢量方向，然后依据半径摆放就可以了。


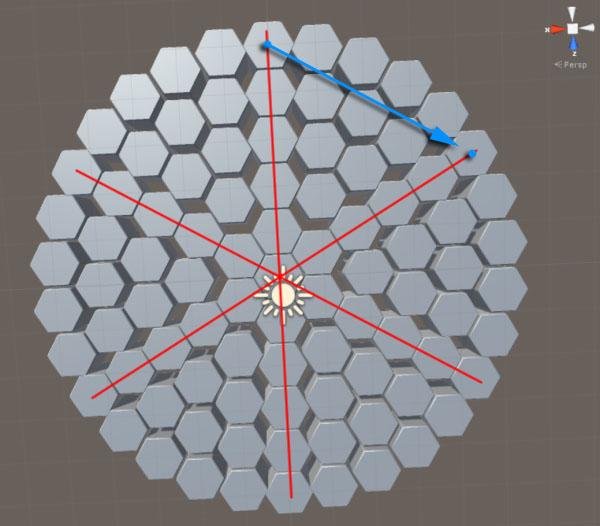
    =====接下吧正确位置写入 Pos_6[]========

     1 GameObject Zero_OBJ;//六边形物体
 2 
 3 Int RoundMax = 10;//最大环数变量
 4 
 5 float Radius = 1f;//六边形最短宽度
 6 
 7 for（int round = 1;round<=RoundMax;round++）//每一层环的循环体
 8 
 9 {
10 
11 int [] Pos_6 = new int[6]；//记录正确6个位置的数组
12 
13 for（int id = 0; id<= 6; id++）//当前环的总个数 = round*6
14 
15 {
16 
17 Vector3 Pos_6[i]= new Vector3(
18 
19 Mathf.Sin(360/(round*6)*id*Mathf.PI/180) * Radius * round + ,
20 
21 0，
22 
23 Mathf.Cos(360/(round*6)*id*Mathf.PI/180) * Radius * round
24 
25 );
26 
27 Instantiate(Zero_OBJ,
28 
29 Zero_OBJ.transform.position.+ Pos_6[i] ,//依据物体坐标偏移
30 
31 Quaternion.identity);
32 
33 }
34 
35 
36 }

    中间的六边形个数规律是：

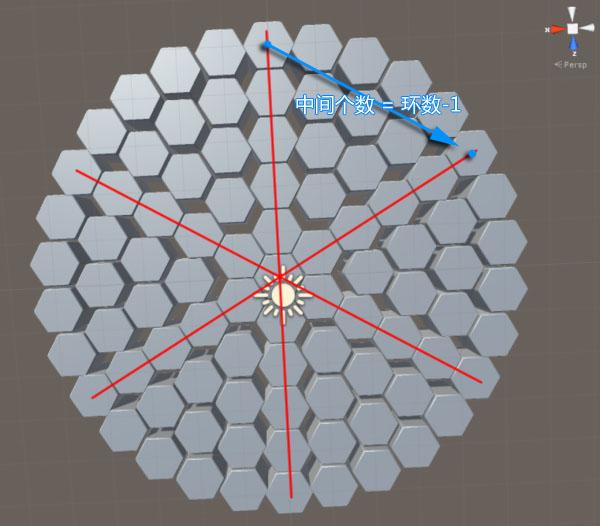
    每个六边形偏移距离是：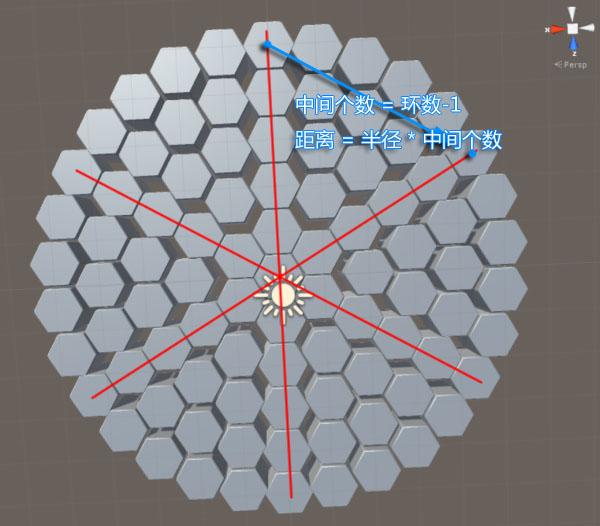


    =======接下来插入之间的六边形========


     1 GameObject Zero_OBJ;//六边形物体
 2 
 3 Int RoundMax = 10;//最大环数变量
 4 
 5 float Radius = 1f;//六边形最短宽度
 6 
 7 for（int round = 1;round<=RoundMax;round++）//每一层环的循环体
 8 
 9 {
10 
11 int [] Pos_6 = new int[6]；//记录正确6个位置的数组
12 
13 for（int id = 0; id<= 6; id++）
14 
15 {
16 
17 Vector3 Pos_6[i]= new Vector3(
18 
19 Mathf.Sin(360/(round*6)*id*Mathf.PI/180) * Radius * round + ,
20 
21 0，
22 
23 Mathf.Cos(360/(round*6)*id*Mathf.PI/180) * Radius * round
24 
25 );
26 
27 Instantiate(Zero_OBJ,
28 
29 Zero_OBJ.transform.position+ Pos_6[i] ,//依据物体坐标偏移
30 
31 Quaternion.identity);
32 
33 }
34 
35 
36 if(round >1)//第2圈开始执行插入
37 
38 {
39 
40 for（int id = 0; id<= 6; id++）//逐个区间插入
41 
42 {
43 
44 int NextID =( id+1)%6；//获取下一个位置ID，在0~5中循环取值
45 
46 
47 Vector3 Orientation = Vector3.Normalize(Pos_6[id],Pos_6[NextID])//单位朝向（当前点，上一个点）
48 
49 
50 for(int add = 0;add<round-1;add++)//循环插入
51 
52 {
53 
54 //----------插入点 = 单位方向*当前偏移距离+起点偏移
55 
56 Vector3 Now_Pos =
57 
58 Orientation
59 
60 *（Radius * add）
61 
62 +（ Pos_6[id] + Zero_OBJ.transform.position）；
63 
64 //-------------------------------------------------------------
65 
66 Instantiate(Zero_OBJ,Now_Pos,Quaternion.identity);
67 
68 
69 }
70 
71 
72 }
73 
74 }
75 
76 }

    ========运行结果===========

     
    作者：CRomputer-罗军
    链接：https://zhuanlan.zhihu.com/p/25243438
    来源：知乎
  • 相关阅读:
    DotnetCore 单文件发布
    Parallel.ForEach 之 MaxDegreeOfParallelism
    Quartznet速记
    C# SendAysnc 超时
    微耕门禁跨网段搜索代理
    服务守护DOS脚本
    Flutter速记
    ShowDoc速记
    Docker运行dotnetcore
    Redis速记
  • 原文地址：https://www.cnblogs.com/AdvancePikachu/p/6401758.html
Copyright © 2011-2022 走看看