【Silverlight】贝塞尔曲线动画（可做屏保）

先看效果：（点击可全屏）

再看整体结构：

    什么是贝塞尔曲线？请看： http://zh.wikipedia.org/wiki/%E8%B2%9D%E5%A1%9E%E7%88%BE%E6%9B%B2%E7%B7%9A

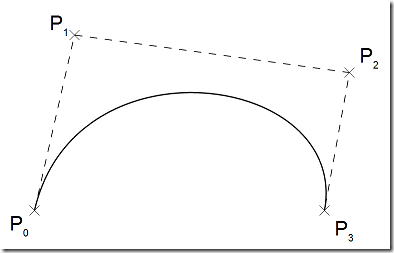
    下图演示的是四阶贝塞尔曲线的绘制过程：

    现在说说怎么用 Silverlight 产生这么漂亮的曲线。幸亏，Silverlight 已经为我们准备好了绘制曲线的接口，Path 形状。其中的 Data 属性可以使用“路径标记语法”绘制各种曲线。

    例如使用如下代码

<Canvas>
  
  <Path Stroke="DarkGoldenRod" StrokeThickness="3"
    Data="M 100,200 C 100,25 400,350 400,175 H 280"/>
</Canvas>

    可以绘制出如下图形

    现在我们需要使用路径标记语法的 C 指令绘制三阶贝塞尔曲线。C 指令需要三个点作为绘制参数。分别是 C controlPoint1 controlPoint2 endPoint。其中省略了 startPoint 点，因为起始点可以从上下文中计算出来。以下图为例，P₀ 是起始点、P₁ P₂ 是控制点、P₃是结束点。

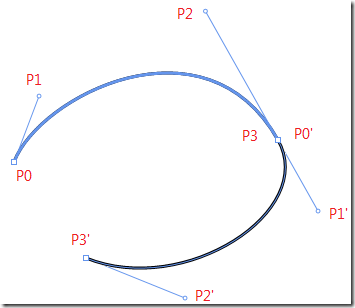
    如果绘制多段连续且光滑的贝塞尔曲线，必须要满足的条件是：前一段的 P₂-P₃ 和下一段的 P₀-P₁ 连续且共线。也就是下图的 P₃ P₀’ 必须共线、P₂-P₁’ 必须是一条直线，而不是折线。使用矢量作图工具时，默认都会让曲线满足这一条件，但是我们是要自己计算相应的点，所以在生成相应点的时候需要考虑这一条件。

    把这些关系搞清楚之后，就开始生成 Data 数据：首先 Move 到初始点，再依次用 C 绘制曲线，最后把曲线封闭了。生成 Data 数据，关键是怎样生成比较好？为了达到现在这个效果，我尝试了多种方法。现在使用的最优方法是：模拟上图中每个段的 P₂-P₁’ 端点的移送，然后在等比分点 r 确定 P₃ P₀’ 的位置。这样就变成模拟若干个点和等比分点 r 的移动问题。这里是用线性插值的方法实现颜色的缓慢变化。比较核心的代码就是 Step 方法：

        public void Step(double step)
        {
            Debug.Assert(_postion.Length == _vector.Length);
            for (int i = 0; i < _postion.Length; i++)
            {
                if (i % 3 == 0)
                {
                    int j = i - 1;
                    int k = i / 3;
                    if (j < 0) j += _postion.Length;
                    _postion[i].X = (_postion[j].X - _postion[i + 1].X) * Math.Abs(_r[k] - _splitPoint) + _postion[i + 1].X;
                    _postion[i].Y = (_postion[j].Y - _postion[i + 1].Y) * Math.Abs(_r[k] - _splitPoint) + _postion[i + 1].Y;
                    _r[k] = (_r[k] + 0.003) % (_splitPoint * 2);
                }
                else
                {
                    _postion[i].X += _vector[i].X * step;
                    _postion[i].Y += _vector[i].Y * step;

                    if (_postion[i].X < 0) _vector[i].X = Math.Abs(_vector[i].X);
                    if (_postion[i].Y < 0) _vector[i].Y = Math.Abs(_vector[i].Y);
                    if (_postion[i].X > _screenWidth) _vector[i].X = -Math.Abs(_vector[i].X);
                    if (_postion[i].Y > _screenHeight) _vector[i].Y = -Math.Abs(_vector[i].Y);
                }
            }

            var en = _postion.Select(s => new object[] { s.X, s.Y }).SelectMany(s => s);

            if (_postion.Length != 0)
            {
                string data = string.Format(_format, en.ToArray());
                SplineModel line = new SplineModel();
                line.Data = data;
                if (_currentColor >= _colorAnimation.Length)
                {
                    string name = _colorAnimation.Last();
                    double A1 = int.Parse(name.Substring(1, 2), NumberStyles.HexNumber);
                    double R1 = int.Parse(name.Substring(3, 2), NumberStyles.HexNumber);
                    double G1 = int.Parse(name.Substring(5, 2), NumberStyles.HexNumber);
                    double B1 = int.Parse(name.Substring(7, 2), NumberStyles.HexNumber);
                    name = _availableColors[Tools.NextInt(_availableColors.Length)];
                    double A2 = int.Parse(name.Substring(1, 2), NumberStyles.HexNumber);
                    double R2 = int.Parse(name.Substring(3, 2), NumberStyles.HexNumber);
                    double G2 = int.Parse(name.Substring(5, 2), NumberStyles.HexNumber);
                    double B2 = int.Parse(name.Substring(7, 2), NumberStyles.HexNumber);
                    _colorAnimation = new string[_colorInterval];
                    for (int i = 0; i < _colorInterval; i++)
                    {
                        _colorAnimation[i] = string.Format("#{0:X2}{1:X2}{2:X2}{3:X2}",
                            (int)((A2 - A1) * i / _colorInterval + A1),
                            (int)((R2 - R1) * i / _colorInterval + R1),
                            (int)((G2 - G1) * i / _colorInterval + G1),
                            (int)((B2 - B1) * i / _colorInterval + B1)
                         );
                    }
                    _currentColor = 0;
                }
                line.ColorName = _colorAnimation[_currentColor++];
                _lines.Add(line);
            }
        }

    这其中有许多细节都没有说到，需要自行阅读代码理解。至于界面是怎么设计制作的？只是使用了基本的控件布局和 VSM 而已，使用 MVVM 模式。这些不是本文讲解的重点，不太了解的可以自行查看资料理解。

完整包下载地址：https://files.cnblogs.com/Aimeast/SLBezierSpline.zip