Codeforces Round #432 Div1C. Arpa and a game with Mojtaba

C. Arpa and a game with Mojtaba

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Mojtaba and Arpa are playing a game. They have a list of n numbers in the game.

In a player's turn, he chooses a number pk (where p is a prime number and k is a positive integer) such that pk divides at least one number in the list. For each number in the list divisible by pk, call it x, the player will delete x and add 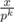 to the list. The player who can not make a valid choice of p and k loses.

Mojtaba starts the game and the players alternatively make moves. Determine which one of players will be the winner if both players play optimally.

Input

The first line contains a single integer n (1 ≤ n ≤ 100) — the number of elements in the list.

The second line contains n integers a1, a2, ..., an (1 ≤ ai ≤ 109) — the elements of the list.

Output

If Mojtaba wins, print "Mojtaba", otherwise print "Arpa" (without quotes).

You can print each letter in any case (upper or lower).

Examples

input

4
1 1 1 1

output

Arpa

input

4
1 1 17 17

output

Mojtaba

input

4
1 1 17 289

output

Arpa

input

5
1 2 3 4 5

output

Arpa

Note

In the first sample test, Mojtaba can't move.

In the second sample test, Mojtaba chooses p = 17 and k = 1, then the list changes to [1, 1, 1, 1].

In the third sample test, if Mojtaba chooses p = 17 and k = 1, then Arpa chooses p = 17 and k = 1 and wins, if Mojtaba chooses p = 17and k = 2, then Arpa chooses p = 17 and k = 1 and wins.

 思路：分析出每个数不是独立的游戏，但对于每个质因子是互不相关的。所以对每个质因子进行状态压缩，类似状压dp求出sg值，复杂度瓶颈好像在质因子分解，可以做到O(n * sqrt(MAX_A[i]) / log(MAX_A[i])。

#include <iostream>
#include <fstream>
#include <sstream>
#include <cstdlib>
#include <cstdio>
#include <cmath>
#include <string>
#include <cstring>
#include <algorithm>
#include <queue>
#include <stack>
#include <vector>
#include <set>
#include <map>
#include <iomanip>
#include <cctype>
#include <cassert>
#include <bitset>
#include <ctime>

using namespace std;

#define pau system("pause")
#define ll long long
#define pii pair<int, int>
#define pb push_back
#define mp make_pair
#define clr(a, x) memset(a, x, sizeof(a))

const double pi = acos(-1.0);
const int INF = 0x3f3f3f3f;
const int MOD = 1e9 + 7;
const double EPS = 1e-9;

int n, a[105], cnt_prim;
map<int, int> sg;
map<int, int> prim;
set<int> ss[1015];
int cal_sg(int x) {
    if (sg.count(x)) {
        return sg[x];
    }
    set<int> mex;
    for (int i = 0; i <= 30; ++i) {
        mex.insert(i);
    }
    for (int i = 1; i <= 29; ++i) {
        if ((1 << i) > x) {
            break;
        }
        int y = x;
        int mask = y >> i;
        y ^= mask << i;
        mask |= y;
        int res = cal_sg(mask);
        mex.erase(res);
    }
    return sg[x] = *mex.begin();
}
int main() {
    sg[1] = 0;
    scanf("%d", &n);
    for (int i = 1; i <= n; ++i) {
        scanf("%d", &a[i]);
        int d = sqrt(a[i] + 0.5);
        for (int j = 2; j <= d && j <= a[i]; ++j) {
            if (a[i] % j == 0) {
                int tmp = 0;
                if (!prim.count(j)) {
                    prim[j] = ++cnt_prim;
                }
                while (a[i] % j == 0) {
                    ++tmp;
                    a[i] /= j;
                }
                ss[prim[j]].insert(tmp);
            }
        }
        if (1 != a[i]) {
            if (!prim.count(a[i])) {
                prim[a[i]] = ++cnt_prim;
            }
            ss[prim[a[i]]].insert(1);
        }
    }
    int ans = 0;
    for (int i = 1; i <= cnt_prim; ++i) {
        int tmp = 0;
        for (set<int>::iterator it = ss[i].begin(); it != ss[i].end(); ++it) {
            int x = *it;
            tmp |= 1 << x;
        }
        ans ^= cal_sg(tmp);
    }
    puts(ans ? "Mojtaba" : "Arpa");
    return 0;
}