前言
自己树形dp太菜了,要重点搞
219D Choosing Capital for Treeland
终于自己做了一道不算那么毒瘤的换根dp
令 (f[u]) 表示以 (u) 为根,子树内总共需要交换的边数, (up[u]) 表示以 (u) 为根,子树外总共需要交换的边数。
Dfs1 求出 (f[u]) ,就有:
edge[u->v] 表示 u->v 这条边的方向是不是 u->v
Dfs2 求出 (up[v])(注意,是从u点求u的儿子点v),容斥一下,就有:
(+1 / -1) 是看 edge[u->v]是否等于 1,是的话就有多一条边交换方向,不是的话就要-1,因为多算了一条边
Code
#include<bits/stdc++.h>
#define INF 0x3f3f3f3f
using namespace std;
inline int read() {
int x=0,f=1; char ch=getchar();
while(ch<'0' || ch>'9') { if(ch=='-') f=-1; ch=getchar(); }
while(ch>='0'&&ch<='9') { x=(x<<3)+(x<<1)+(ch^48); ch=getchar(); }
return x * f;
}
const int N = 2e5+7;
int n,cnt;
int head[N],f[N],up[N];
struct Edge {
int next,to,flag;
}edge[N<<1];
inline void add(int u,int v,int flag) {
edge[++cnt] = (Edge)<%head[u],v,flag%>;
head[u] = cnt;
}
void Dfs1(int u,int fa) {
for(int i=head[u];i;i=edge[i].next) {
int v = edge[i].to;
if(v != fa) {
Dfs1(v,u);
f[u] += f[v] + (edge[i].flag==0); //反边
}
}
}
void Dfs2(int u,int fa) {
for(int i=head[u];i;i=edge[i].next) {
int v = edge[i].to;
if(v != fa) {
up[v] = f[u] - f[v] + up[u];
if(edge[i].flag == 1) up[v]++;
else up[v]--;
Dfs2(v,u);
}
}
}
int main()
{
n = read();
for(int i=1,u,v;i<=n-1;++i) {
u = read(), v = read();
add(u,v,1), add(v,u,0);
}
Dfs1(1,0);
Dfs2(1,0);
int ans = INF;
for(int i=1;i<=n;++i)
ans = min(ans,f[i]+up[i]);
printf("%d
",ans);
for(int i=1;i<=n;++i)
if(f[i]+up[i] == ans) printf("%d ",i);
return 0;
}
533B Work Group
这题都看了题解才会(虽然说想到了题解这个状态,但不会转移)。。。dp功力还不行啊qwq
令 (f[u][0/1]) 表示子树总和为 偶数/奇数 的最大价值(且包括根,但是根可以选或不选)
有人也许会说,奇数怎么可呢,不是说一定要偶数吗?(其实这个自己推推数据在纸上画画就差不多知道了)
像下面这张图

黑色代表选了。不选根就可以选奇数的儿子呗。转移
最后 (f[u][1]=max{f[u][1],f[u][0]+p[u]})
(1代表奇,0代表偶)1+1=0,0+0=0; 1+0=0+1=1; 这个很好理解。
可是这个 (f[u][0]) 来更新 (f[u][0]) 怎么理解呢?
其实就是前面这个 (f[u][0]) 是我们待更新的,后面这个 (f[u][0]) 是之前遍历的子树里的总最优解,意义有所不同。遍历过程中的 (f[u][0]) 稍别与(f[u][0])的定义的,只有所有更新结束后它才是u的子树选偶数个的最大值qwq。(这个不是很简单的东西吗,你怎么想了这么久啊,我确实想了这么久)
Code
#include<bits/stdc++.h>
#define INF 1e18
#define int long long
using namespace std;
inline int read() {
int x=0,f=1; char ch=getchar();
while(ch<'0' || ch>'9') { if(ch=='-') f=-1; ch=getchar(); }
while(ch>='0'&&ch<='9') { x=(x<<3)+(x<<1)+(ch^48); ch=getchar(); }
return x * f;
}
const int N = 2e5+7;
int n,cnt;
int head[N],p[N];
int f[N][2]; //f[i,0/1] 表示以i为根 子树总数是偶数/是奇数的
struct Edge {
int next,to;
}edge[N<<1];
inline void add(int u,int v) {
edge[++cnt] = (Edge)<%head[u],v%>;
head[u] = cnt;
}
void Dfs1(int u,int fa) {
//printf("QLL:: %d %d
",u,fa);
f[u][1] = -INF; //f[u,1] 开始不能是奇数
for(int i=head[u];i;i=edge[i].next) {
int v = edge[i].to;
if(v != fa) {
Dfs1(v,u);
int x0 = f[u][0], x1 = f[u][1];
f[u][0] = max(f[u][0],max(x0+f[v][0],x1+f[v][1]));
f[u][1] = max(f[u][1],max(x0+f[v][1],x1+f[v][0]));
}
}
f[u][1] = max(f[u][1],f[u][0]+p[u]);
//printf("ELL :: %d %d %d
",u,f[u][0],f[u][1]);
}
signed main()
{
n = read();
for(int i=1,u;i<=n;++i) {
u = read(); p[i] = read();
if(u!=-1) add(u,i), add(i,u);
}
Dfs1(1,0);
printf("%lld
",max(f[1][0],f[1][1]));
return 0;
}
700B Connecting Universities
挺思维的一题。从点与点的配对完全没有办法下手,从整体的考虑,一条边可以有几条路径经过,这题就迎刃而解了
假如一条边连的两个点 ((x,y)) ,(x)这边这一团的大学有 (f[x]) 座,(y)这边的这一团大学有(f[y]),我们一定要让 (min(f[x],f[y])) 座大学经过这条边与另一端的大学配对。为什么?
令 (f[x]<f[y]) 如果 (x) 这边这(f[x])个大学不去经过这条边 ((x,y)) 向另一端配对,在 (x) 这边这一端自己给自己配对,答案就不是最优,自己给自己配对没有发展,最后:
Code
#include<bits/stdc++.h>
#define int long long
using namespace std;
inline int read() {
int x=0,f=1; char ch=getchar();
while(ch<'0' || ch>'9') { if(ch=='-') f=-1; ch=getchar(); }
while(ch>='0'&&ch<='9') { x=(x<<3)+(x<<1)+(ch^48); ch=getchar(); }
return x * f;
}
const int N = 200007;
int n,m,cnt,K,ans;
int head[N],f[N];
struct Edge {
int next,from,to;
}edge[N<<1];
inline void add(int u,int v) {
edge[++cnt] = (Edge)<%head[u],u,v%>;
head[u] = cnt;
}
void Dfs(int u,int fa) {
for(int i=head[u];i;i=edge[i].next) {
int v = edge[i].to;
if(v != fa) {
Dfs(v,u); f[u] += f[v];
}
}
ans += min(f[u],K-f[u]);
}
signed main()
{
n = read(), K = read(); K <<= 1;
for(int i=1,x;i<=K;++i)
x = read(), f[x]++;
for(int i=1,u,v;i<=n-1;++i) {
u = read(), v = read();
add(u,v), add(v,u);
}
Dfs(1,0);
printf("%lld
",ans);
return 0;
}
Anton and Tree
又是一道思维难度很高的题。。。
作为提高组选手应该都能想到把一团相同颜色的点缩成一团。这个图就变成了黑白相间的一棵树。
首先这是样例里的树
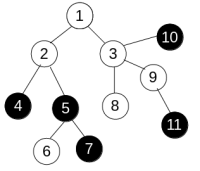
如我所说,把同色点缩成一个点就是这个样子
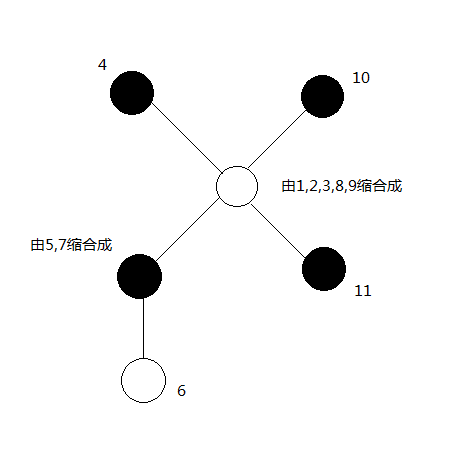
接下来就是推推结论了,(作为提高组选手应该会觉得很好推)
先给结论: 最少点击次数=(缩点后树的直径+1)/2。为什么呢?
我们不妨把直径拎出来,假设现在的直径就是下面这个图:

我们最优策略是对直径中间的一点点击一下,这样它周围的两个点就和他缩在一起了,就相当于这条链的长度-2,比如下面这张图;

因此对把直径单独拎出来最后缩成一个点的次数可以算出是 (frac{d+1}{2}) (当然这里的直径d是指边数,结果向下取整)
为什么这棵树要操作的次数就是直径要操作的次数呢?
对此,我们可以把其他点看成直径上一些点的分支,如下图:

自己手推一下直径的缩点过程,发现缩点的同时,分支也缩了一些点进去,而且,缩了一圈。进而发现这些分支会先缩完,为什么?
每缩完一个点,这个点的周围就会缩小一圈,那树上最长的一条链是什么啊?直径呗。所以比直径小的会在缩直径的同时一起缩完(这样讲能理解吧,因为我很菜,不会严格的证明,再有问题就自己手推吧)
Code
#include<bits/stdc++.h>
using namespace std;
inline int read() {
int x=0,f=1; char ch=getchar();
while(ch<'0' || ch>'9') { if(ch=='-') f=-1; ch=getchar(); }
while(ch>='0'&&ch<='9') { x=(x<<3)+(x<<1)+(ch^48); ch=getchar(); }
return x * f;
}
const int N = 200007;
int n,m,cnt,mxc,ans;
int head[N];
bool col[N];
struct Edge {
int next,to;
}edge[N<<1];
inline void add(int u,int v) {
edge[++cnt] = (Edge)<%head[u],v%>;
head[u] = cnt;
}
void Dfs(int u,int fa,int dep) {
if(dep > ans) {
mxc = u; ans = dep;
}
for(int i=head[u];i;i=edge[i].next) {
int v = edge[i].to;
if(v != fa) {
if(col[u]==col[v]) Dfs(v,u,dep);
else Dfs(v,u,dep+1);
}
}
}
int main()
{
n = read();
for(int i=1;i<=n;++i) col[i] = read();
for(int i=1,u,v;i<=n-1;++i) {
u = read(), v = read();
add(u,v), add(v,u);
}
Dfs(1,0,0);
Dfs(mxc,0,0);
printf("%d
",(ans+1)>>1);
return 0;
}