本来不是来写这题的看名字不错就顺便写了。。
连续一段长度为x的1得分为x^3，现给每个数是0或1的概率，求期望得分。n<=1e5。
方法一：f(i)--前i个数的期望得分，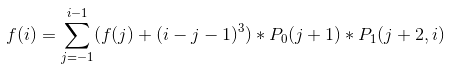
，P0表示某个数是0的概率，P1表示某段数是1的概率。
这东西不知道怎么维护？？？
方法二：新进来一个1的贡献为
，所以只要求出：最后连续x个数的期望g 和 最后连续x个数平方的期望h。
注意：辅助求的那两个东西的转移和答案转移不同，辅助的那两个期望：如果读到一个数a，有a的概率贡献g(i-1)+1、h(i-1)+2*g(i-1)+1，有(1-a)的概率贡献0；而答案是：有a的概率贡献f(i-1)+3*h(i-1)+3*g(i-1)+1，有(1-a)的概率贡献f(i-1)。
1 #include<stdio.h> 2 #include<string.h> 3 #include<stdlib.h> 4 #include<algorithm> 5 //#include<iostream> 6 using namespace std; 7 8 int n; 9 double f,ff,fff; 10 double a; 11 int main() 12 { 13 scanf("%d",&n); 14 f=ff=fff=0; 15 for (int i=1;i<=n;i++) 16 { 17 scanf("%lf",&a); 18 fff=fff+(3*ff+3*f+1)*a; 19 ff=(ff+2*f+1)*a; 20 f=(f+1)*a; 21 // cout<<fff<<endl; 22 } 23 printf("%.1f",fff); 24 return 0; 25 }