概率论与贝叶斯先验学习记录



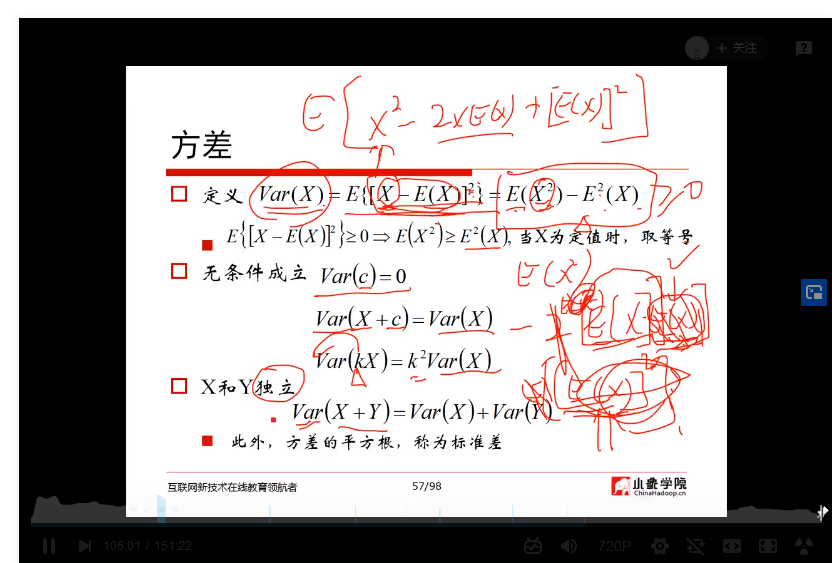
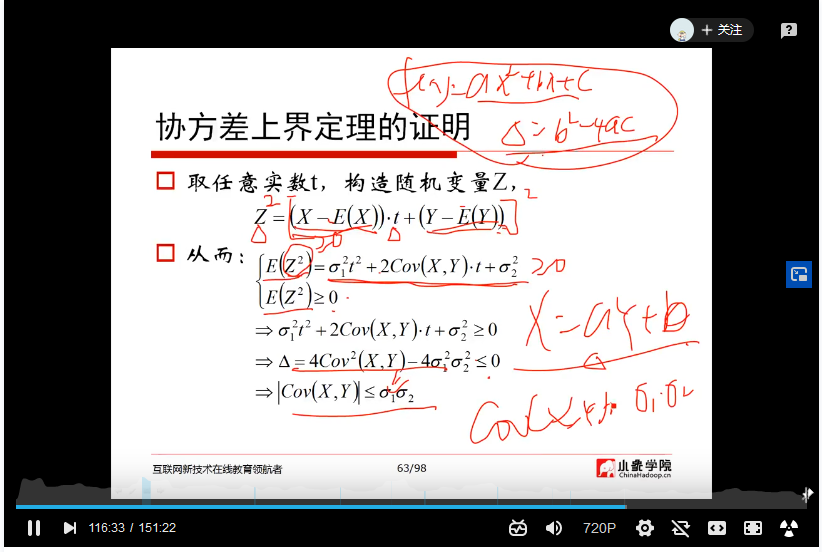
矩阵和线性代数学习记录















梯度
梯度本意是一个向量,具有向量的属性,既有方向也有大小,大小为最大方向导数,方向为沿着梯度向量的方向,最大值为梯度向量的方向,最小值为梯度向量相反的方向。
梯度下降
梯度下降是迭代法的一种,可以用于求解最小二乘问题(线性和非线性都可以),找到最小值X0,如:
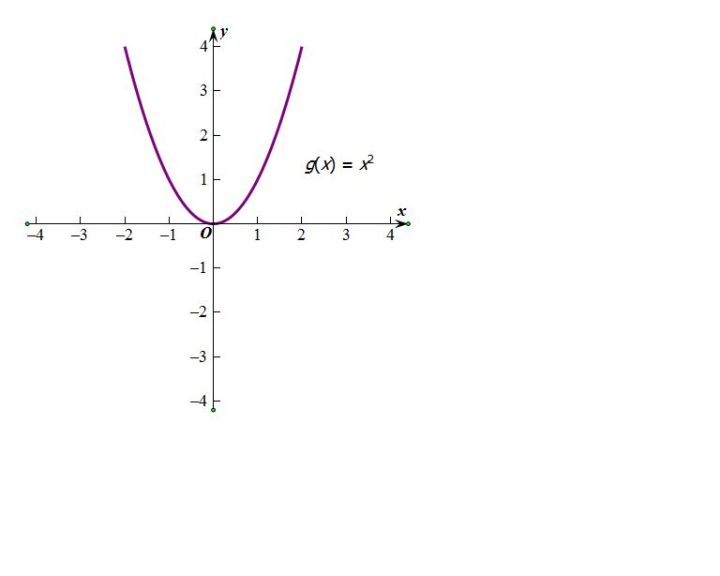
在这个简单的二次函数中,分段求取最小值,这时我们分成三段


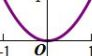
情况1:单调下降,导数为负(梯度为负),要想找到函数的最小值所对应的自变量的值(曲线最低点对应x的值)怎么走?水平向右滑,也就是让x增大,此时随着x增大,函数值是减小的(梯度下降)
情况2:单调上升,导数为正(梯度为正),要想找到函数的自变量的值(曲线最低点对应x的值)怎么走?水平向左滑,也就是让x减小,此时随着x减小,函数值减小的(梯度下降)。
综上所述:
1.梯度下降:两个意思,1.根据梯度(导数)的符号来判断最小值点x在哪; 2. 让函数值下降(变小)。
2.梯度就是导数(对于多维就是偏导数)
3.梯度下降作用是找到函数的最小值所对应的自变量的值(曲线最低点对应x的值)。
我们的目的就是找x,找到当x等于某个值时,f(x)'=0。
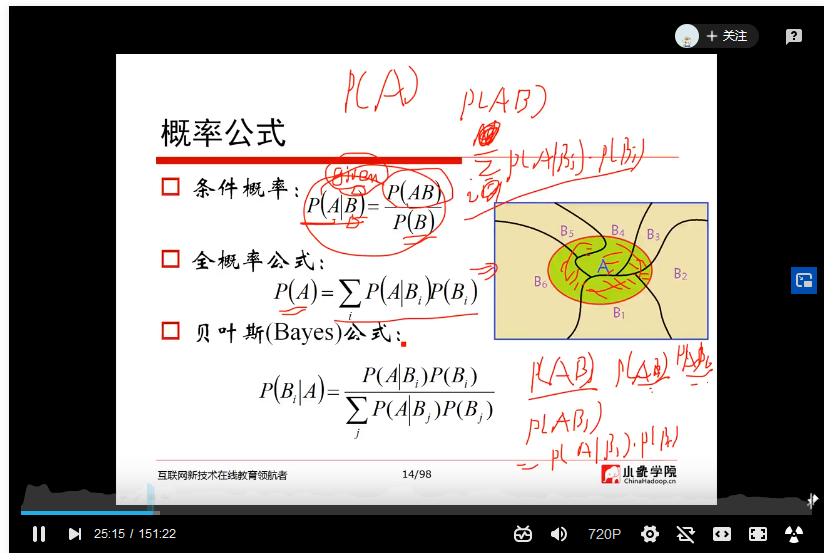
贝叶斯定理
贝叶斯定理是关于随机事件A和B的条件概率(或边缘概率)的一则定理。其中P(Bi|A)是在A发生的情况下,Bi发生的可能性。
公式为: