题目要求
题目:最大连续子数组和(最大子段和)
背景
问题: 给定n个整数(可能为负数)组成的序列a[1],a[2],a[3],…,a[n],求该序列如a[i]+a[i+1]+…+a[j]的子段和的最大值。当所给的整数均为负数时定义子段和为0,依此定义,所求的最优值为: Max{0,a[i]+a[i+1]+…+a[j]},1<=i<=j<=n
例如,当(a[1],a[2],a[3],a[4],a[5],a[6])=(-2,11,-4,13,-5,-2)时,最大子段和为20。
-- 引用自《百度百科》
一、实现代码
代码时间复杂度是O(N)
代码地址:点我。
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5 + 5;
int a[maxn];
//int dp[maxn];
//dp[i] = max{dp[i-1] + a[i],a[i]}
int solution(int a[],int n) {
int pre = 0,_max = 0;
for (int i = 0;i < n;++i) {
_max = max(_max,pre = pre > 0 ? pre + a[i] : a[i]);
}
return _max;
}
int main()
{
int n;
cin >> n;
for (int i = 0;i < n;++i) cin >> a[i];
cout << solution(a,n) << endl;
return 0;
}
/*
6
-2 11 -4 13 -5 -2
*
/
二、问题及代码分析
首先对于这个问题我们能得到:
(1)子序列必然是以正数开头的,如果以负数开头,则去掉此子序列,会得到一个更优解。
(2)一个子序列的和为负数,那么去掉这个子序列,会得到一个更优解。
下面是对此代码的具体分析过程:
1.for循环里的i变量为子序列的起点,当子序列的加和pre与a[i]的和为负时,则取为当前数字a[i],即跳到了负数和的子序列的下一个数字。
2.子序列必然是以正数开头的,如果以负数开头,则去掉此子序列,得到一个更优解。
3.一个子序列的和为负数,那么去掉这个子序列,得到一个更优解。
4._max若遇到更大的子序列和则更新。
三、单元测试
本次白箱测试选用条件组合覆盖。
其覆盖标准:使条件的每种组合至少出现一次。
程序流程图如下:
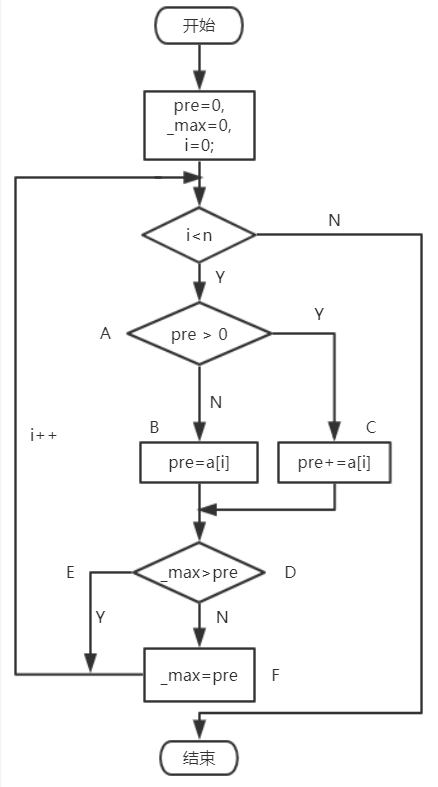
满足以下覆盖情况:
1.pre > 0;2.pre <= 0
3._max > pre;4._max <= pre
测试分析:
| 路径 | 条件组合 |
|---|---|
| ACDE | pre <= 0; _max > pre; |
| ABDE | pre > 0; _max > pre; |
| ACDF | pre <= 0; _max <= pre; |
| ABDF | pre > 0; _max <= pre; |
当n=7,测试数据为[-2,-3,11,-4,13,-5,-2]即可以对四种路径进行条件组合覆盖。
对此程序进行单元测试,具体操作过程可见此链接。
如下是测试代码:
#include "stdafx.h"
#include "CppUnitTest.h"
#include "../单元测试/test.h"
using namespace Microsoft::VisualStudio::CppUnitTestFramework;
namespace UnitTest1
{
TEST_CLASS(UnitTest1) {
public:
TEST_METHOD(Test1) {
Solution t;
int a[] = { -2,-3,11,-4,13,-5,-2 };
int n = 7;
Assert::AreEqual(20,t.solution(a,n));
}
TEST_METHOD(Test2) {
Solution t;
int a[] = { -2,-3,-5,-6};
int n = 4;
Assert::AreEqual(0, t.solution(a, n));
}
};
}
单元测试结果如下图所示: