HDU5015 233 Matrix —— 矩阵快速幂

题目链接：https://vjudge.net/problem/HDU-5015

233 Matrix

Time Limit: 10000/5000 MS (Java/Others)    Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 2805    Accepted Submission(s): 1611

Problem Description

In our daily life we often use 233 to express our feelings. Actually, we may say 2333, 23333, or 233333 ... in the same meaning. And here is the question: Suppose we have a matrix called 233 matrix. In the first line, it would be 233, 2333, 23333... (it means a_0,1 = 233,a_0,2 = 2333,a_0,3 = 23333...) Besides, in 233 matrix, we got a_i,j = a_i-1,j +a_i,j-1( i,j ≠ 0). Now you have known a_1,0,a_2,0,...,a_n,0, could you tell me a_n,m in the 233 matrix?

 

Input

There are multiple test cases. Please process till EOF.

For each case, the first line contains two postive integers n,m(n ≤ 10,m ≤ 10⁹). The second line contains n integers, a_1,0,a_2,0,...,a_n,0(0 ≤ a_i,0 < 2³¹).

 

Output

For each case, output a_n,m mod 10000007.

 

Sample Input

1 1 1 2 2 0 0 3 7 23 47 16

 

Sample Output

234 2799 72937

Hint

 

Source

2014 ACM/ICPC Asia Regional Xi'an Online

 

Recommend

hujie

题解：

假设n = 4，则矩阵中第0列元素为：

a[0][0]

a[1][0]

a[2][0]

a[3][0]

a[4][0]

根据递推，第1列为：

a[0][1] = a[0][1]

a[1][1] = a[0][1] + a[1][0]

a[2][1] = a[0][1] + a[1][0] + a[2][0]

a[3][1] = a[0][1] + a[1][0] + a[2][0] + a[3][0]

a[4][1] = a[0][1] + a[1][0] + a[2][0] + a[3][0] + a[4][0]

第m列为：

a[0][m] = a[0][m]

a[1][m] = a[0][m] + a[1][m-1]

a[2][m] = a[0][m] + a[1][m-1] + a[2][m-1]

a[3][m] = a[0][m] + a[1][m-1] + a[2][m-1] + a[3][m-1]

a[4][m] = a[0][m] + a[1][m-1] + a[2][m-1] + a[3][m-1]+ a[4][m-1]

可发现当前一列可直接由上一列递推出来，因此构造矩阵：

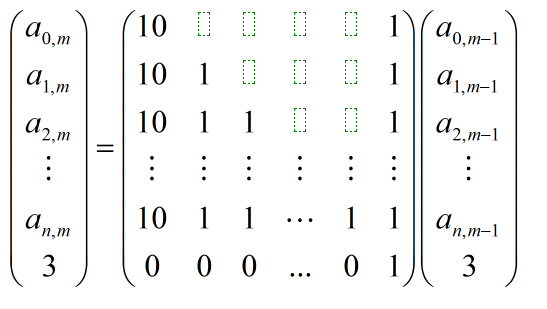
代码如下：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
#include <cmath>
#include <queue>
#include <stack>
#include <map>
#include <string>
#include <set>
using namespace std;
typedef long long LL;
const int INF = 2e9;
const LL LNF = 9e18;
const int MOD = 10000007;
const int MAXN = 1e6+100;

const int Size = 12;
struct MA
{
    LL mat[12][12];
    void init()
    {
        for(int i = 0; i<Size; i++)
        for(int j = 0; j<Size; j++)
            mat[i][j] = (i==j);
    }
};

MA mul(MA x, MA y)
{
    MA ret;
    memset(ret.mat, 0, sizeof(ret.mat));
    for(int i = 0; i<Size; i++)
    for(int j = 0; j<Size; j++)
    for(int k = 0; k<Size; k++)
        ret.mat[i][j] += (1LL*x.mat[i][k]*y.mat[k][j])%MOD, ret.mat[i][j] %= MOD;
    return ret;
}

MA qpow(MA x, LL y)
{
    MA s;
    s.init();
    while(y)
    {
        if(y&1) s = mul(s, x);
        x = mul(x, x);
        y >>= 1;
    }
    return s;
}

int main()
{
    LL n, m, a[15];
    while(scanf("%lld%lld",&n,&m)!=EOF)
    {

        for(int i = 1; i<=n; i++)
            scanf("%lld", &a[i]);
        a[0] = 23; a[n+1] = 3;

        MA s;
        memset(s.mat, 0, sizeof(s.mat));
        for(int i = 0; i<=n; i++)
        {
            s.mat[i][0] = 10;
            s.mat[i][n+1] = 1;
            for(int j = 1; j<=i; j++)
                s.mat[i][j] = 1;
        }
        s.mat[n+1][n+1] = 1;

        s = qpow(s, m);
        LL ans = 0;
        for(int i = 0; i<=n+1; i++)
            ans += 1LL*a[i]*s.mat[n][i]%MOD, ans %= MOD;

        printf("%lld
", ans);
    }
}