【Comet OJ

Description

传送门

• 在平面上给定 n 个点和一个 d，要求找到一条直线 l，使得到 l 的距离不超过 d 的点的个数最大。输出该最大点数。
  1≤n≤2000,0≤d≤10000

Solution

• 显然这条直线l往两边平移d的距离后的两条直线一定经过分别经过一个点。
• 否则就可以通过调整使其满足。
• 那么我们就可以枚举往左平移的那条线经过的点，现在要求的是经过一个点的所有直线它的右手方向2d的距离最多有多少个点。
• 刚开始我想的是这条直线一定还被另一个点限制，这样再枚举一个点就可以确定一条直线了。但是这样子并不好就算向右2d中右多少个点。
• 我们反过来考虑。
• 对于一个点，它如果要在这条直线的范围内的话，这个直线的与水平线的夹角应该在哪个范围之内。
  
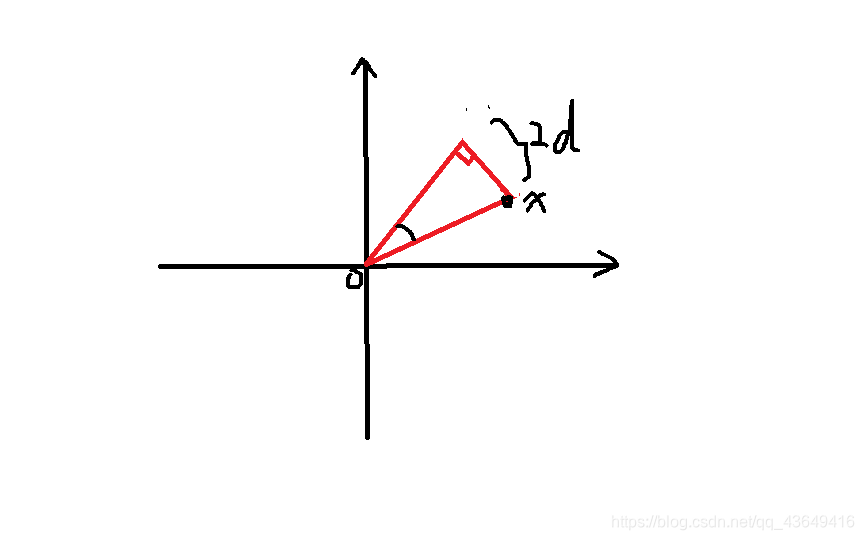
• 简单的推算后我们知道，对于与枚举的直线经过点O距离2d以外的点，在一个直角三角形的范围内可以被覆盖到。
• 相反的方向也有一个三角形，同理，因为这条直线的夹角在(0,2PI)之间
• 然后对于在2d以内的，它的贡献区间是过原点直线的一边。
• 单个点的贡献区间都是不想交的。
• 离散化之后求最大覆盖就好了。

#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
#define maxn 2005
#define db double
#define E 1e-9
using namespace std;

const db PI=acos(-1);
int n,d,i,j,k,x[maxn],y[maxn],ans,cnt,tot;
db p,q; 
struct line{
	db k; int t,fr;
} l[maxn*maxn];
int cmp(line a,line b){
	return abs(a.k-b.k)>E&&a.k<b.k || abs(a.k-b.k)<=E&&a.t>b.t;
}

db sqr(db x){return x*x;}
db dis(int i,int j){return sqrt(sqr(x[i]-x[j])+sqr(y[i]-y[j]));}

void insert(db k,int t){tot++,l[tot].k=k,l[tot].t=t,l[tot].fr=i;}
void add(db x,db y){
	if (x>=2*PI) x-=2*PI;
	if (y>=2*PI) y-=2*PI;
	if (x<=y) insert(x,1),insert(y,-1);
	if (x>y) insert(x,1),insert(2*PI,-1),insert(0,1),insert(y,-1);
}

int main(){
	scanf("%d%d",&n,&d);
	for(i=1;i<=n;i++) scanf("%d%d",&x[i],&y[i]);
	for(int s=1;s<=n;s++) {
		tot=0;
		for(i=1;i<=n;i++) if (i!=s){
			if (x[i]==x[s]) p=((y[i]>y[s])?1:-1)*PI/2; else p=atan(1.0*(y[i]-y[s])/(x[i]-x[s]));
			if (x[i]<x[s]) p+=PI;
			if (p<0) p+=PI*2;
			if (2.0*d>=dis(i,s)) 
				add(p,p+PI); 
			else {
				q=asin(2.0*d/dis(i,s));
				add(p,p+q);
				add(p+PI-q,p+PI);
			}
		}
		sort(l+1,l+1+tot,cmp);
		cnt=0;
		for(i=1;i<=tot;i++){
			cnt+=l[i].t;
			ans=max(ans,cnt);
		}
	}
	printf("%d",ans+1);
}