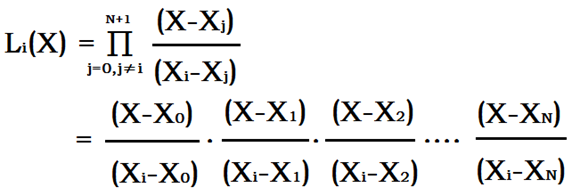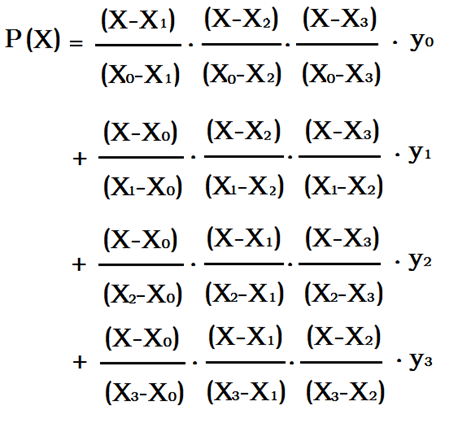插值法（内插法）

今天做题需要用到插值法, 就简单入门了一下, 同时记了一点浅显的东西于此。

定理

对于给定的 N+1 个点，存在唯一一个最高项次数不超过 N 的多项式 Y=P(X)其图像经过这N+1个点。

作用

求出的插值函数P(X)用于估计原函数F[X]。

(但如果原函数可以由多项式表示(既不是一个相关函数),且告诉了图像上其最高次项次数+1个点，就可以通过插值法得出该函数F[x],即求得的插值函数P[x]=F[x])

求法（对于给定的一组N+1个点(X₀,y₀),(X₁,y₁)......(X_N,Y_N)）

1.直接法

设出N次方程，得到N+1个线性方程，求解出多项式的系数即可。

（高斯消元哦，N³哦，很慢哦）

2.拉格朗日插值法(可以叫它构造法么？)

先构造出一组(N+1个)基函数 l₀(X) , l₁(X) , ...... , l_N(X)

使得 l_i (X)只经过(X_i , 1)，且在X=X_j ( j ≠ i )时，l_i (X_j)=0。

l_i(X)的构造如上。

显然，上式在 X=X_j ( j ≠ i )时，l_i ( X_j )=0

同时在 X=X_i 时，l_i(X_i)=1，即 y_i l_i ( X_i )=y_i

然后插值函数 P(X)即为 y_i l_i ( X ) 的线性相加：

即 P(X)=y₀ l₀ ( X )+y₁ l₁ ( X )+y₂ l₂ ( X )+……+y_N l_N ( X )

以下四个点为例：

P(X)即为我们所求的函数。

复杂度O(N²)

想要了解更多的话就看看这里：★