微平面模型
能量守恒
漫反射
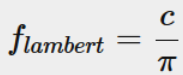
兰伯特的反照率就是一个常量,也就是albedo贴图上采样得到的值,但是和以前的兰伯特比,PBR里多除了一个PI,为什么要除呢,其实这个地方除个PI是保证能量守恒,因为我们的c是从贴图里面采样出来的,那么范围是在0到1之间的,但是实际上要能量守恒,c不能够大于PI,证明如下

反射率方程
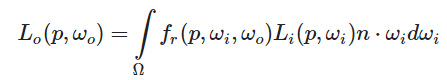
正态分布函数:估算在受到表面粗糙度的影响下,取向方向与中间向量一致的微平面的数量。这是用来估算微平面的主要函数。
几何函数:描述了微平面自成阴影的属性。当一个平面相对比较粗糙的时候,平面表面上的微平面有可能挡住其他的微平面从而减少表面所反射的光线。
菲涅尔方程:菲涅尔方程描述的是在不同的表面角下表面所反射的光线所占的比率。
数学基础-立体角


我们最好预计算这个积分,以得到像镜面 IBL 贴图这样的东西,用片段的法线对这张图采样并计算。但是,有一个地方有点棘手:我们能够预计算辐照度图,是因为其积分仅依赖于ωi,并且可以将漫反射反射率常数项移出积分,但这一次,积分不仅仅取决于ωi,从 BRDF 可以看出,这次积分还依赖ωo,我们无法用两个方向向量采样预计算的立方体图。如前一个教程中所述,位置p与此处无关。在实时状态下,对每种可能的ωi和ωo的组合预计算该积分是不可行的。 Epic Games 的分割求和近似法将预计算分成两个单独的部分求解,再将两部分组合起来得到后文给出的预计算结果。分割求和近似法将镜面反射积分拆成两个独立的积分:
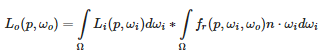
卷积的第一部分被称为预滤波环境贴图,它类似于辐照度图,是预先计算的环境卷积贴图,但这次考虑了粗糙度。因为随着粗糙度的增加,参与环境贴图卷积的采样向量会更分散,导致反射更模糊,所以对于卷积的每个粗糙度级别,我们将按顺序把模糊后的结果存储在预滤波贴图的 mipmap 中。

我们使用 Cook-Torrance BRDF 的正态分布函数(NDF)生成采样向量及其散射强度,该函数将法线和视角方向作为输入。由于我们在卷积环境贴图时事先不知道视角方向,因此 Epic Games 假设视角方向——也就是镜面反射方向——总是等于输出采样方向ωo,以作进一步近似。这样,预过滤的环境卷积就不需要关心视角方向了。翻译成代码如下:
vec3 N = normalize(w_o);
vec3 R = N;
vec3 V = R;
等式的第二部分等于镜面反射积分的 BRDF 部分。如果我们假设每个方向的入射辐射度都是白色的(因此L(p,x)=1.0 ),就可以在给定粗糙度、光线 ωi 法线 n 夹角 n⋅ωi 的情况下,预计算 BRDF 的响应结果。Epic Games 将预计算好的 BRDF 对每个粗糙度和入射角的组合的响应结果存储在一张 2D 查找纹理(LUT)上,称为BRDF积分贴图。2D 查找纹理存储是菲涅耳响应的系数(R 通道)和偏差值(G 通道),它为我们提供了分割版镜面反射积分的第二个部分:

生成查找纹理的时候,我们以 BRDF 的输入n⋅ωi(范围在 0.0 和 1.0 之间)作为横坐标,以粗糙度作为纵坐标。有了此 BRDF 积分贴图和预过滤的环境贴图,我们就可以将两者结合起来,以获得镜面反射积分的结果:
float lod = getMipLevelFromRoughness(roughness);
vec3 prefilteredColor = textureCubeLod(PrefilteredEnvMap, refVec, lod);
vec2 envBRDF = texture2D(BRDFIntegrationMap, vec2(NdotV, roughness)).xy;
vec3 indirectSpecular = prefilteredColor * (F * envBRDF.x + envBRDF.y)
预滤波HDR环境贴图
在上一节教程中,我们使用球面坐标生成均匀分布在半球 Ω 上的采样向量,以对环境贴图进行卷积。虽然这个方法非常适用于辐照度,但对于镜面反射效果较差。镜面反射依赖于表面的粗糙度,反射光线可能比较松散,也可能比较紧密,但是一定会围绕着反射向量r,除非表面极度粗糙:

所有可能出射的反射光构成的形状称为镜面波瓣。随着粗糙度的增加,镜面波瓣的大小增加;随着入射光方向不同,形状会发生变化。因此,镜面波瓣的形状高度依赖于材质。 在微表面模型里给定入射光方向,则镜面波瓣指向微平面的半向量的反射方向。考虑到大多数光线最终会反射到一个基于半向量的镜面波瓣内,采样时以类似的方式选取采样向量是有意义的,因为大部分其余的向量都被浪费掉了,这个过程称为重要性采样。
蒙特卡洛积分和重要性采样
为了充分理解重要性采样,我们首先要了解一种数学结构,称为蒙特卡洛积分。蒙特卡洛积分主要是统计和概率理论的组合。蒙特卡洛可以帮助我们离散地解决人口统计问题,而不必考虑所有人。
蒙特卡罗积分建立在大数定律的基础上,并采用相同的方法来求解积分。不为所有可能的(理论上是无限的)样本值 x 求解积分,而是简单地从总体中随机挑选样本 N 生成采样值并求平均。随着 N 的增加,我们的结果会越来越接近积分的精确结果:
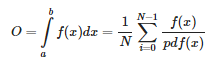
[pdf 代表概率密度函数 (probability density function)]
到目前为止,我们每次需要估算积分的时候,生成的样本都是均匀分布的,概率完全相等。到目前为止,我们的估计是无偏的,这意味着随着样本数量的不断增加,我们最终将收敛到积分的精确解。
但是,某些蒙特卡洛估算是有偏的,这意味着生成的样本并不是完全随机的,而是集中于特定的值或方向。这些有偏的蒙特卡洛估算具有更快的收敛速度,它们会以更快的速度收敛到精确解,但是由于其有偏性,可能永远不会收敛到精确解。通常来说,这是一个可以接受的折衷方案,尤其是在计算机图形学中。因为只要结果在视觉上可以接受,解决方案的精确性就不太重要。下文我们将会提到一种(有偏的)重要性采样,其生成的样本偏向特定的方向,在这种情况下,我们会将每个样本乘以或除以相应的 pdf 再求和。
蒙特卡洛积分在计算机图形学中非常普遍,因为它是一种以高效的离散方式对连续的积分求近似而且非常直观的方法:对任何面积/体积进行采样——例如半球 Ω ——在该面积/体积内生成数量 N 的随机采样,权衡每个样本对最终结果的贡献并求和。
蒙特卡洛积分是一个庞大的数学主题,在此不再赘述,但有一点需要提到:生成随机样本的方法也多种多样。默认情况下,每次采样都是我们熟悉的完全(伪)随机,不过利用半随机序列的某些属性,我们可以生成虽然是随机样本但具有一些有趣性质的样本向量。例如,我们可以对一种名为低差异序列的东西进行蒙特卡洛积分,该序列生成的仍然是随机样本,但样本分布更均匀:

当使用低差异序列生成蒙特卡洛样本向量时,该过程称为拟蒙特卡洛积分。拟蒙特卡洛方法具有更快的收敛速度,这使得它对于性能繁重的应用很有用。
鉴于我们新获得的有关蒙特卡洛(Monte Carlo)和拟蒙特卡洛(Quasi-Monte Carlo)积分的知识,我们可以使用一个有趣的属性来获得更快的收敛速度,这就是重要性采样。我们在前文已经提到过它,但是在镜面反射的情况下,反射的光向量被限制在镜面波瓣中,波瓣的大小取决于表面的粗糙度。既然镜面波瓣外的任何(拟)随机生成的样本与镜面积分无关,因此将样本集中在镜面波瓣内生成是有意义的,但代价是蒙特卡洛估算会产生偏差。
本质上来说,这就是重要性采样的核心:只在某些区域生成采样向量,该区域围绕微表面半向量,受粗糙度限制。通过将拟蒙特卡洛采样与低差异序列相结合,并使用重要性采样偏置样本向量的方法,我们可以获得很高的收敛速度。因为我们求解的速度更快,所以要达到足够的近似度,我们所需要的样本更少。因此,这套组合方法甚至可以允许图形应用程序实时求解镜面积分,虽然比预计算结果还是要慢得多。
低差异序列
本教程中,将使用重要性采样来预计算间接反射方程的镜面反射部分
该序列是把十进制数字的二进制表示镜像翻转到小数点右边而得
float RadicalInverse_VdC(uint bits)
{
bits = (bits << 16u) | (bits >> 16u);
bits = ((bits & 0x55555555u) << 1u) | ((bits & 0xAAAAAAAAu) >> 1u);
bits = ((bits & 0x33333333u) << 2u) | ((bits & 0xCCCCCCCCu) >> 2u);
bits = ((bits & 0x0F0F0F0Fu) << 4u) | ((bits & 0xF0F0F0F0u) >> 4u);
bits = ((bits & 0x00FF00FFu) << 8u) | ((bits & 0xFF00FF00u) >> 8u);
return float(bits) * 2.3283064365386963e-10; // / 0x100000000
}
// ----------------------------------------------------------------------------
vec2 Hammersley(uint i, uint N)
{
return vec2(float(i)/float(N), RadicalInverse_VdC(i));
}
无需位运算的 Hammersley 序列(见原文)
待深入:
1,split sum 证明?
2,SH原理?
3,prt工业界适用?
4,间接光,如何带颜色反射?
优先阅读:
learnopengl-cn系列
DX12渲染管线(1) - 基于物理的渲染(PBR)-moriya苏蛙可