容斥（含min-max容斥)

资料与前置知识

组合数学

博客：初探容斥原理 容斥的原理及广义应用

二项式定理

[(a+b)^n=sum_{i=0}^nC_n^ia^ib^{n-i} ]

二项式反演：

若

[f[n] = sum_{0 <= i <= n} {g[i] * c(n, i)} ]

则

[g[n] = sum_{0 <= i <= n} {f[i] * c(n, i) * (-1)^{n - i}} ]

具体见组合数学

容斥入门（小学奥数版)

容斥的基本思想：先不考虑重叠的情况，把包含于某内容中的所有对象的数目先计算出来，然后再把计数时重复计算的数目排斥出去，使得计算的结果既无遗漏又无重复

简单容斥：

[A ∩ B = A + B - A ∪ B ]

[A ∪ B = A + B - A ∩ B ]

[∪_{i = 1}^{q}A_i = sum A_i - sum {A_i ∩ A_j} + ... + (-1)^{q + 1} ∩_{i = 1}^{q}A_i ]

[∩_{i = 1}^{q}A_i = sum A_i - sum {A_i ∪ A_j} + ... + (-1)^{q + 1} ∪_{i = 1}^{q}A_i ]

这样，我们如果能够轻易知道A“并且”B的答案，就可以龟速地算出A“或者”B的答案；如果能够轻易知道A“或者”B的答案，就可以龟速地算出A“并且”B的答案

例题：

P2567 [SCOI2010]幸运数字

P1450 [HAOI2008]硬币购物

Jordan 筛法（几乎不用）

在 (n) 个集合中，选出恰好属于 (m) 个集合的元素个数：

[M_n^m = sum_{k=m}^q((-1)^{k-m}C_k^msum_{K~blong~to~Q,|K|=k}∩_{S∈K}S) ]

这涉及到了容斥的本质，见下图：（来源:qy学长的课件）

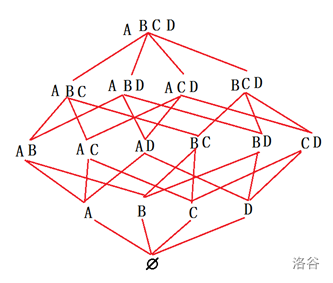
其中字母表示元素/集合，(AB) 表示 (A ∩ B) 中不属于 (C,D) 的部分，即仅属于 (A ∩ B) 的部分。

这样， (A ∩ B = AB + ABC + ABD + ABCD)（类似一个DAG上的可达点)

由于是个DAG，可以根据 (A ∩ B,A ∩ C,...) 的值来反推 (AB,AC,...) 的值。由此，可以确定容斥系数。

递推方程：“恰好”(目标） = val[cur]（递推系数） + 所有“前驱”的 val

(hard)容斥系数的确定

#2839. 集合计数

先放式子：

[C_n^k(C_{n-k}^{0}* (2^{2^{n-k}}-1) - C_{n-k}^1* (2^{2^{n-k-1}}-1)+C_{n-k}^{2}* (2^{2^{n-k-2}}-1)... ]

首先我们将交集至少为 (k) 的方案数算出来，为：(C_n^k * (2^{2^{n-k}}-1))（先确定 (k) 个数，再其它数随意）

针对我们钦定的 (k) 个数，发现多加了交集为大于等于 (k + 1) 的情况，先考虑 (k + 1)：先选出多算的那 (k + 1) 个的情况是什么情况，即选出多算了哪一个数。然后其它数任选即可。这里看似一切正常。对应的式子为 (- C_{n-k}^1* (2^{2^{n-k-1}}-1))

然后考虑交集大小为 (k + 2) 的情况：先选出多算的那两个数是哪两个数，然后考虑它已经被算了几次。(k) 的时候算了一次，两个多出来的数中每一个数都会被 (k + 1) 的时候减掉一次，这样它被算了 (1 - C_2^1) 次。看似毫无规律的样子...不过，经过化简，我们发现它被算了-1次，而它的目标系数为0，那么我们把它加一下就好了。这里已可以窥探出一些规律。对应的式子为 (+C_{n-k}{2}* (2^{2^{n-k-2}}-1))

然后考虑交集大小为 (k + 3) 的情况：照常套路，但是我们要知道它已经被算了多少次。k的时候被加了一次，然后三个多出来的数中 每一个数 都会被 (k + 1) 减掉一次，然后 每两个数 都会被 (k + 2) 加上一次。注意到“每x个数”，我们想到了基础容斥的那种情况。换言之，它被算了 (C_3^0 - C_3^1 + C_3^2) 次。看它不爽，加上个 (-C_3^3)，为 (C_3^0 - C_3^1 + C_3^2 - C_3^3)，这玩意恰恰等于0（组合恒等式），并且0恰好为目标系数。那么只需加上个 (-C_3^3) 的容斥系数就好了。规律可见，是加是减取决于当前 (k + x) 中x的奇偶。因此得出上面的式子。

容斥基础 （雾）

（小热身）

有一个集合S，如果枚举它的每个子集，即:（其中 $sum[T] $ 表示集合T内元素值的和）

[sum_{T|S=S}{sum[T]} ]

那么每个元素的贡献为：（枚举含x的集合大小）

[val[x]sum_{i=1}^{|S|}{C(|S|-1, i-1)} ]

考虑每个元素的贡献时 min-max 容斥证明的常用思想。

min-max容斥：

min-max容斥

t为s的非空子集, (min(s)) 表示集合中元素最小值， (max(s)) 表示集合中元素最大值：

[max(s)=sum{min(t)* (-1)^{|t|+1}} ]

[min(s)=sum{max(t)* (-1)^{|t|+1}} ]

当 (|s|=1) 时很好理解；

当 (|s|=2) 时也很好理解：比如s={1, 5}，那么 (max(1, 5)=1+5-min(1,5))， (min(1, 5)=1+5-max(1, 5))

当 (|s|=3) 时或许也还行：比如s={2, 3, 5}，那么

[max(1, 3, 5)=1+3+5-min(1, 3)-min(3, 5)-min(1, 5)+min(1, 3, 5) ]

[=1+3+5~ ~ ~-1-3-1~ ~ ~+1 ]

[min(1, 3, 5)=1+3+5-max(1, 3)-max(3, 5)-max(1, 5)+max(1, 3, 5) ]

[=1+3+5 ~ ~ ~ -3 - 5 - 5~ ~ ~ + 5 ]

当 (|s|>3) 时就要背结论了。

---

以 (max(S)=sum{min(T)* (-1)^{|T|+1}}) 为例：

我们要求一个函数 (f(x))，使得：

[max(S) = sum{min(T)f(|T|)} ]

考虑每个数 （第 x + 1 大） 的贡献次数：

[ismx(x)=sum_{i=0}^{x}C(x,i)f(i+1) ]

二项式反演：

[f(x+1)=sum_{i=0}^{x}{C(x,i)ismx(i)(-1)^{x-i}} ]

由于 (ismx(i)=[i==0])，因此：

[f(x+1)=C(x,0)(-1)^{x}=(-1)^x ]

即

[f(x)=(-1)^{x-1} ]

所以

[max(S) = sum{min(T)(-1)^{|T|-1}} ]

---

对于期望min-max也同样适用，即：

[E(max(s))=sum{E(min(t))* (-1)^{|t|+1}} ]

[E(min(s))=sum{E(max(t))* (-1)^{|t|+1}} ]

其中

(E(max(s))) 表示 s 集合内随机变量（期望几次能出现某元素） 的最大值，即期望几次能取完 s 集合；

(E(min(s))) 表示 s 集合内随机变量（期望几次能出现某元素） 的最小值，即期望取几次能包含 s 的一部分，即第一次取到s集合中元素的期望次数。

它的应用见下一道例题：

例题：P3175 [HAOI2015]按位或

题解 P3175 【[HAOI2015]按位或】

大概需要知道：

• min-max定理

• 若对于随机变量x：(k>0,k为整数）

[P(x == k)= (1-p)^{k-1}p ]

则有：

[E(x)=sum_{i=1}^{inf}{iP(x==i)} ]

[E(x)=psum_{i=1}^{inf}{i * (1-p)^{i-1}} ]

[E(x)=frac{1}{p} ]

最后一步等比数列乘等差数列 可以用错位相减法推出。

好像称之为：离散随机变量的几何分布（见题解）

因为 “某集合元素出现的期望最小值” 这个随机变量只能取正整数（尽管它的期望不是），因此是“离散随机变量”，可以套用这个公式。

• FWT_or搞子集问题

Code:

read(n); All = (1 << n) - 1; limi = All + 1;
for (register int i = 0; i <= All; ++i) {
	scanf("%lf", &A[i]);
}
FWT_or(A);
init_ct();
double res = 0;
for (register int s = 1; s <= All; ++s) {
	if (F(1.0 - A[All ^ s]) <= eps)	failed(s);
	res += 1.0 / (1.0 - A[All - s]) * (ct[s] & 1 ? 1 : -1);
}
printf("%.12lf
", res);

例题：喂鸽子

求 (E(max_{i in S}(x_i)))，其中 (x_i) 表示到 (i) 吃饱所需次数。设随机变量 (X) 表示出现饱鸽子的时间。

[egin{aligned} &E(max_{i in S}(x_i))\ &= sum_{T in S,T ot= phi}(-1)^{|T|+1}E(min_{i in T}(x_i))\ &= sum_{T in S,T ot= phi}(-1)^{|T|+1} sum_{k}k imes P(X=k)\ &= sum_{T in S,T ot= phi}(-1)^{|T|+1} sum_{k ge 0}P(X>k)\ &= sum_{T in S,T ot= phi}(-1)^{|T|+1} frac{|S|}{|T|}sum_{k ge 0}frac{1}{|T|^k}[frac{x^k}{k!}](sum_{i le K}frac{x^i}{i!})^{|T|}\ &= sum_{t ge 1}(-1)^{t+1}{n choose t}frac{n}{t}sum_{k=0}^{tK} frac{f_t(k)}{t^k} end{aligned}]

其中 (f_t(k) = [frac{x^k}{k!}](sum_{i le K}frac{x^i}{i!})^t)

kthmin-max（扩展min-max）

先直接抛出结论：

[kthmax(S)=sum{min(T)~* ~C(|T|-1,k-1)~* ~(-1)^{|T|-k}} ]

[kthmin(S)=sum{max(T)~* ~C(|T|-1,k-1)~* ~(-1)^{|T|-k}} ]

---

证明

以 (kthmax(S)=sum{min(T)~* ~C(|T|-1,k-1)~* ~(-1)^{|T|-k}}) 为例：

我们要 求一个函数 (f(x))，使得：

[kthmax(S) = sum{min(T)f(|T|)} ]

考虑每个数 （第 (x + 1) 大） 的贡献次数：

[iskthmx(x)=sum_{i=0}^{x}C(x,i)f(i+1) ]

二项式反演：

[f(x+1)=sum_{i=0}^{x}{C(x,i)~* ~iskthmx(i)~* ~(-1)^{x-i}} ]

由于 (iskthmx(i)=[i==k-1])，因此：

[f(x+1)=C(x,k-1)~* ~(-1)^{x-k-1} ]

即

[f(x)=C(x-1,k-1)~* ~(-1)^{x-k} ]

所以

[kthmax(S) = sum{min(T)~* ~C(|T|-1,k-1)~* ~(-1)^{|T|-k}} ]

---

记忆：你看T是大写的，那么就把 |T| 当作比 k 大的数，然后C（-1，-1）和 ^(|T|-k) （大雾）

• 扩展min-max也可以用到期望中去，即：

[E(kthmax(S))=sum{E(min(T))~* ~C(|T|-1,k-1)~* ~(-1)^{|T|-k}} ]

[E(kthmin(S))=sum{E(max(T))~* ~C(|T|-1,k-1)~* ~(-1)^{|T|-k}} ]

于是就有了下面的例题：

P4707 重返现世

每个单位时间，这片地域就会随机生成一种原料。每种原料被生成的概率是不同的，第 i 种原料被生成的概率是 (frac{p_i}{m}) 如果 Yopilla 没有这种原料，那么就可以进行收集。

Yopilla 急于知道，他收集到任意 k 种原料的期望时间，答案对 998244353 取模。

[1<=n<=1000,1<=k<=n,|n-k|<=10 ]

[0<=p_i<=m,sum p=m,1<=m<=10000 ]

---

题目要 求： ((n-k+1)thmax(All))

将 (n-K+1) 用 (K) 来表示，此时 (K <= 11)，套用期望kthmin-max公式：

[E(Kthmax(S))=sum{E(min(T))~* ~C(|T|-1,K-1)~* ~(-1)^{|T|-K}} ]

其中(P(min(T))=frac{sum p_t}{m})，每次只选一个，因此(E(min(T))=frac{1}{P(min(T))}=frac{m}{sum{p_t}})，（其中 (p_t) 为 (T) 中元素 (t) 的概率）。

发现 (n,m,K) 很小，可以考虑以这些为状态做dp。

设 (f[i][k][j]) 表示只考虑前 i 个，的 (E(kthmax(S_i))) 的式子中的(E(min(T))=frac{m}{sum{p_t}}=frac{m}{j}) 时的 (C(|T|-1,k-1)~* ~(-1)^{|T|-k})的值（因为这样同分母，好算好转移）。

这样，最终答案为：(sum_{j=1}^{m} ({frac{m}{j}~* ~f[n][K][j]}))

考虑转移。

如果第i个元素不加入所谓 (T) 集合中，那么继承前 (i-1)个：(f[i][k][j] = f[i - 1][k][j])；

剩下考虑第 (i) 个元素加入所谓 (T) 集合中：

发现 (f[i][k][j]) 只能从 (f[i-1][?][j-p_i]) 中转移而来。我们再看一下式子：

[E(Kthmax(S))=sum{E(min(T))~* ~C(|T|-1,K-1)~* ~(-1)^{|T|-K}} ]

如果加上个 (i) ，那么就变成了：

[E(Kthmax(S))=sum{E(min(T))~* ~C(|T|-1 + 1,K-1)~* ~(-1)^{|T| + 1-K}} ]

(-1) 的指数加1还好，只是正负变一下，但组合数变一下就不大妙了。但我们根据杨辉三角（或许是），即 (C(n, m) = C(n - 1, m - 1) + C(n - 1, m)) ，这样就可以拆掉了。

[sum{E(min(T))~* ~(C(|T|-1,k - 1) + C(|T|-1,k-2))~* ~(-1)^{|T| + 1-k}} ]

[=sum{E(min(T))~* ~C(|T|-1,k - 1)~* ~(-1)^{|T| + 1-k}} ]

[+ sum{E(min(T))~* ~C(|T|-1,k - 2)~* ~(-1)^{|T|-k}} ]

[=-f[i-1][k][j-p_t]+f[i-1][k-1][j-p_t] ]

总递推式为：

[f[i][k][j]=f[i-1][k][j]-f[i-1][k][j-p_t]+f[i-1][k-1][j-p_t] ]

发现复杂度可行。第一维可以滚动数组优化，也可以用类似背包一样的做法优化。

最后说一下边界：(f[0][0][0] = 0; for (k:1->m) f[0][k][0]=-1) 至今未想通。。。

(思维量与代码量不成正比）

(Code:)

for (register int i = 1; i <= K; ++i)	f[i][0] = -1;
for (register int i = 1; i <= n; ++i) {
	for (register int j = m; j >= p[i]; --j) {
		for (register int k = K; k; --k) {
			f[k][j] = (f[k][j] + f[k - 1][j - p[i]] - f[k][j - p[i]]) % P;
			if (f[k][j] < 0)	f[k][j] += P;
		}
	}
}
ll ans = 0;
for (register int j = 1; j <= m; ++j) {
	ans = (ans + f[K][j] * quickpow(j, P - 2)) % P;
}
printf("%lld
", ans * m % P);

Continued...