线性回归的总结:https://www.cnblogs.com/pinard/p/6004041.html
一、线性回归:hθ(x(i))=θ0+θ1x(i) ,x(i) ,y(i) 为观察样本值,hθ(x(i))为预测的y(i) 的值。θ为参数
可以用最小二乘法来求解线性回归:最小二乘法:其目标函数 J(θ)=1/2 ∑ ( y(i) - hθ(x(i)) )2 → J(θ)=1/2 ∑ ( y(i) - θ0 -θ1x(i) )2
最小二乘法求解:
dJ(θ0)=0与dJ(θ1)=0结合可以求出θ0和θ1
二、线性回归的正则化
线性回归常常会过拟合,所以需要考虑正则化项。
(1)Lasso回归:(正则化项为1范数)
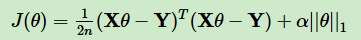
L1正则化的项有一个常数系数αα来调节损失函数的均方差项和正则化项的权重。
Lasso回归的求解办法一般有坐标轴下降法(coordinate descent)和最小角回归法( Least Angle Regression)
(2)岭回归(Ridge回归):(正则化项为2范数)
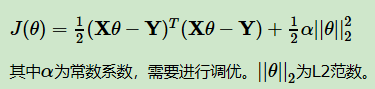
最小二乘法也可以用来求解岭回归。
三、线性回归的推广:
多项式回归(x平方、三次方等)
广义线性回归(比如LnY与X符合线性回归,不是Y和X是直接的线性关系)
四、7种回归技术:
1、线性回归【拟合直线】
2、逻辑回归【分类】
3、多项式回归【拟合曲线】
4、逐步回归【在处理多个自变量时,我们可以使用这种形式的回归。在这种技术中,自变量的选择是在一个自动的过程中完成的,其中包括非人为操作。】
5、岭回归【正则化项为2范数】
6、lasso回归【正则化项为1范数】
7、ElasticNet回归【岭回归和lasso回归的结合,它使用L1来训练并且L2优先作为正则化矩阵。当有多个相关的特征时,ElasticNet是很有用的。Lasso 会随机挑选他们其中的一个,而ElasticNet则会选择两个。】
【其中,5、6、7是回归的正则化项】
回归正则化方法(Lasso,Ridge和ElasticNet)在高维和数据集变量之间多重共线性情况下运行良好。