HDU1143（3*N的地板铺1*2的砖）

Tri Tiling

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 3004    Accepted Submission(s): 1687

Problem Description

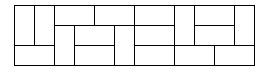
In how many ways can you tile a 3xn rectangle with 2x1 dominoes? Here is a sample tiling of a 3x12 rectangle.

 

Input

Input consists of several test cases followed by a line containing -1. Each test case is a line containing an integer 0 ≤ n ≤ 30. 

 

Output

For each test case, output one integer number giving the number of possible tilings. 

 

Sample Input

2

8

12

-1

 

Sample Output

3

153

2131

 

Source

University of Waterloo Local Contest 2005.09.24

 

思路详见：动态规划

我的代码：

const int maxn = 40;

int dp[maxn][5];

void init() {
    dp[0][0] = dp[0][2] = 1;
    dp[0][1] = 0;
    dp[1][0] = dp[1][2] = 0;
    dp[1][1] = 1;
    for (int i = 2; i <= 30; i ++) {
        dp[i][0] = dp[i-2][0] + dp[i-1][1] + dp[i-2][2];
        dp[i][1] = dp[i-1][2];
        dp[i][2] = dp[i-1][1] + dp[i][0];
    }
}

int main() {
    int n;
    init();
    while (~scanf("%d", &n)) {
        if (n == -1) break;
        printf("%d
", dp[n][0]);
    }
    return 0;
}

Discuss里的代码：

const int MAX=31;
int s[MAX];
int main()
{
    int i,n;
    s[0]=1;
    s[2]=3;
    for(i=4;i<MAX;i+=2)
    {
        s[i]=4*s[i-2]-s[i-4];
    }
    while(cin>>n,n>=0)
    {
        if(n&1)
            cout<<0<<endl;
        else
            cout<<s[n]<<endl;
    }
    return 0;
}