可持久化并查集

这个其实和可持久化线段树关系很大，算是比较具体的应用了

维护一个普通的并查集，我们只需要一个$fa$数组，然后每次$Find$的时候路径压缩，简短方便

但是当需要维护历史版本的时候，就有一些区别了

模板题：洛谷 P3402 

假设我们先不进行路径压缩，而是简单的构造一个裸的并查集，那么问题就变成维护有历史版本的$fa$数组了：这是可持久化数组的裸题

问题就在于，可持久化线段树的优秀的复杂度有一个比较严格的要求：每次修改只能是点修改

而我们考虑路径压缩的过程，发现我们在一次$Find$操作的同时，被改变$fa$值的元素可能不止一个，例如下图

如果我们在黑色的$Union$关系的基础上添加一个红色的关系，可以发现$5$->$4$的路径是有待压缩成$5$->$1$的

如果多次合并后，可能会出现比较可怕的情形：

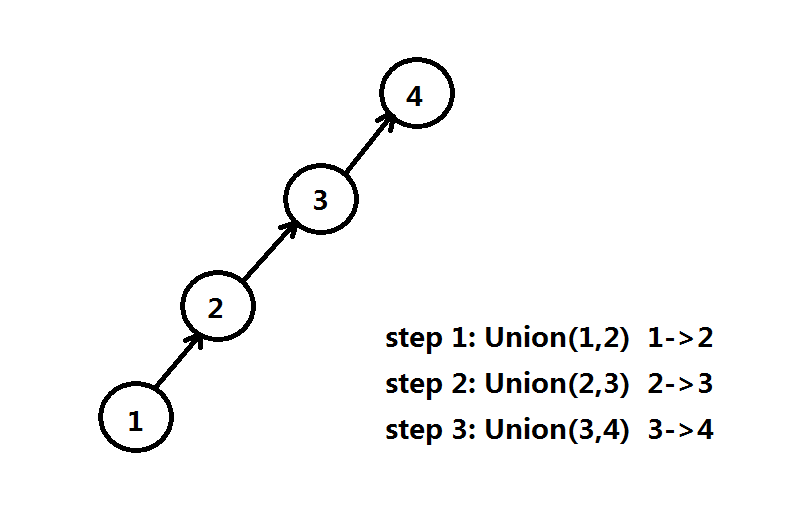
树有可能退化成一条链（因为我们连边的方法确定），在某次$Find$叶子节点的时候，可能一下路径压缩了好几次

一开始我觉得好像也不会有什么问题：路径压缩的次数跟$Union$的次数一样

但是仔细一想，如果不断回到这个版本连续$Find$，一共路径压缩的次数是$N^2$的，在时间空间上都是无法接受的

而在普通的并查集中，路径压缩的正确性在于，压缩后是一劳永逸的 这就是可持久化问题的痛苦之处

现在我们终于想起了另一种降低并查集层数的方法了：按秩合并，即根据 以当前节点为根的子树 的深度进行有方向的连边

比如，如果以$a$为根的子树深度为$d+1$、以$b$为根的子树深度为$d+2$，那么连一条$a$->$b$的边，整体的深度仍为$d+2$

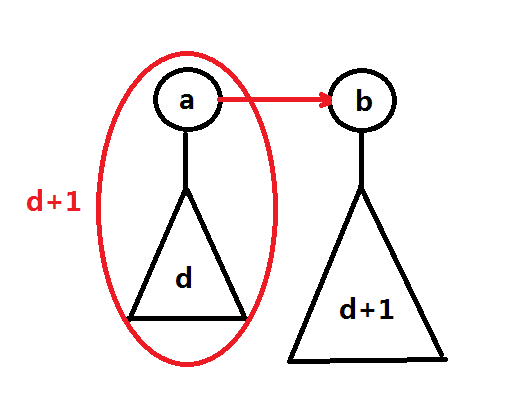
这样就跟$AVL$树在原理上很类似了，整体上树的深度是$logN$级别的

我们可以在记录$fa$数组的同时，引入$lv$数组来记录深度，这样一来，每次$Union$的时候，我们仅会进行一次连边，对应着可持久化数组的一次点修改

【在此停顿】

事实上，我们在一次$Union$的时候不仅会进行一次$fa$上的点修改，同时被连边的点有可能会$lv+1$（当$lv_a==lv_b$的时候，不管如何都会改变被连边点的子树深度）

不过，可持久化数组的一个元素$i$ 应该是包含$l_i$、$r_i$、$fa_i$和$lv_i$的一个$struct$，所以$fa$和$lv$上的修改仍可视为一次可持久化数组上的点修改，只不过需要拆分成两步

1. 修改$fa_x$
2. 修改$lv_x$

但是只有当这两步都完成的时候，才是$Union$后的历史版本

代码在$Union$的部分稍显丑陋...不知道怎么改进

#include <cstdio>
#include <cstring>
#include <cmath>
#include <iostream>
using namespace std;

const int MAX=100005;

int n,m;

int tot,sz=1;
int root[MAX*2];
int l[MAX*60],r[MAX*60],fa[MAX*60],lv[MAX*60];

void Build()
{
    root[0]=1;
    while(sz<n)
        sz<<=1;
    
    for(int i=1;i<sz;i++)
        l[i]=(i<<1),r[i]=(i<<1)+1;
    for(int i=1;i<=n;i++)
        fa[i+sz-1]=i,lv[i+sz-1]=1;
    tot=(sz<<1)-1;
}

inline int Locate(int k,int p,int a,int b)
{
    if(a==b)
        return k;
    
    int mid=(a+b)>>1;
    if(p<=mid)
        return Locate(l[k],p,a,mid);//#1: Misuse k<<1 / (k<<1)+1 instead of l[k] / r[k]
    else
        return Locate(r[k],p,mid+1,b);
}

inline int Query(int x,int p)
{
    int f=fa[Locate(root[x],p,1,sz)];
    if(f==p)
        return p;
    return Query(x,f);
}

inline void Change(int idx,int k,int p,int a,int b)
{
    if(a==b)
        return;
    
    int mid=(a+b)>>1;
    if(p<=mid)
    {
        r[idx]=r[k];
        l[idx]=++tot;
        Change(l[idx],l[k],p,a,mid);
    }
    else
    {
        l[idx]=l[k];
        r[idx]=++tot;
        Change(r[idx],r[k],p,mid+1,b);
    }
}

inline void Union(int idx,int x,int a,int b)
{
    a=Query(x,a);
    b=Query(x,b);
    if(a==b)
    {
        root[idx]=root[x];
        return;
    }
    
    int lp=Locate(root[x],a,1,sz),rp=Locate(root[x],b,1,sz);
    int p=(lv[lp]>=lv[rp]?b:a),nlv=max(lv[lp],lv[rp])+(lv[lp]==lv[rp]);
    
    int tmp=++tot;
    Change(tmp,root[x],p,1,sz);
    fa[tot]=a+b-p,lv[tot]=min(lv[lp],lv[rp]);
    root[idx]=++tot;
    Change(tot,tmp,a+b-p,1,sz);
    fa[tot]=a+b-p,lv[tot]=nlv;
}

int main()
{
//    freopen("input.txt","r",stdin);
    scanf("%d%d",&n,&m);
    Build();
    
    int cur=0,cnt=0;
    for(int i=1;i<=m;i++)
    {
        int op,x,y;
        scanf("%d",&op);
        
        if(op==1)
        {
            cnt++;
            scanf("%d%d",&x,&y);
            Union(cnt,cur,x,y);
            cur=cnt;
        }
        if(op==2)
        {
            scanf("%d",&x);
            root[++cnt]=root[x];
            cur=x;
        }
        if(op==3)
        {
            scanf("%d%d",&x,&y);
            printf("%d
",Query(cur,x)==Query(cur,y));
            root[++cnt]=root[cur];
            cur=cnt;
        }
    }
    return 0;
}

暂时不知道有什么实际用途，先学着就是了

（完）