机器学习---吴恩达---Week1（机器学习概述与单变量线性回归方程分析）

机器学习概述

Machine Learning: Grew out of work in AI & New capability for computers

Examples: Database Mining、Computer Vision、Natural Language Processing(NLP)、Self-customizing programs and so on

What is Machine Learning?

Arthur Samuel (1959)---Field of study that gives computers the ability to learn without being explicitly programmed.(事例：对象棋程序进行大量重复实战训练，提高程序战胜自己的概率)

Tom Mitchell (1998)---A computer program is said to learn from experience E with respect to some task T and some performance measure P, if its performance on T, as measured by P, improves with experience E.（典型定义，需要区分对应场景的经验、任务和测量值的对应对象，例如垃圾邮件的分类训练）

机器学习的分类：

Supervised learning（监督学习） & Unsupervised learning（非监督学习） 

Others: Reinforcement learning（强化学习）, recommender systems（推荐系统）.

Supervised learning

在确定结果的数据输入下，对连续值问题的回归问题分析和队离散值问题的分类问题分析。

Unsupervised learning

未经已知结果的数据训练，直接分析大量数据内部存在的聚类或者类似鸡尾酒会问题。

线性回归问题分析

Model representation

问题描述：

数学表达过程：

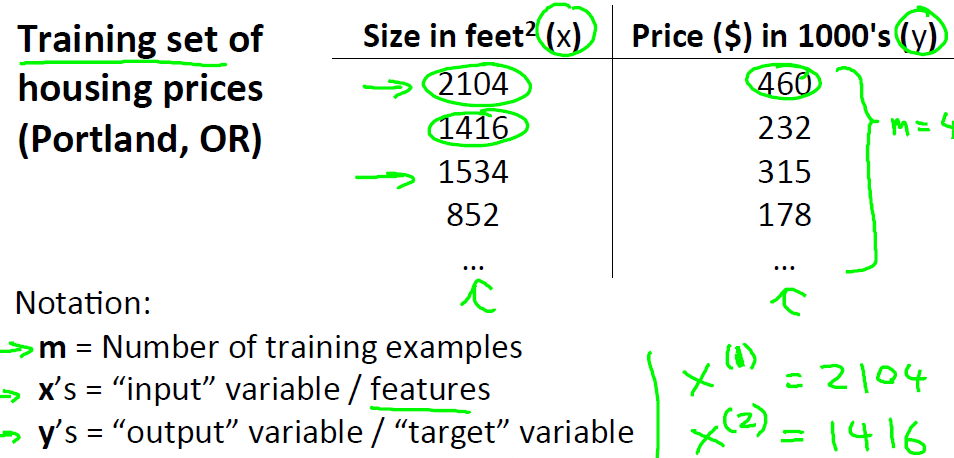
模型建立：

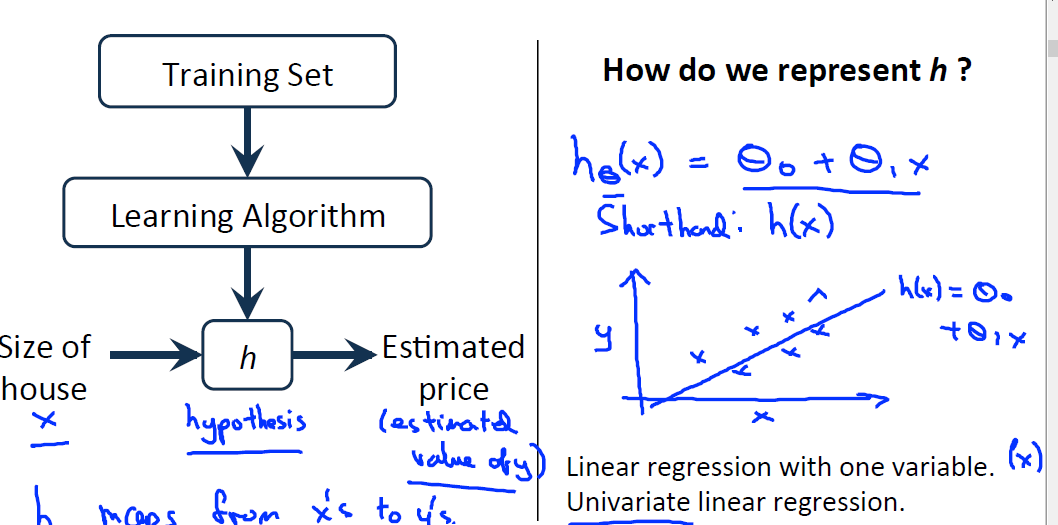
 Hypothesis（假设预测函数）

h_θ(x) = θ₀+θ₁x

其中x为特征数据输入，θi(i=1,2)为参数，结果输出为预测值。

Cost Function（损失函数）

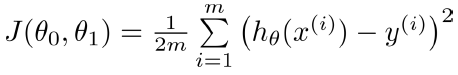
Goal

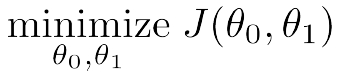
两种表现形式：

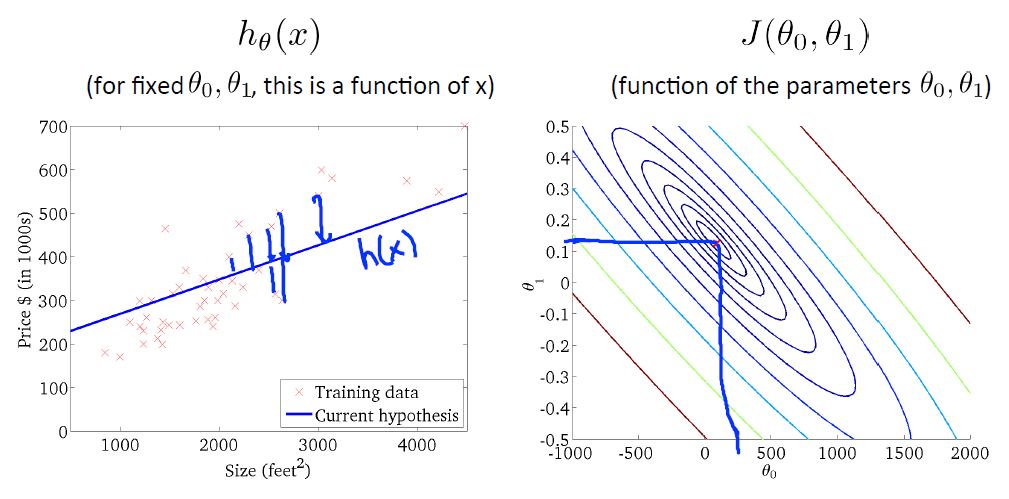
J-θ图

 等高线图：

Gradient descent（梯度离散）

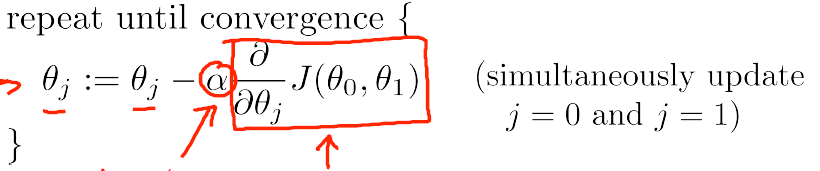
1. 对参数的同时更新
2. alpha取值过大可能会出现收敛失败的情况，J-θ图会出现上升，及损失函数发散，或出现大范围波动，取值过小，导致收敛过慢
3. As we approach a local minimum, gradient descent will automatically take smaller steps. So, no need to decrease α over time. 

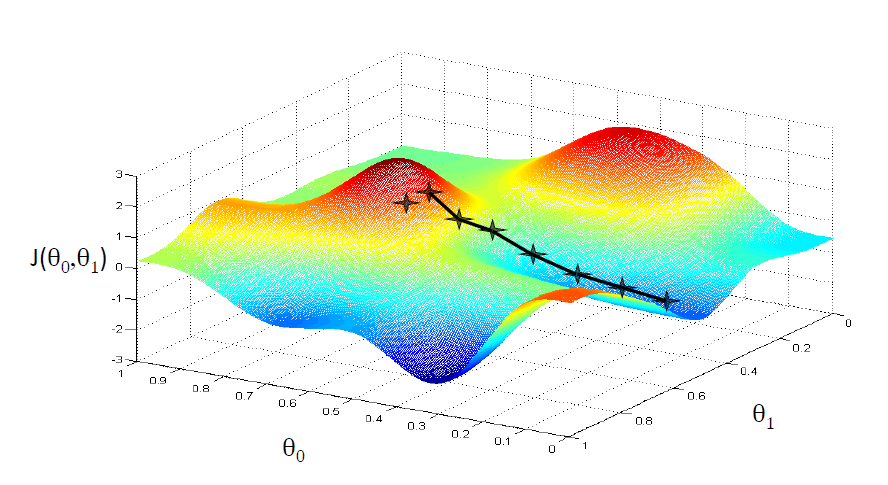
Batch Gradient descent（批量梯度离散）

 梯度离散计算过程需要使用批量的训练数据。

线性代数回顾

矩阵与向量

Matrix: Rectangular array of numbers.使用大写字母表示(e.g. 矩阵A )

Dimension of matrix: 矩阵的行数×矩阵的列数

Matrix Elements: 矩阵的每一个数据

向量：一个n×1矩阵，使用小写字母表示（e.g.y）

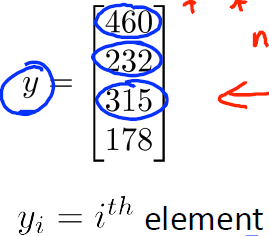
矩阵的运算

同一维度的矩阵之间可以直接相加相减，对应位置元素完成操作；

矩阵的标量乘是标量与矩阵的每一个元素进行乘或除操作，结果位置不变；

矩阵与矩阵（包括向量）的乘法如下，其一般不满足标量乘法间的交换律，可以满足标量乘的结合律。

特殊矩阵

Index Martix(单位矩阵): 左上-右下对角线位置元素全为1而其余位置元素全为0的矩阵。任意矩阵与单位矩阵相乘结果仍为其自身。

转置矩阵：矩阵的行列元素互换形成的新矩阵。

逆矩阵：求与自身矩阵相乘结果为单位矩阵的过程，称为求矩阵的逆矩阵。少数特殊矩阵不含有逆矩阵，称为对角矩阵或简并矩阵。