概
以往的\(\ell_1\)攻击, 为了保证
\[\|x' - x\|_1 \le \epsilon, x' \in [0, 1]^d,
\]
其是通过两步投影的方式完成的, 即
\[x' = P_H \circ P_{B_1 (x; \epsilon)} (u).
\]
其中\(B_1\)表示1范数球, 而\(H\)表示\([0, 1]^d\)的空间.
本文直接
\[x' = P_S (u), \: S := H \bigcap B_1 (x; \epsilon).
\]
主要内容
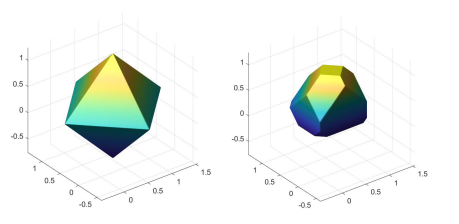
上图展示了1范数球和\(S\), 可以发现, 差别还是很大的.
正因如此, 和\(\ell_{\infty}, \ell_2\)不同, 基于二步投影的\(\ell_1\)攻击非常低效.
于是乎, 作者直接投影到\(S\), 即考虑如下的优化问题:
\[\min_{z} \: \|z - u\|_2^2 \\
\mathrm{s.t.} \: \|z - x\|_1 \le \epsilon, \: z \in [0, 1]^d.
\]
不妨令\(\tilde{w} = z - x\), 则
\[\min_{\tilde{w}} \: \|\tilde{w} - (u - x)\|_2^2 \\
\mathrm{s.t.} \: \|\tilde{w}\|_1 \le \epsilon, \: \tilde{w} + x \in [0, 1]^d.
\]
再令\(w = \mathrm{sign}(u-x) \tilde{w}\), 此时有
\[\min_{w} \: \|w - |u - x|\|_2^2 \\
\mathrm{s.t.} \: \|w\|_1 \le \epsilon, \: \mathrm{sign}(u-x)w+ x \in [0, 1]^d.
\]
显然, \(w\)非负(否则徒增消耗罢了).
为此, 我们可以归结为上述问题为下述类型问题:
\[\min_{z} \: \frac{1}{2}\|z - |u|\|_2^2 \\
\mathrm{s.t.} \: \sum_i z_i \le \epsilon, \: z_i \ge 0, \: \mathrm{sign}(u)z + x \in [0, 1]^d.
\]
约束条件可以进一步改写为
\[\sum_i z_i \le \epsilon, \\
z_i \in [0, \gamma_i], \\
\gamma_i = \max \{-x\mathrm{sign} (u), (1 - x)\mathrm{sign}(u) \}.
\]
注: 这是从这篇论文中学到的一个很有趣的技巧:
\[\begin{array}{ll}
& a \le \mathrm{sign}(u)z + x \le b \\
\Leftrightarrow&
\mathrm{sign}(u) a \le z + \mathrm{sign}(u) x \le \mathrm{sign}(u)b \\
or & \mathrm{sign}(u) b \le z + \mathrm{sign}(u) x \le \mathrm{sign}(u)a \\
\Leftrightarrow&
z \in [(a - x)\mathrm{sign}(u), (b - x)\mathrm{sign}(u)].
\end{array}
\]
下面通过拉格朗日乘子法求解(既然是个凸问题, 假设\(\gamma > 0\)):
\[\mathcal{L}(z;\lambda; \alpha; \beta) = \frac{1}{2} \|z - |u|\|_2^2 + \lambda (\sum_i z_i - \epsilon) - \alpha^Tz + \beta^T (z - \gamma).
\]
由此可得KKT条件:
\[\nabla_{z_i}\mathcal{L} = (z_i - |u_i|) + \lambda - \alpha_i + \beta_i = 0; \\
\lambda (\sum_i z_i - \epsilon) = 0; \\
\alpha_i z_i = 0, \beta_i (z_i - \gamma_i) = 0; \\
\lambda, \alpha_i, \beta_i \ge 0.
\]
故
\[z_i = |u_i| - \lambda + \alpha_i - \beta_i.
\]
我们再来具体分析:
1.
\[\beta_i \not = 0
\Rightarrow z_i = \gamma_i > 0 \Rightarrow \alpha_i = 0.
\]
故
\[\beta_i = \max(0, |u_i| - \gamma_i - \lambda).
\]
\[\alpha_i \not = 0 \Rightarrow z_i = 0 \Rightarrow \beta_i = 0.
\]
故
\[\alpha_i = \max(0, \lambda - |u_i|).
\]
于是
\[z_i=\left\{
\begin{array}{ll}
0, & \lambda > |u_i| \\
|u_i| - \lambda, & |u_i| - \gamma_i \le \lambda \le |u_i| \\
\gamma_i, & \lambda < |u_i| - \gamma_i.
\end{array}
\right .
\]
其中\(\lambda\)是下列方程的解:
\[\lambda (\sum_i z_i - \epsilon) = 0.
\]
其有一个特殊的表达方式:
\[z_i = \max(0, \min(\gamma_i, |u_i| - \lambda)).
\]
故
\[\lambda (\sum_i \max(0, \min(\gamma_i, |u_i| - \lambda)) - \epsilon) = 0.
\]
若\(\lambda=0\)时:
\[\sum_i \max(0, \min(\gamma_i, |u_i| - \lambda)) \le \epsilon,
\]
则此时\(\lambda=0\)恰为最优解, 否则需要通过
\[\sum_i \max(0, \min(\gamma_i, |u_i| - \lambda)) = \epsilon,
\]
求解出\(\lambda\).
因为\(\sum_i \max(0, \min(\gamma_i, |u_i| - \lambda))\)关于\(\lambda\)是单调递减的, 作者给了一个方便的算法求解(虽然我对这个算法的表述有一点点疑惑).
除了投影之外, 作者还给出了一个最速下降方向, 证明是类似的.
作者关于\(\ell\)攻击的分析感觉很通透, 不错的文章啊.