[NOI2001]炮兵阵地

洛咕

题意:司令部的将军们打算在N*M的网格地图上部署他们的炮兵部队。一个(N*M)((N<=10,M<=100))的地图由N行M列组成，地图的每一格可能是山地（用“H” 表示），也可能是平原（用“P”表示），如下图.在每一格平原地形上最多可以布置一支炮兵部队(山地上不能够部署炮兵部队);一支炮兵部队在地图上的攻击范围如图中黑色区域所示：

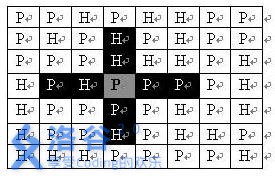
如果在地图中的灰色所标识的平原上部署一支炮兵部队，则图中的黑色的网格表示它能够攻击到的区域：沿横向左右各两格，沿纵向上下各两格。图上其它白色网格均攻击不到。从图上可见炮兵的攻击范围不受地形的影响.现在，将军们规划如何部署炮兵部队，在防止误伤的前提下（保证任何两支炮兵部队之间不能互相攻击，即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内），在整个地图区域内最多能够摆放多少我军的炮兵部队.

分析:状压DP一般都是以一行为一个状态,所以首先可以预处理出同一行任意相邻两个1之间的距离大于等于3(即保证不会出现同一行的打自己人情况)的合法状态,存到集合S中.

设(f[i][j][k])表示前i行,第i行状态为S[j],第i-1行状态为S[k]的合法方案数.(因为第i行的状态同时受i-1和i-2两行的影响,所以要开出两维来存状态,方便我们转移)(不能让j,k两维直接存状态,空间会爆,除非你第一维用滚动数组)

设(count(S[j]))表示S[j]这个状态有多少位是1,(check(i,S[j]))表示S[j]这个状态上为1的位对应到第i行是否全都是平原(即保证布置的炮兵位置合法)

如果(check(i,S[j])=1)且(check(i-1,S[k])=1)且(S[j])&(S[k]=0)且(S[j])&(S[l]=0),(f[i][j][k]=max(f[i][j][k],f[i-1][k][l]+count(S[j])))

目标:如果(check(n,S[i])=1)且(check(n-1,S[j])=1)且(S[i])&(S[j]=1),(ans=max(f[n][i][j]))

//#include<bits/stdc++.h>
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
inline int read(){
   int s=0,w=1;char ch=getchar();
   while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
   while(ch>='0'&&ch<='9'){s=s*10+ch-'0';ch=getchar();}
   return s*w;
}
const int N=1050;
int n,m,sum;
int a[105][15],S[N],f[105][405][405];
inline bool check(int x,int y){//状态y在第x行是否合法
    if(!y)return true;
    for(int i=0;i<m;i++)
	if(((y>>i)&1)&&(a[x][m-i]==2))return false;
    return true;
}
inline int count(int x){//计算x这个状态有多少位1
    int num=0;
    for(int i=0;i<=11;i++)
		if((x>>i)&1)num++;
    return num;
}
int main(){
    n=read(),m=read();
    for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++){
	    	char ch;cin>>ch;
	    	if(ch=='P')a[i][j]=1;//平原
	    	else a[i][j]=2;//山丘
		}
//预处理任意相邻两个1之间的距离大于等于3的合法状态
    for(int i=0;i<(1<<m);i++){
		int last=-1,bj=1;
		for(int j=0;j<m;j++){
	    	if((i>>j)&1){
				if(last==-1)last=j;
				else if(j-last<3){bj=0;break;}
				else last=j;
	    	}
		}
		if(bj)S[++sum]=i;
    }
    for(int i=1;i<=n;i++){
		for(int j=1;j<=sum;j++){
	    	if(!check(i,S[j]))continue;
	    	for(int k=1;k<=sum;k++){
				if(!check(i-1,S[k])||(S[j]&S[k]))continue;
				for(int l=1;l<=sum;l++){
		    		if((S[j]&S[l]))continue;
		    		f[i][j][k]=max(f[i][j][k],f[i-1][k][l]+count(S[j]));
				}
	    	}
		}
    }
    int ans=0;
    for(int i=1;i<=sum;i++){
		if(check(n,S[i])==0)continue;
		for(int j=1;j<=sum;j++){
	    	if(check(n-1,S[j])==0||(S[i]&S[j]))continue;
	    	ans=max(ans,f[n][i][j]);
		}
    }
    printf("%d
",ans);
    return 0;
}