总
圆方树 √
Tarjan求强联通分量、点双、边双 √
Tarjan
这是定义
1、有向图G中,以顶点v为起点的弧的数目称为v的出度,记做deg+(v);以顶点v为终点的弧的数目称为v的入度,记做deg-(v)。
2、如果在有向图G中,有一条 (u,v)有向道路,则v称为u可达的,或者说,从u可达v。
3、如果有向图G的任意两个顶点都互相可达,则称图 G是强连通图,如果有向图G存在两顶点u和v使得u不能到v,或者v不能到u,则称图G是强非连通图。
4、如果有向图G不是强连通图,他的子图G2是强连通图,点v属于G2,任意包含v的强连通子图也是G2的子图,则乘G2是有向图G的极大强连通子图,也称强连通分量。
5、什么是强连通?强连通其实就是指图中有两点u,v。使得能够找到有向路径从u到v并且也能够找到有向路径从v到u,则称u,v是强连通的。
然后我们来看看。
1就是介绍出度与入度,简单来说一个点被连的边数叫入度,一个点连出去的边叫出度。
2废话
3很好懂,只是注意一下是有向图,而且强联通图中任意两点互相到达。
4就是大的图中的强联通块,分成一小块块的强联通图叫强联通分量。
5有向图中,两个点可以互相到达。
看看图,来理解理解:
入度出度:
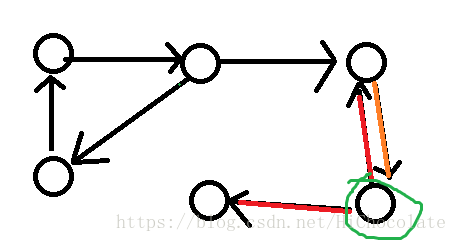
红色是出度,橘色是入度
强联通分量:
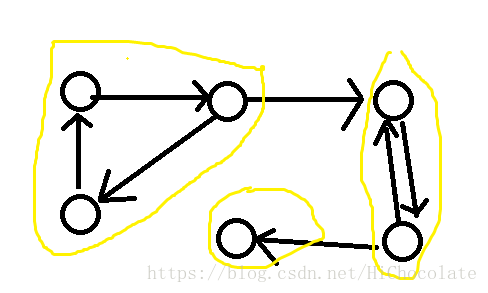
你仔细看这个图不强联通,那么怎么办?
强联通图&点的强联通:
现在懂定义啦,我们就来看看怎么来找出所有的强联通分量。(最简单的问题)
方法一:直接暴力dfs(深搜)求解。
好像没有什么问题,感觉上去是可行的?
真的可行吗?
没错!真的可行,只是它与Tarjan之间有一念之差。
一念之间天堂地狱
方法二:也就是Tarjan=暴力加优化
Tarjan之所以用dfs就是因为它将每一个强连通分量作为搜索树上的一个子树。而这个图,就是一个完整的搜索树。
为了使这颗搜索树在遇到强连通分量的节点的时候能顺利进行。每个点都有两个参数。
首先是dfn[]
DFN[]作为这个点搜索的次序编号(时间戳),简单来说就是 第几个被搜索到的。%每个点的时间戳都不一样%。
2,LOW[]
Q干什么用的呢?
A作为这个点搜索的次序编号(时间戳),简单来说就是用来标记当前节点在深搜过程中是第几个遍历到的点。每个点的时间戳都不一样。
看看图:
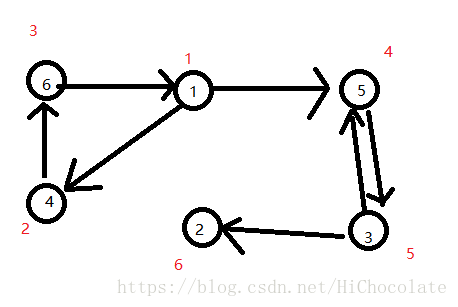
红色字体即为dfn
(当然,这只是一种情况)
然后我们再引入low[]
我们定义它为:作为每个点在这颗树中的,最小的子树的根,每次保证最小。
如果它自己的low[]最小,那这个点就应该从新分配,变成这个强连通分量子树的根节点。
可以得到:low[i]:=min(low[i],low[tov[i]])
(tov[i]指i连到的点)
然后呢,我们每次dfs时,都会产生一个
然后每次找到新的点new,那么这两个东东的值就为dfn[new]=low[new]=now;
然后在回溯的时候就更新low:
low[i]:=min(low[i],low[new]);
这样一来这两个数组就处理好了。
当然,在有向图中要考虑横插边的影响。那么每次就是在一个栈里面搞搞就好。
横插边:
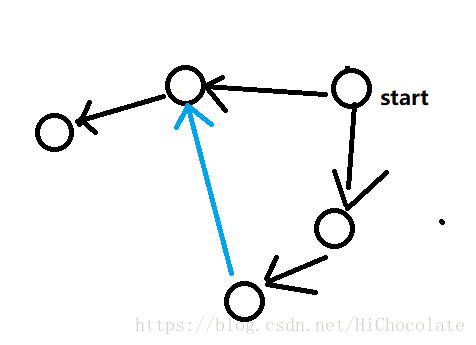
而双向边没有。这个自己想想。
有什么用?你仔细看看,当low[st]=dfn[st]时,就代表有一个新的强联通分量。
很难证明。
于是乎自己手玩感性证明证明。
然后强联通分量就解决了。
我们再来看看如何求点双边双。
以下是无向图
定义:
边双:
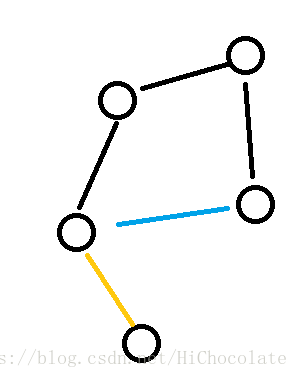
边双指边双连通分量。定义:一个图中没有桥。
假如不看黄边,图中蓝边删掉后,上面的图依然为连通图,那么上面的图为边双。
但是加上黄边,黄边为桥,则图不为边双。
点双:
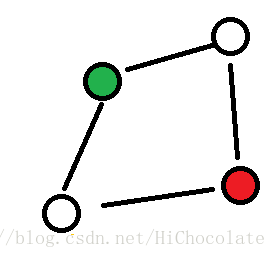
点双指点双联通分量。定义:一个图中任意两个点有至少两条边可以互相到达。
如图中的红点绿点。
这两个东东有什么用?:
——BY Cold_Chair
第一种:
缩边双连通分量。
无向图的边双联通分量其实类似于有向图的强联通分量。
要标记一下走过来的边是哪条,不能直接走回去。
代码:
void tar(int x, int la) {
d[++ d[0]] = x; low[x] = dfn[x] = ++ td;
for(int i = final[x]; i; i = next[i]) if(i != (la ^ 1)){
int y = to[i];
if(!dfn[y]) tar(y, i), low[x] = min(low[x], low[y]); else
low[x] = min(low[x], dfn[y]);
}
if(dfn[x] == low[x]) {
tz ++;
do to[d[d[0]]] = tz; while(d[d[0] --] != x);
}
}第二种:
这种的作用是把仙人掌图搞成缩环树。
仙人掌图标志:任意一条边最多存在与一个简单环中
大概是dfs一下,把环上点的父亲设为环顶(第一次进入环的位置),环顶也可以视作在一个环上,它的父亲设为那个环顶的父亲。
这样缩了以后,处理一些信息(例如最短路)一般只用在lca处特判一下从哪边绕过去。
还是先求出low和dfn。
在仙人掌图中,一个点x,y是x的一个子节点。
如果low[y]>=dfn[x],则说明y上不去,则y的子图就被x隔开了,可以视x为环顶,fa[y]=x.
不然的话y上得去,fa[y] = fa[x]。
找桥点的话则不同,x只要有一个子节点y满足low[y]>=dfn[x],x就是一个桥点。
代码:
void tar(int x, int la) {
low[x] = dfn[x] = ++ td;
for(int i = final[x]; i; i = next[i]) if(i != (la ^ 1)){
int y = to[i];
if(!dfn[y]) tar(y, i), low[x] = min(low[x], low[y]); else
low[x] = min(low[x], dfn[y]);
}
}
void tq(int x) {
bz[x] = 1;
for(int i = final[x]; i; i = next[i]) {
int y = to[i]; if(bz[y]) continue;
if(low[y] >= dfn[x]) fa[y] = x; else fa[y] = fa[x];
tq(y);
}
bz[x] = 0;
}第三种:
这个用来缩点双连通分量。
我们知道割点会存在于多个点双连通分量,所以缩点的话要新开点,并且退栈不要退了当前的点。
用于建圆方树。
Code:
void tar(int x, int la) {
dfn[x] = low[x] = ++ tt;
z[++ z[0]] = x;
for(int i = e.final[x]; i; i = e.next[i]) {
int y = e.to[i];
if(!dfn[y]) {
tar(y, i);
low[x] = min(low[x], low[y]);
if(low[y] >= dfn[x]) {
td ++;
while(z[z[0]] != y) e2.link(z[z[0] --], td);
e2.link(z[z[0] --], td); e2.link(x, td);
}
} else if(i != (la ^ 1)) low[x] = min(low[x], dfn[y]);
}
}圆方树
讲完Tarjan,当然赶紧成热打铁,看看圆方树。
前置技能:
双联通分量:点双
处理对象:
仙人掌树。
这是什么东东?看看一张网上经典图片变成的很有趣的一张图:
额,just for fun。
其实就是一句话:
这个仙人掌中,每条边最多在一个环上。
如何最朴素地处理仙人掌树?
那就用最朴素的dfs。
然后你就会发现,对于一些环,你在dfs之后,会有多出一条返祖边。
由于每条边只会出现在一个环中,所以每一条返祖边覆盖了树中的一条链。
那么显然这条链和这条返祖边构成了环。
于是我们可以确定任何一条边出现在了哪个环中。
你问我这有什么用?
我也不会
其实是可以解决一些关于仙人掌上最大独立集的问题的。
什么是独立集?
独立集是指图 G 中两两互不相邻的顶点构成的集合。任意有关图中团的性质都能很自然的转述成独立集的性质。一般而言,寻找图的最大团是 NP 困难的,从而寻找图的最大独立集也是 NP 困难的。但是,对于二部图的情形,有多项式时间算法找出图的最大独立集。
看不懂?自己去看看“没有上司的舞会”这道题,这道题是树上的最大独立集问题。
这题怎么做呢?我们用树上dp来搞,设f[i,0/1]表示第i个点的儿子选/不选。
很简单对吧?
好吧,扯远了。
圆方树到底是个啥东东?
我们先从字面意义看。
一颗树有圆的节点和方的节点。
屁话
那么,定义是什么?
我们定义原仙人掌上的点为圆点,现在我们考虑转化。
我们对仙人掌进行点双的 Tarjan 算法,因为仙人掌上每个环都是一个点双,而且在栈中的顺序就是环上点的顺序。那么考虑一个点 i 的一条出边(i,j)满足 dfn(i)< low(j),那么说明 (i,j) 是一条树边,我们在 TG 中直接连上这两个点即可;如果 dfn(i)=low(j),那么我们找到了一个环(可能是重边造成的二元环),则从栈中取出点直到取出 j为止,设这样从栈中取出的点集为 R,则 R∪{i}是一个环;对于其他情况,我们按照 Tarjan 的步骤执行即可,无需特殊处理。
看不懂?我们来画图。
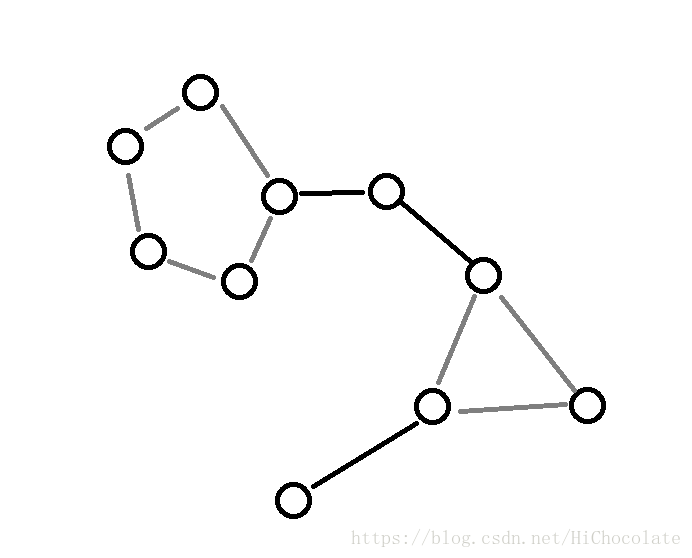
首先,每个原图上的点为圆点。
我们发现,这张图灰色边连成环,那么圆方树是怎么构造的呢?
我们在每个环里面弄一个方点。如下图:
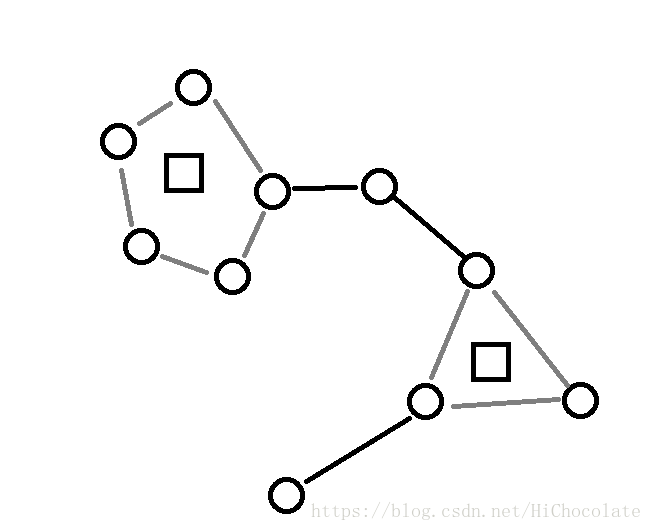
删掉灰边,把环中的点与方点连一条边。
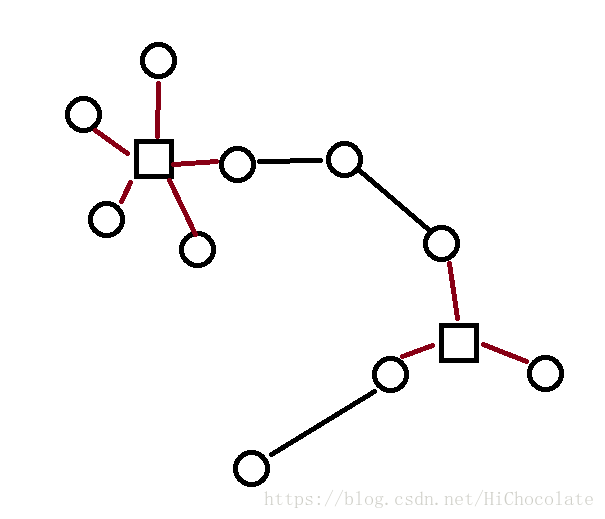
于是,圆方树就构造好了。
具体构造方法:
首先对于原图跑一遍Tarjan。然后求出所有的点双。然后对于每一个点双加入一个方点,把方点与点双中的点连一条边,然后就可以得到圆方树。
如何证明这是一棵树?
由于仙人掌中的所有环都被弄掉了,那不显然是一棵树?
那么我们来看看圆方树的一些性质:
1、每个方点不会与其他方点直接连线。
证明:显然。
2、以任何的一个圆点为根不会影响数的形态。
证明:显然。
3、圆方树是无根树。
证明:不显然吗?
因为以各个点为根,那么只有方点的编号变化,不影响别的点或环。
4、我们先来看看一个定义:
定义:子仙人掌
以r为根的仙人掌上的点p的子仙人掌是去除掉p到r的所有简单路径后,p所在的联通块
很好理解。
那么我们再来看看性质:
当以r为根的仙人掌上,p为子仙人掌,那么在圆方树上,当以人为根,p的子树就相当于p的子仙人掌。
证明:显然?
分类讨论:
1)当p不在r的环上,显然。
2)当p在r的环上。删掉简单路径之后,只有不与p在同一个环内的圆点了,不就是圆方树?
其实很显然。
解决实际问题?
那么我们就来看看:
T1:仙人掌图上的最大独立集问题。
这个我们就来看看圆方树怎么做。
其实也是利用原本的最大独立集问题的思想——dfs+dp。
其实这题根本用不着圆方树,但是你不觉得挂上一个圆方树的牌子很高大上?
进入正题:
对于原本的仙人掌树,我们做一边Tarjan。
然后建出一颗圆方树,然后我们就直接选择一个点为根,做dp。
对于没有与方点连边的点,我们可以直接dp。
但是对于与方点连边的点呢?
我们在这个方点的地方再做一遍dp。
怎么做?
我们看看图:
那么我们依次从最顶上的点,dp下来,很好想+很好打。
其实,不需要用圆方树。
嘿嘿,我们直接在边做Tarjan时边dp即可。当遇到环时就不dp,知道回到最顶上的点,那个时候就可以再反过来搞,做法几乎一样。
T2:【NOIP2017提高A组模拟8.16】最短路
一个仙人掌树,n个点,然后q次询问两个点之间最短路。
n,q<=10^5,
你对spfa够信任吗?
首当其冲的圆方树。
然后,我们就再想想,最短路,树,最短路,树……
不就是lca吗?
那么我们就求一下点到根的最短路,每次询问就跳lca。
但是对于一个环怎么办?
我们再看看上面的图。
我们发现,顶上的点中间切一条路下来,那么就分成了左边和右边,那么,我们就可以把这两边的各个点的最短到根的路给求出来。
那么这个环的问题我们就解决了。
但是还有种情况。
当lca在环上时呢?
我们根据圆方树,我们可以快速求出lca在的环上以及两个点在环上的交点,那么我们同样地去搞,只是在lca 的地方再特判一下即可。
很好搞吧?
T3:【NOI2013模拟】坑带的树
题意:给你一个仙人掌树,有原来的编号,然后给树再编号,使得原来的编号的点连接的别的编号的点在新的编号的树里面同样可以出现,不会出现多出一个点或少了一个点。求方案。
这个解释很垃圾。
也就是:给出一个仙人掌树,问有多少点的映射是的新的树和原来的树同构。
好难的样子。
我们就别想那么难,我们先简化问题,简化成一个树,问有多少点的映射是的新的树和原来的树同构。
这个问题似乎简单些,我们可以用dp来搞搞。
我们由于是要判断重构,那么我们对于一个子树与原树重构,我们可以考虑hash来做,但是可能正确率不能充分保证,于是我们可能需要双hash来搞。
然后有这个条件之后,我们来看看dp怎么搞:
对于一个点,他所有的孩子构成的子树中,记SameTree[Tree]表示形状为Tree的数目,TotalWay[Tree]表示Tree的同构数目,那么这个点,他的同构方案数目就是
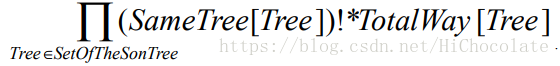
这样我们就可以解决这个问题了。
我们同样地进行构建圆方树。
那么对于普通的点我们可以进行dp。
但是对于环呢?
一个显然的做法:
我们在环上再转一圈来进行更新dp即可。
(小细节很多,所以我没码)
拓展——
一个全新的东东:广义圆方树。
是什么呢?其实也是圆方树,把环变成一个方点连接。
但与原来的圆方树有以下不同:
名字不同
用在的图不同。
原来的圆方树只能用在仙人掌上面,然后变成解决仙人掌问题的利器。
而广义圆方树则可以用于图上面。
做法依然是把图上的环,统统拿出来,用一个方点连接。(一样的)
当然,在原来的基础上建好树后,再把两个圆点有连边的之间,强制加入一个方点。
然后,这就变成圆点与方点是两两相交的。
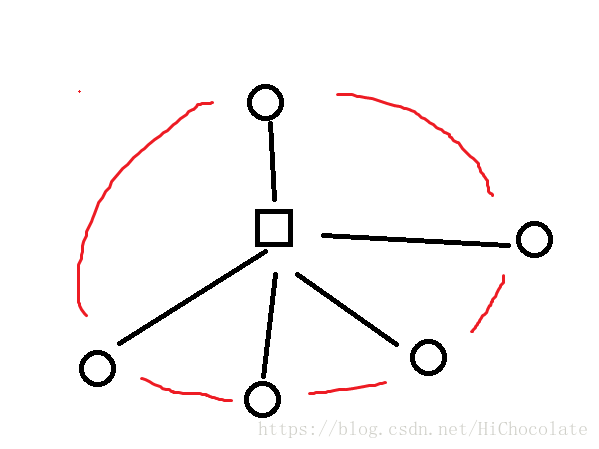
这里网上有一张图:请君看看——
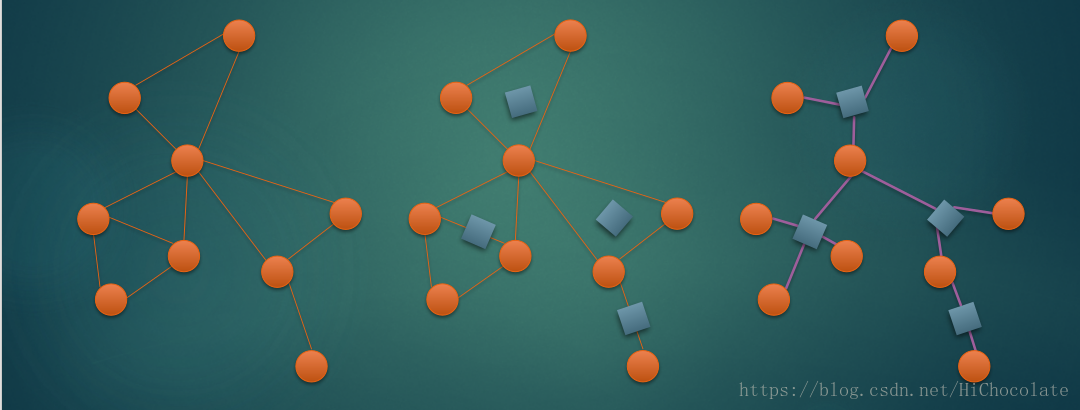
很好理解吧?
这个具体也是用到tarjan来寻找强联通分量,然后再来建树。
于是乎,这就很好地去解决很多题目啦~
T4:【GDOI2015模拟12.21】鸡腿の出行
题意:给你一个图,然后每次询问第i条边到第j条边之间必须经过的点有几个。
稍微有点绕。
建上一颗广义圆方树。
然后呢,我们就发现,可以分类讨论。
如果两条边都没有在强联通分量里面,那么就可以直接lca来走,然后途径的点稍微判断一下即可。
如果有一条边在强联通分量里面,那么我们就直接从对应的方点开始lca,就好了。
如果有两条边的话,同理。
这题好像很简单。
T5:【GDOI2017模拟8.12】旅行
题意:有一个图,然后每个点有一个价值,有很多次询问,每次询问有下面两种:
C a w :表示a号点的价值变为w
A a b :表示询问所有a为起点,b为终点的路径中途径点的最低价值
这题表面上好像很好做,实际上也很好做。
(除非出题人坑你)
一个伏笔
那么我们不看修改,很明显直接套一个树链剖分。
然后呢,我们看看如何处理方点。由于方点是一个强联通分量的中心点,于是方点直接记录这个强联通分量的最小价值即可。
然后跳lca,欧了。
那么我们看看修改,我们可以在修改圆点的同时,顺便修改一下旁边的方点。
这个可以用C++的multiset。
然而对于我这个蛋疼的pascal选手,可以打打线段树,当然,你大佬也可以打斐波那契堆。
于是,就这样解决了。
解决了?
如果这是一个菊花图,那么我们将会相对应地疯狂修改我们的点旁边的所有方点,于是乎,复杂度不就炸了吗?
于是,我们考虑一下,由于广义圆方树的方点与圆点之间交错出现,那么我们就可以用这个性质来做。
我们的方点可以不记录自己的父亲,那么就可以很好地解决这个菊花图的问题。
当然,我们这样子做要注意——如果lca为方点,那么就特判一下lca的父亲。
那么就解决了。
时间复杂度(q*n^2)