[Leetcode]-- Largest Rectangle in Histogram

参考 http://fisherlei.blogspot.com/2012/12/leetcode-largest-rectangle-in-histogram.html

以下摘自水中的鱼：

这样的话，就可以通过大数据。但是这个优化只是比较有效的剪枝，算法仍然是O(n*n).
想了半天，也想不出来O(n)的解法，于是上网google了一下。
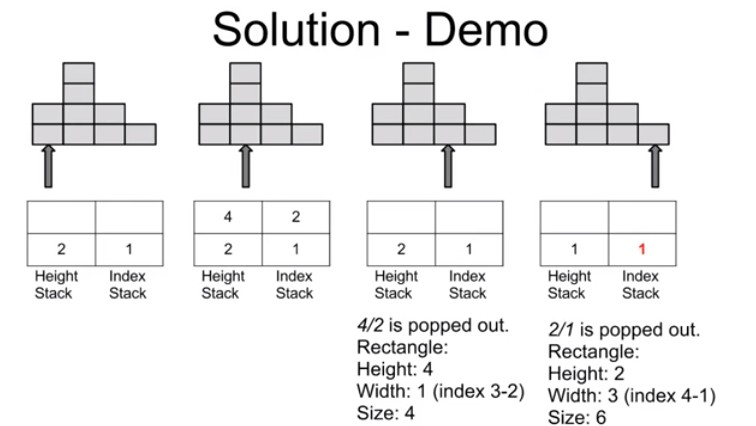
如下图所示，从左到右处理直方，i=4时，小于当前栈顶（及直方3），于是在统计完区间[2,3]的最大值以后，消除掉阴影部分，然后把红线部分作为一个大直方插入。因为，无论后面还是前面的直方，都不可能得到比目前栈顶元素更高的高度了。

这就意味着，可以维护一个递增的栈，每次比较栈顶与当前元素。如果当前元素小于栈顶元素，则入站，否则合并现有栈，直至栈顶元素小于当前元素。结尾入站元素0，重复合并一次。

下面介绍使用两个栈的优化解法。时间复杂度为O(n).

此解法的核心思想为：一次性计算连续递增的区间的最大面积，并且考虑完成这个区间之后，考虑其前、后区间的时候，不会受到任何影响。也就是这个连续递增区间的最小高度大于等于其前、后区间。

这个方法非常巧妙，最好通过一个图来理解：

假设输入直方图为：int[] height = {2,7,5,6,4}.

这个方法运行的时候，当遇到height[2] == 5的时候，发现其比之前一个高度小，则从当前值（5）开始，向左搜索比当前值小的值。当搜索到最左边（2）时，比5小，此时计算在height[0]和height[2]之间的最大面积，注意不包括height[0]和和height[2]。height[1]以红色标出的这个区域就被计算完成。同样的方法，计算出绿色和粉色的面积。

因此这个方法需要使用两个栈。第一个栈为高度栈heightStack，用于记录还没有被计算过的连续递增的序列的值。第二个栈为下标栈indexStack，用于记录高度栈中对应的每一个高度的下标，以计算宽度。

算法具体执行的步骤为：

若heightStack为空或者当前高度大于heightStack栈顶，则当前高度和当前下标分别入站。所以heightStack记录了一个连续递增的序列。

若当前高度小于heightStack栈顶，heightStack和indexStack出栈，直到当前高度大于等于heightStack栈顶。出栈时，同时计算区间所形成的最大面积。注意计算完之后，当前值入栈的时候，其对应的下标应该为最后一个从indexStack出栈的下标。比如height[2]入栈时，其对应下标入栈应该为1，而不是其本身的下标

Using two stack

// O(n) using two stacks
  public int largestRectangleArea(int[] height) {
    // Start typing your Java solution below
    // DO NOT write main() function
    int area = 0;
    Stack<Integer> heightStack = new Stack<Integer>();
    Stack<Integer> indexStack = new Stack<Integer>();
    for (int i = 0; i < height.length; i++) {
      if (heightStack.empty() || heightStack.peek() <= height[i]) {
        heightStack.push(height[i]);
        indexStack.push(i);
      } else if (heightStack.peek() > height[i]) {// 当 heightStack.peek() == height[i] 时候继续循环
        int j = 0;
        while (!heightStack.empty() && heightStack.peek() > height[i]) {
          j = indexStack.pop();
          int currArea = (i - j) * heightStack.pop();
          if (currArea > area) {
            area = currArea;
          }
        }
        heightStack.push(height[i]);
        indexStack.push(j);
      }
    }
    while (!heightStack.empty()) {
      int currArea = (height.length - indexStack.pop()) * heightStack.pop();
      if (currArea > area) {
        area = currArea;
      }
    }
    return area;
  }

思路很巧妙。代码实现如下, 大数据 76ms过。

public class Solution {
     // O(n) using one stack
  public int largestRectangleArea(int[] height) {
    // Start typing your Java solution below
    // DO NOT write main() function
    int area = 0;
    java.util.Stack<Integer> stack = new java.util.Stack<Integer>();
    for (int i = 0; i < height.length; i++) {
      if (stack.empty() || height[stack.peek()] < height[i]) {
        stack.push(i);
      } else {
        int start = stack.pop();
        int width = stack.empty() ? i : i - stack.peek() - 1;
        area = Math.max(area, height[start] * width);
        i--;
      }
    }
    while (!stack.empty()) {
      int start = stack.pop();
      int width = stack.empty() ? height.length : height.length - stack.peek() - 1;
      area = Math.max(area, height[start] * width);      
    }
    return area;
  }

}

  参考：http://blog.csdn.net/abcbc/article/details/8943485