这个plotTree函数,比较聪明,比较简化,比较抽象,作者一定是逐步优化和简化到这个程度的。我是花了小两天时间,断断续续看明白的,还是在参考了另一篇文章以后。这里是链接http://www.cnblogs.com/fantasy01/p/4595902.html。现在尝试讲明白。
总体思想是,找出来需要画图形的坐标,用函数画图。图形一共有三类,一类是父节点,一类是线条,一类是叶子结点。其中“画图”这个动作不难,用matplotlib中的画图功能,非常简单。难的是计算坐标。就像那个著名的斯坦门茨的故事,画线1美元,知道在哪里画线,9999美元。在这里,matplotlib中的函数就是那粉笔,而我们要知道的是在哪里画线。
这里作者有个大前提,就是“居中”,所有的计算都是围绕着这个前提来进行的。每一步计算都是为了居中于节点的所有叶子节点,比如某个节点A有6个叶结点,那么这个节点A就位于这6个节点的正中间。
下面这个函数容易理解,在指定坐标处添加文本。如果父节点坐标已知,子节点坐标已知,找到中间的位置不难。
#在父子节点间填充文本信息 def plotMidText(cntrPt, parentPt, txtString): #书上原式是这样写的,但是计算之后其实就是求中点的公式(parentPt[0] + cntrPt[0]) / 2.0
#书上体现的是中点所在坐标的真正意义,用原点远端点的x坐标减掉近端点的x坐标,得到差值,除以2,就是中点距离两点的绝对距离,再加上近端点的x坐标,就是中点距离原点的距离,
#即中点的x坐标
#y坐标同理
#xMid = (parentPt[0] - cntrPt[0]) / 2.0 + cntrPt[0] xMid = (parentPt[0] + cntrPt[0]) / 2.0 #yMid = (parentPt[1] - cntrPt[1]) / 2.0 + cntrPt[1] yMid = (parentPt[1] + cntrPt[1]) / 2.0 #在(xMid,yMid)坐标处增加文本 createPlot.ax1.text(xMid, yMid, txtString)
下面就是比较难理解的plotTree部分
def plotTree(myTree, parentPt, nodeTxt): numLeafs = getNumLeafs(myTree) #递归取叶结点数 depth = getTreeDepth(myTree) #递归取树的深度(层数) print("叶子数:", numLeafs) print("层数:", depth) print("xOff:", plotTree.xOff) #这一步的结果是一个坐标,(0.5,1.0),子节点的所在位置,为什么要这样计算? #这一步跳过了中间的很多步骤,此式是大量过程化简的结果 cntrPt = (plotTree.xOff + (1.0 + float(numLeafs)) / 2.0 / plotTree.totalW, plotTree.yOff) print("cntrPt",cntrPt) #在父节点和子节点确定之后,在父子之间做文本标记,即nodeTxt
#第一层节点的父坐标与节点坐标相同,其实画了一个长度为0的线,nodeText是空,如果想试验,可以在下面的createTree函数里设置
#plotTree(inTree, parentPt, '中华人民共和国中华人民共和国')
#它就原形毕露了 plotMidText(cntrPt, parentPt, nodeTxt) firstStr = list(myTree.keys())[0] #每层树的首节点名称 plotNode(firstStr , cntrPt, parentPt, decisionNode) #plotNode(firstStr + "[" + str(round(cntrPt[0],2)) + "," + str(round(cntrPt[1],2)) + "]", cntrPt, parentPt, decisionNode) secondDict = myTree[firstStr] plotTree.yOff = plotTree.yOff - 1.0 / plotTree.totalD for key in secondDict.keys(): print("secondDict.keys()中的key:", list(secondDict.keys())[key]) if (type(secondDict[key])).__name__ == 'dict': #字典的值是也是字典(树),继续递归 plotTree(secondDict[key], cntrPt, str(key)) else: #如果字典的值不是字典(是叶子),则直接输出叶子 # plotTree.xOff = plotTree.xOff + 1.0/plotTree.totalW #plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode) a = (plotTree.xOff, plotTree.yOff) plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode) plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key)) plotTree.yOff = plotTree.yOff + 1.0/plotTree.totalD
下面是主程序
def createPlot(inTree): fig = plt.figure(1, facecolor = 'white') #这句可以不写,如果不写,会默认创建一个 #fig = plt.figure(1, facecolor = 'red') #此句会激活1号figure,facecolor白色 #fig = plt.figure(2, facecolor = 'red') #此句会重新创建一个facecolor为红色的figure fig = clf() #清空图形区(plot区、工作区),可能是clear figure的缩写 axprops = dict(xticks=[], yticks=[]) #此参数表示坐标刻度,[]表示不显示刻度,可以作为参数传入,也可以用plt.xticks([1,3,4])单独设置 createPlot.ax1 = plt.subplot(111, frameon = True)#, **axprops) # **表示此参数是字典参数 #plt.xticks([1,3,4],"a,b") #单独设置刻度 #print(axprops) #================================================================================================ plotTree.totalW = float(getNumLeafs(inTree)) #全局变量plotTree.totalW用于存储树的宽度,叶子数 print("总叶子数(宽度):", plotTree.totalW) plotTree.totalD = float(getTreeDepth(inTree)) #全局变量plotTree.totalD用于存储树的深度 print("总层数:", plotTree.totalD) #追踪已经绘制的节点位置,x轴上的偏移量。这只是用于方便计算的一个偏移量,没有实际意义,设置这样一个值以后,后面的只需要加上叶节点的个数就可以了。 #如果0.5不太容易理解,(1/2)*(1/plotTree.totalW),也就是把x轴分为plotTree.totalW份后,其中的1份的一半。 plotTree.xOff = -0.5 / plotTree.totalW; #追踪已经绘制的节点位置,y轴上的偏移量 plotTree.yOff = 1.0 parentPt = (0.5,1.0) #顶层节点的坐标 plotTree(inTree, parentPt, '') #plt.axis([0,10,0,10]) plt.show()
下面是sublime中的调用代码
def testCreatePlot(): inTree = retrieveTree(0) createPlot(inTree)
上面代码中,最核心的是坐标的计算过程。图形在一个x轴和y轴的长度各为1的一个坐标系中绘制。首先计算出叶子节点的数量(为什么要计算这个数量?是因为叶节点需要展开,它们所需要的总宽度是最大的),因为x轴的长度是1,所以用1去除以叶节点的数量,得到每个叶节点所需要的长度,如果x轴的总长度是10,那就用10去除以叶节点的数量,总之这步是在求每个叶子在x轴上所需要的长度。求解思路如下(参考上面所提到的文章):
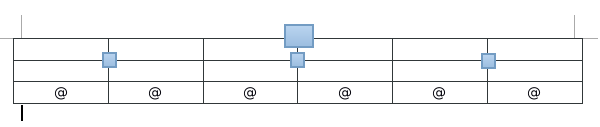
1、其中方形为非叶子节点的位置,@是叶子节点的位置,因此每份(即上图的一个单元格)的长度应该为1/plotTree.totalW,但是叶子节点的位置应该为@所在位置,则在开始的时候plotTree.xOff的赋值为-0.5/plotTree.totalW,即意为开始x位置为第一个表格左边的半个表格距离位置,这样作的好处是:在以后确定@位置时候可以直接加整数倍的1/plotTree.totalW。
这一步一定是经过了作者的逐步优化才得到的。如果不这样做,那么每次取@所在的坐标时,都需要减掉左侧第一个@左边至原点这半个格, 所以作者设置了一个偏移量,以后只需要直接加1个完整的份数,即1/plotTree.totalW,就是下一个叶节点的x坐标,聪明。
2、对于本算法的核心,plotTree函数中的红色部分即如下:
cntrPt = (plotTree.xOff + (1.0 + float(numLeafs))/2.0/plotTree.totalW, plotTree.yOff)
这一步的cntrPt求的是节点所在坐标(x,y)。plotTree.xOff 即为最近绘制的一个叶子节点的x坐标,在确定当前节点位置时每次只需确定当前节点有几个叶子节点,因此其叶子节点所占的总距离就确定了即为float(numLeafs)*(1/plotTree.totalW)(因为总长度为1,如果是总长度是10就用10作分子),比如有4个叶节点,总共有6份,那么所占距离就是4*(1/6),因此当前节点的位置即为其所有叶子节点所占距离的中间,即一半,(float(numLeafs)/2.0)(1/plotTree.totalW),但是由于开始plotTree.xOff赋值并非从0开始,而是左移了半个单元格,因此还需加回来半个单元格距离,即(1/2)(1/plotTree.totalW),计算结果就是(1.0 + float(numLeafs))/2.0/plotTree.totalW*1,因此偏移量确定,则x位置变为plotTree.xOff + (1.0 + float(numLeafs))/2.0/plotTree.totalW。
3、对于plotTree函数参数赋值为(0.5, 1.0)的解释
因为开始的根节点并不用划线,因此父节点和当前节点的位置需要重合,利用2中的确定当前节点的位置便为(0.5, 1.0)
总结:利用这样的逐渐增加x的坐标,以及逐渐降低y的坐标能能够很好的将树的叶子节点数和深度考虑进去,因此图的逻辑比例就很好的确定了,这样不用去关心输出图形的大小,一旦图形发生变化,函数会重新绘制,但是假如利用像素为单位来绘制图形,这样缩放图形就比较有难度了