结对编程作业

结对编程作业报告

各位老师同学们大家好，我们是天地双龙汇小组

GitHub地址

我的GitHub地址：点这里

队友的GitHub地址：点这里

我的博客地址：点这里

队友的博客地址：点这里

具体分工

分类	姓名	具体工作
AI设计	林荣胜	负责完成初期搜索算法C语言向python的转译以及九宫格图像识别和编号
	苏艺淞	负责完成搜索算法的改进和优化以解答题目，完成后续的unittest、样例生成以及性能分析还有博客的算法部分
游戏设计	林荣胜	负责完成ui设计以及博客的原型设计实现部分
	苏艺淞	负责原型设计，测试游戏以及对gui进行改进

orz应测试组要求再整上github代码文件分工，测试组所有代码从我github上拿就好啦

姓名	具体负责文件
苏艺淞	AI文件夹的代码（AI大比拼含算法在内的代码，含主程序AstarFind2.py以及AI大比拼的文件AIFighting.py和AIFightingSimple.py，单元测试代码SampleTest.py以及样例生成代码CreateSample.py）还有就是游戏原型设计的工程文件Klotski.rp（html可以去release看Prototype-design或者直接下载文件夹‘原型设计’）
林荣胜	GUI文件夹的代码（也就是游戏原型设计实现部分）以及release上的GUI-show（游戏展示）以及GUI-game（华容道游戏打包成exe）

原型设计

因为是游戏嘛，又是很传统的华容道游戏，那么就可以偷懒整点花里胡哨的东西了（滑稽摊手.jpg）

这次设计用的是Axure RP，后面听某个大数据张姓靓仔（架在脖子上的刀能放下了吗）说有个叫QtDesigner的东西……果然还是PyQt5学的不够深入（丢人）

QtDesigner：点这里（吐血）

设计说明

我和荣胜讨论如下：首先华容道图片的底板是数字序列（Eg.3x3就是1-9，4x4就是1-16，默认最右下角挖去）然后准备把整个游戏分成三种模式：简单游戏（像小程序那样3x3,4x4,5x5），通关挑战（3x3通关计时制），AI挑战（3x3，计时，比谁步数更接近ai步数）。

原型设计嘛，背景就抽象点啦别太在意= =

点开简单游戏就会有弹窗选择啦

然后就是每个模式的界面啦

简单游戏3x3

简单游戏4x4

简单游戏5x5

通关挑战

AI挑战

排行这边是分成两块，一个是通关排名，还有一个是ai排名

通关排行

AI排行

我们也制定好了详细的游戏规则（见图）:

结对过程

QQ->玫瑰园/益和堂->QQ->玫瑰园/益和堂 周而复始……

遇到的困难及解决方法

其实一开始是用墨刀的，后来还是用了Axure RP，不过还是被整疯了= =（没错我没做之前以为原型设计很简单），所以还是老实去看完网课一个个知识点去查，最后还是把原型给整完了……

更多的问题还是在和荣胜沟通这边把，因为功能是他实现的，我其实一开始的很多设计是和他的思路不太符合的，我没有考虑到用户体验，一些想添加的花边功能还是蛮多余的，开了一次小会协调了一下才有现在的结果

AI与原型设计实现

AI部分

流程图：

算法思路

一开始拿到这题的时候我和荣胜都挺懵逼的，毕竟要用到图像识别的东西。

查了很多关键词为“华容道”的博客，都没有什么太好的头绪，但是我想到图片是固定九宫格切割的，其实我们可以用标号的方式对目标图片的九个部分进行标号，然后题目图片一一对应，转换为另一个问题：给定一个序列，给出每个位置对应可以交换位置上的数的其他位置，目前只能移动一个数字，求尽可能短的操作序列使得题目序列变为目标序列

所以按着这个方向往下查后才发现是经典的八数码问题的变种，当然后来人工智能课也提及到了

核心部分介绍

八数码问题介绍以及七种方式求解这篇博客应该说很完美的为这次结对编程的AI部分提供了方向……七种方法怎么用怎么爽

本着偷懒最高效率的原则我们看完博客后就选择A*算法了，至于什么是A*算法……上面那篇博客已经讲的非常清楚了。

估价函数f(n)就是步数g(n)+每个数字到他目标位置的欧氏距离之和h(n)。

当然传统的A*算法无法解决我们作业的问题，毕竟无解的情况都通过强制交换和自由交换改为有解了，所以我们要对A*算法进行改进：

首先我们要分类讨论一下会遇到的情况：

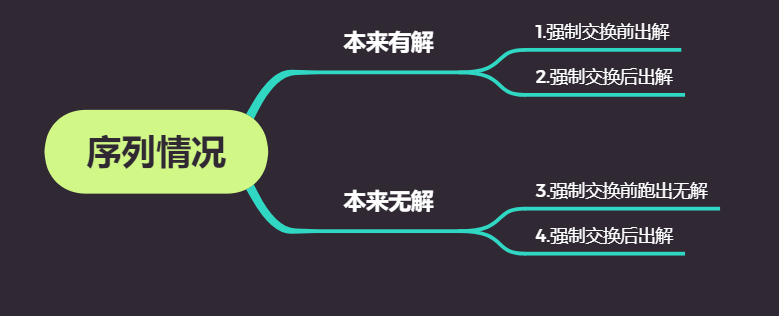
关于如何判定有解可以看这个博客八数码问题判断有解问题及其结论推广（附简要证明）

1的情况就是传统的A*算法就可以处理了，24的情况可以归为一类。

对于24的情况我们在强制交换后如果有解，则继续按A*算法往下跑，若无解，我们需要暴力比对所有位置交换后的估价函数值（当然要在保证是有解的情况下），选择估价函数值最低的交换，然后继续A*算法往下跑。

3的情况比较麻烦一些，目前没有想到更好的方法，只能比较笨的让白块反复横跳到强制交换要求的步数，接着重复24交换的操作。

A*算法里优先队列要用到的结构体如下：

x = [0, 0, 0, 1, 1, 1, 2, 2, 2]
y = [0, 1, 2, 0, 1, 2, 0, 1, 2]
# node类表示当前的局势以及操作序列还有移动步数
# node类表示当前的局势以及操作序列还有移动步数
class node(object):
    def __init__(self, num, step, zeroPos, des, operation, swap, flag):
        # num指当前局势，cost表示用于A*算法的估价函数值，step指移动步数，des指目标状态，operation指操作序列，swap记录自由交换的位置，flag指是否已经被强制交换
        self.num = num
        self.step = step
        self.zeroPos = zeroPos
        self.des = des
        self.Init_zeroPos = self.get_zeroPos()
        self.cost = self.setCost()
        self.operation = operation
        self.swap = swap
        self.flag = flag


   	def __lt__(self, other):
        # 重载运算符，优先队列用得到
        if self.flag == other.flag:
            return self.cost < other.cost
        else:
            return self.flag < other.flag

    def get_zeroPos(self):
        for i in range(9):
            if self.des[i] == 0:
                return i

    def setCost(self):  # A*算法要用到的估价函数
        c = 0
        for i in range(9):
            if self.num[i] != 0:
                c += int((abs(int(i / 3) - x[self.num[i]-1])*abs(int(i / 3) - x[self.num[i]-1]) + abs(int(i%3) - y[self.num[i]-1])*abs(int(i%3) - y[self.num[i]-1]))**0.5)
            else:
                c += int((abs(int(i / 3) - int(self.Init_zeroPos/3))*abs(int(i / 3) - int(self.Init_zeroPos/3)) + abs(int(i%3) - self.Init_zeroPos%3)*abs(int(i%3) - self.Init_zeroPos%3))**0.5)
        return c + self.step


def CostCount(num, des, step):  # 估价函数
    c = 0
    k = 0
    for k in range(9):
        if des[k] == 0:
            break
    for i in range(9):
        if num[i] != 0:
            c += int((abs(int(i / 3) - x[num[i]-1])*abs(int(i / 3) - x[num[i]-1]) + abs(int(i%3) - y[num[i]-1])*abs(int(i%3) - y[num[i]-1]))**0.5)
        else:
            c += int((abs(int(i / 3) - int(k/3))*abs(int(i / 3) - int(k/3)) + abs(int(i%3) - k%3)*abs(int(i%3) - k%3))**0.5)
    return c + step

具体算法代码如下：

# A*算法搜索到达目标局势的最短步数操作
def bfsHash(start, zeroPos, des, step, change_position):
    # 之前采取的是哈希表，由于哈希表会存在冲突问题，然后采取O（n）的后移操作，在面对需要用到大量操作数的时候
    # 算法效率上就会大幅度降低，所以最后用回python自带的字典
    first = node(start, 0, zeroPos, des, [], [], 0)
    que.put(first)
    mymap = {}
    s = ""
    for i in start:
        s += str(i)
    mymap[s] = 1
    m = -1

    # 开始搜索
    while not que.empty():
        tempN = que.get()
        temp = tempN.num.copy()
        pos = tempN.zeroPos

        if check_list(des, temp):  # 若为目标局势则跳出
            return tempN

        if len(tempN.operation) == step and tempN.flag == 0:  # 符合强制交换条件，开始执行变换操作
            # print(2)
            temp = tempN.num.copy()
            if change_position[0] - 1 == pos:
                pos = change_position[1] - 1
            elif change_position[1] - 1 == pos:
                pos = change_position[0] - 1
            temp[change_position[0] - 1], temp[change_position[1] - 1] = temp[change_position[1] - 1], temp[
                change_position[0] - 1]
            swap = []
            if not check(temp, des):
                pos1, pos2 = getRightChange(temp, des, tempN.step)# 获得最优交换
                if pos1 == pos:
                    pos = pos2
                elif pos2 == pos:
                    pos = pos1
                temp[pos1], temp[pos2] = temp[pos2], temp[pos1]
                swap.append(pos1 + 1)
                swap.append(pos2 + 1)
                # print(list)
            s = ""
            for i in temp:
                s += str(i)
            mymap[s] = 1
            operation = tempN.operation.copy()
            temp_step = tempN.step
            tempN = node(temp, temp_step, pos, des, operation, swap, 1)

            if check_list(des, temp):  # 若交换后刚好为目标局势那就直接返回
                # print(des)
                # print(temp)
                # print(tempN.step)
                # print(tempN.operation)
                operation.append(' ')  # 应测试组要求加上一个字符防止评测判断不到交换这一步
                tempN = node(temp, temp_step, pos, des, operation, swap, 1)
                return tempN

        # cnt用来对付无解情况，四个方向（cnt=4）都无路可走就为无解情况。
        # 如果这个情况出现在强制交换要求的步数前那么我们要添加“反复横跳”操作使得他达到强制交换要求的步数
        cnt = 0
        for i in range(4):
            if changeId[pos][i] != -1:
                pos = tempN.zeroPos
                temp = tempN.num.copy()
                temp[pos], temp[changeId[pos][i]] = temp[changeId[pos][i]], temp[pos]
                # print(k)
                s = ""
                for j in temp:
                    s += str(j)
                if s not in mymap:
                    #    print(1)
                    mymap[s] = 1
                    operation = tempN.operation.copy()
                    operation.append(dir[i])
                    temp_step = tempN.step + 1
                    temp_num = temp
                    tempM = node(temp_num, temp_step, changeId[pos][i], des, operation, tempN.swap, tempN.flag)
                    que.put(tempM)
                else:
                    cnt += 1
            else:
                cnt += 1

        if cnt == 4 and tempN.step < step:  # 进行“反复横跳”操作
            # 对于在强制交换前就发现无解的情况，我们直接处理成白块来回摆动的情况让他直接到达目标步数
            temp = tempN.num.copy()
            operation = tempN.operation.copy()
            # print(len(operation))
            m = operation[len(operation) - 1]
            delta = step - len(operation)
            pos = tempN.zeroPos
            temp, operation, pos = getOrder(temp, operation, delta, m, pos)  # 添加“反复横跳”的操作序列
            tempM = node(temp, step, pos, des, operation, tempN.swap, tempN.flag)
            que.put(tempM)

图片处理

那么如何实现图片标号呢，这个时候就要用到我们的cv2库（在opencv-python库内）还有Image库了，有了Image库我们可以轻松实现对一张图的九宫格切割，所以我们先预处理测试组给我们的36张图，把他们都按九宫格的格式切割成九张图，存在cut_chars文件夹里

然后就是在我们的主程序里执行拿图操作和这36个文件夹做对比了，相同图片数为8张就说明是这副图了（其中有一个被挖去做白色块了，这个要标0），顺便把白色块对应的原序列的数标0

代码如下：

# 拿到我们的图以及其他要求信息，与之前预被处理成九宫格的36个正常字符图进行比对并标号
def getProblemImageOrder(stuid):
    # 拿图
    url = 'http://47.102.118.1:8089/api/problem?stuid=' + stuid
    r = requests.get(url)
    dict = r.json()
    target = base64.b64decode(dict['img'])
    file = open('json_img_test.jpg', 'wb')
    file.write(target)
    file.close()

    # 切图
    img = cv2.imread('json_img_test.jpg')
    height = img.shape[0]
    width = img.shape[1]
    single_height = height / 3
    single_width = width / 3
    for i in range(3):
        for j in range(3):
            dst = img[int(i * single_height):int((i + 1) * single_height),
                  int(j * single_width):int((j + 1) * single_width)]
            # img_list.append(dst)
            # 在本目录生成被分割的图片
            cv2.imwrite(str(i * 3 + j) + '.jpg', dst)

    # 开始对号入座
    init_path = 'cut_chars'
    for file in os.listdir(init_path):
        path = init_path + '\' + str(file)
        count = 0
        for img_name in os.listdir(path):
            # print(path + '\' + str(img_name))
            img = cv2.imread(path + '\' + str(img_name))
            for i in range(9):
                temp_path = str(i) + '.jpg'
                temp = cv2.imread(temp_path)
                if (temp == img).all():
                    count = count + 1
                    break
            # print(count)
        if count == 8:
            print(file)
            break

    order = []
    path1 = 'cut_chars' + '\' + str(file) + '\'
    for k in range(9):
        sum = 0
        path2 = str(k) + '.jpg'
        # print(path2)
        img2 = cv2.imread(path2)
        for i in range(1, 4, 1):
            for j in range(1, 4, 1):
                temp = path1 + str(i) + ',' + str(j) + '.jpg'
                # print(temp)
                img1 = cv2.imread(temp)
                if (img1 == img2).all():
                    sum = (i - 1) * 3 + j
        if sum > 0:
            order.append(sum)
        else:
            order.append(0)

    return order, dict['step'], dict['swap'], dict['uuid']


def getDestImageOrder(order):  # 得确定哪块空了，将其标号为0表示白色块
    dst = [1, 2, 3, 4, 5, 6, 7, 8, 9]
    map = {}
    for i in order:
        map[i] = 1
    # print(map)
    for m in range(0, len(dst)):
        if dst[m] not in map.keys():
            dst[m] = 0
            break
    return dst

性能分析与优化

关于防止当前局势重复出现

最早荣胜把博客上的C++代码转成python代码的时候用的是字典来判断当前局势是否重复，但是我觉得哈希表判断应该会更快所以用了哈希表（显然我这个哈希表写的稀烂）。

# 哈希表
def hashfuction(n, N):
    return int(n) % int(N)


class HashTable(object):

    def __init__(self, size):
        self.size = size
        self.Next = [0] * self.size
        self.Hashtable = [0] * self.size

    def tryInsert(self, n, N):
        # print(n)
        hashvalue = hashfuction(n, N)
        while self.Next[hashvalue]:
            if self.Hashtable[hashvalue] == n:
                return False
            hashvalue = self.Next[hashvalue]
        # print(hashvalue)
        if self.Hashtable[hashvalue] == n:
            return False
        j = N - 1
        while self.Hashtable[j]:
            j = j + 1
        self.Next[hashvalue] = j
        self.Hashtable[j] = n
        return True

    def Hashshow(self):
        print(self.Next)
        print(self.Hashtable)

我写的哈希表在面对一些api上的一些题目的时候时间消耗并没有非常大

但是有些就不太一样了orz

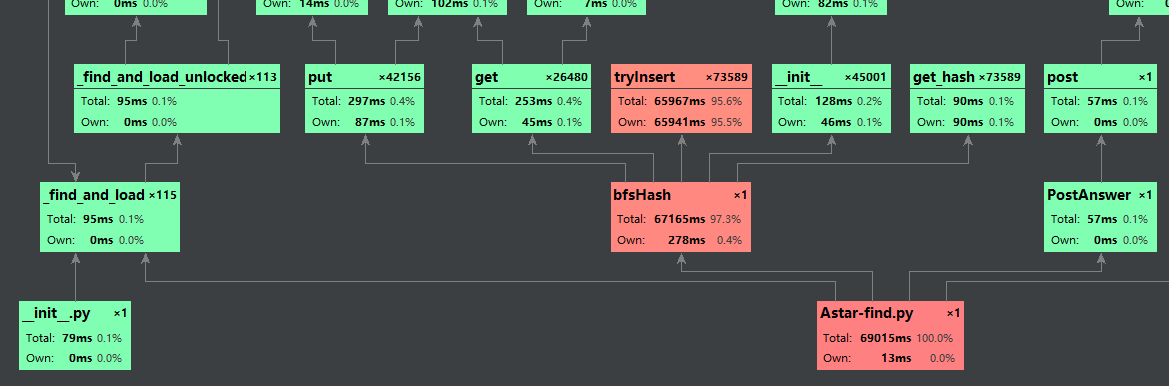
这个tryInsert——哈希表插入直接把我脸打肿了orz，显然如果有太多哈希冲突的话找空位时间会大大提高：

while self.Hashtable[j]:
            j = j + 1
self.Next[hashvalue] = j
self.Hashtable[j] = n

所以老实用回字典了，真的快了好多

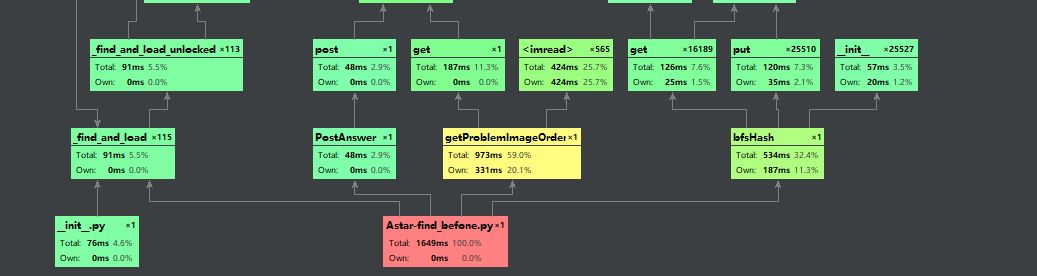
可以看到A*搜索函数的耗时大大降低了

估价函数对比

其实我和荣胜一开始的估价函数f(n)为步数g(n)+“不在位”数字个数h(n)，但是人工智能课刚好有讲到八数码问题，ppt上有提及另外一种估价函数步数g(n)+每个数字到他目标位置的曼哈顿距离之和h(n)，结合书上定理：

有两个A*算法A1和A2，若A2比A1有较多的启发信息（即对所有节点均有h2(n)>h1(n)），则在具有一条从s到t的路径的隐含图上，搜索结束时，由A2所扩展的每一个结点，也必定由A1所扩展，即A1扩展的结点至少和A2一样多

显然后者的启发信息肯定比前者多，所以搜索效率上一定不比前者差，所以我们在单元测试上作了对比：

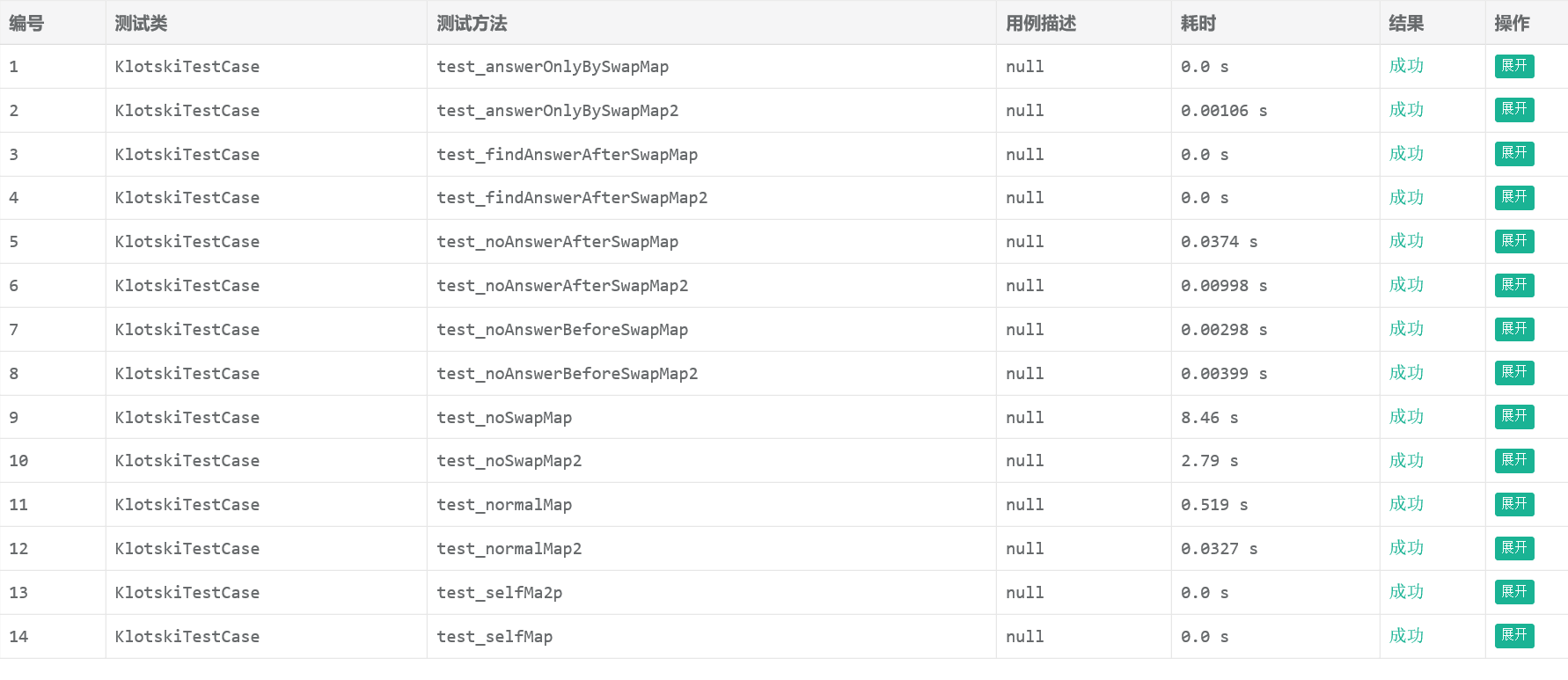
前者的估价函数：

    def setCost(self):  # A*算法要用到的估价函数
        c = 0
        for i in range(9):
            if self.num[i] != self.des[i]:
                c = c + 1
        return c + self.step

后者的估价函数：

    def setCost(self):  # A*算法要用到的估价函数
        c = 0
        for i in range(9):
            if self.num[i] != 0:
                c += abs(int(i / 3) - self.x1[self.num[i]-1]) + abs(int(i%3) - self.y1[self.num[i]-1])
            else:
                c += abs(int(i / 3) - int(self.Init_zeroPos/3)) + abs(int(i%3) - self.Init_zeroPos%3)
        return c + self.step

可见，第二种（也就是我们前面说的后者）速度更快。

2020.10.13更新

然后跑ai大比拼测试的时候我愣是被同学们出的题狠狠的打脸了，因为曼哈顿距离之和不一定最优，反而“不在位”个数能保证部分最优（裂开）

甚至连我自己测的时候都发现了不对劲hhhh

于是我就去百度了新的估价函数，然后就用上了欧氏距离emmmm 两种启发函数解决八数码问题

测评结果如下：

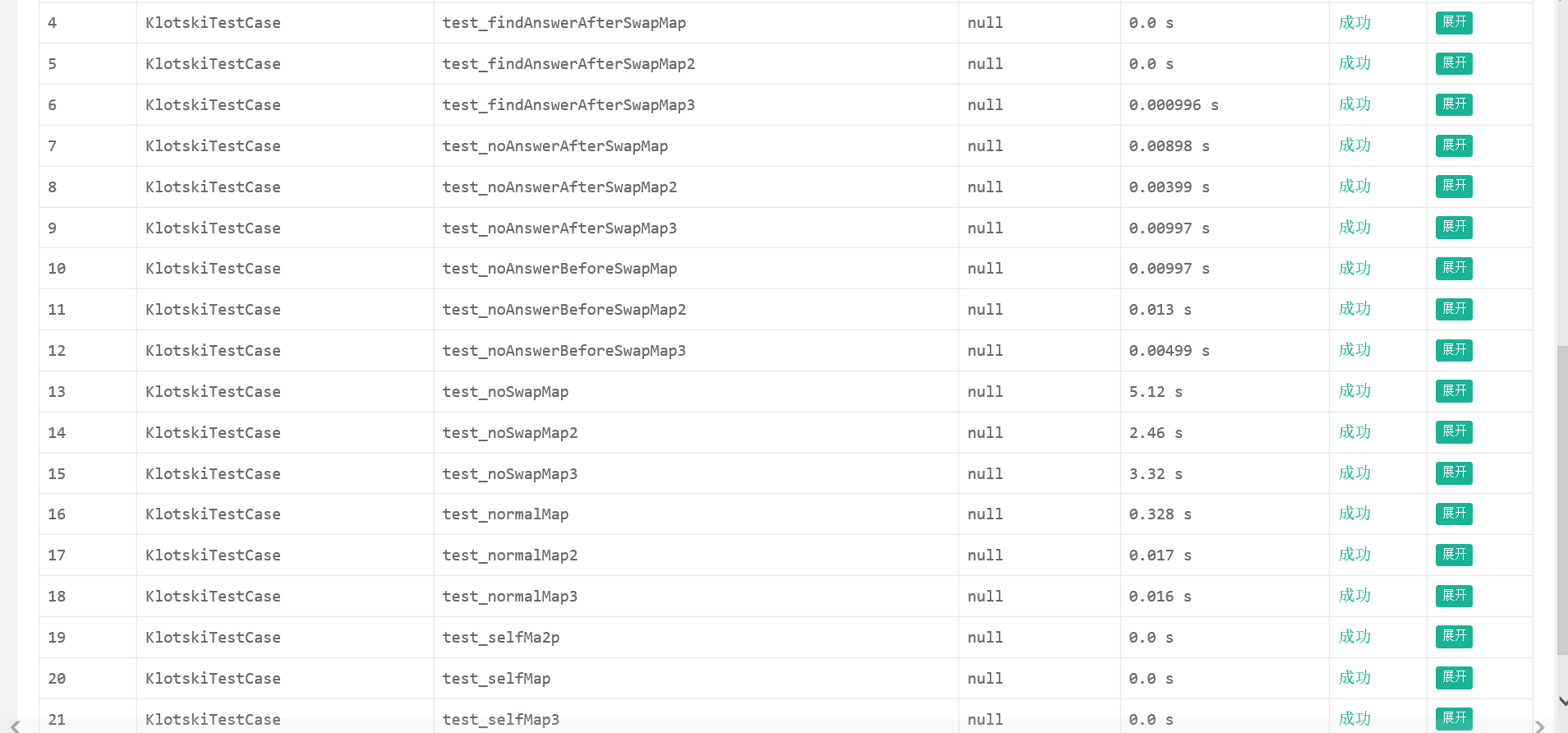
可以看得出来，时间效率上和曼哈顿差不多

和“不在位”个数一样能保证步数上的最优。

当然后面发现我们的问题并不是出现在估价函数上

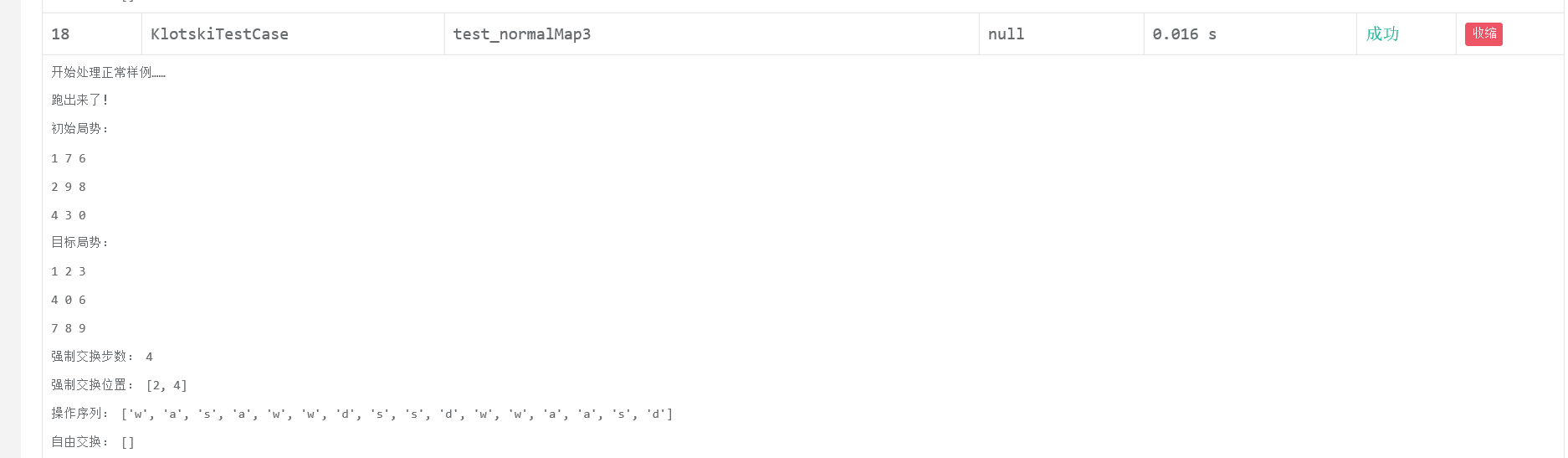
强制交换带来的估价变动

深思了一下为什么曼哈顿距离之和不一定能达到最优的原因后，我想可能是因为交换的瞬间能带来估价函数值的大量减少，考虑极限情况（0,0）和（2，2）对调位置后两个数字都达到正确位置，此时估价函数减8，是有可能达到最小的，然而在我们当前的A*算法中，优先队列可能不会优先扩展这种节点（函数值比较大，队列中位置靠后），可能还没扩展就出“最优解”了（显然此时的解不一定是最优的）。

目前能想到的方法就是把所有未交换的节点都先优先扩展了，对于未交换与未交换之间，已交换与已交换之间，相同状态的节点（）我们还是按估价函数最小的优先扩展。

这样能保证大部分情况有最优解，泪目有的还不是最优：

最终性能分析

单元测试

由于这道题的本质是八数码问题的变种，所以我们生成的样例数据也只是序列，关注的函数是A*搜索函数bfsHash

我们把我们所要的函数提取出来打包成另一个函数（answer和answer2对应性能分析里的两个估价函数，前后关系一致）：

# 用于对付unittest
def showmap(temp):
    for i in range(0, len(temp), 3):
        str1 = str(temp[i]) + ' ' + str(temp[i + 1]) + ' ' + str(temp[i + 2])
        print(str1)


def SampleSolve(order, origin, swap, swapStep):
    # 确定白块位置
    for k in range(9):
        if order[k] == 0:
            break
    # 开始搜索
    b = answer.bfsHash(order, k, origin, swapStep, swap)
    print('跑出来了！')
    print('初始局势：')
    showmap(order)
    print('目标局势：')
    showmap(origin)
    print('强制交换步数：', swapStep)
    print('强制交换位置：', swap)
    print('操作序列：', b.operation)
    print('自由交换：', b.swap)
    return b.operation

def SampleSolve2(order, origin, swap, swapStep):
    # 确定白块位置
    for k in range(9):
        if order[k] == 0:
            break
    # 开始搜索
    b = answer2.bfsHash(order, k, origin, swapStep, swap)
    print('跑出来了！')
    print('初始局势：')
    showmap(order)
    print('目标局势：')
    showmap(origin)
    print('强制交换步数：', swapStep)
    print('强制交换位置：', swap)
    print('操作序列：', b.operation)
    print('自由交换：', b.swap)
    return b.operation

数据构造

对于所有的样例，我们都是以随机挖去数字作白块，先交换后随机白块移动的方式达到每个样例的目标

纵观整个样例测试过程，我们可以总结出以下几个典型样例：

1.正常样例（就是按前面所说的做处理，强制交换步数调整在[0，20]当中的数，因为基本出解在这个区间里）

2.有移动，交换后直接出解的样例

3.没有移动，只有交换就可以出解的样例

4.算法跑出无解的最大步数在强制交换要求的步数前的样例

5.算法跑出无解的最大步数在强制交换要求的步数后的样例

6.在强制交换步数前就能出解的样例

7.原图对比

其中，34567是可以构造的，2目前还不知道怎么造orz，只能拿api上跑出来的特例作代替

对于3：我们只需要将两个相邻的数字作对调，这个时候序列必定无解.此时再对任意两个位置作交换，这两个交换作为强制交换要的位置，强制交换要求的步数设置成0。

对于4和5：同样也是将两个相邻的数字作对调，随机移动若干次，然后用传统的A*搜索跑出判定无解的最大步数后做调整即可

对于6：直接将原图随机移动若干次，用传统的A*算法跑出最优解，将强制交换位置要求的步数放在最优解步数后即可。

代码如下：

def CreateNormalSample():
    # 正常的变种八数码问题随机生成的样例
    # 首先随机挖一块图片作白块
    origin = [1, 2, 3, 4, 5, 6, 7, 8, 9]
    k = random.randint(0, 8)
    origin[k] = 0
    # 随机交换两个块
    order = origin.copy()
    swap = []
    k1 = random.randint(0, 8)
    k2 = random.randint(0, 8)
    swap.append(k1+1)
    swap.append(k2+1)
    if k == k1:
        k = k2
    elif k == k2:
        k = k1
    order[k1], order[k2] = order[k2], order[k1]
    # 随机走500下
    for i in range(500):
        random_num = random.randint(0, 3)
        if changeId[k][random_num] != -1:
            order[k], order[changeId[k][random_num]] = order[changeId[k][random_num]], order[k]
            k = changeId[k][random_num]
    step = random.randint(0, 20)  # 在主程序跑的过程中我们发现基本最大的步数都是在20步左右
    return origin, order, swap, step


def CreateNoSwapSample():  # 存在解在未交换前就跑出来了
    # 正常随机交换后随机移动若干次
    # 首先随机挖一块图片作白块
    origin = [1, 2, 3, 4, 5, 6, 7, 8, 9]
    k = random.randint(0, 8)
    origin[k] = 0
    order = origin.copy()
    # print(origin)
    # 开始随机移动
    for i in range(500):
        random_num = random.randint(0, 3)
        # print(k)
        if changeId[k][random_num] != -1:
            order[k], order[changeId[k][random_num]] = order[changeId[k][random_num]], order[k]
            k = changeId[k][random_num]
            # print(order)
    # print(answer.check(order,origin))
    shortestStep = NormalRun(order, k, origin)
    print(shortestStep)
    swapStep = shortestStep + random.randint(0, 5)
    swap = []
    k1 = random.randint(0, 8)
    k2 = random.randint(0, 8)
    swap.append(k1+1)
    swap.append(k2+1)
    return origin, order, swap, swapStep


def CreateNoAnswerAfterSwapSample():  # 必须在交换后才有解且Astar存在发现无解的情况在强制交换要求的步数后
    # 直接随机选取两个临近位置的块交换便可无解
    # 首先随机挖一块图片作白块
    origin = [1, 2, 3, 4, 5, 6, 7, 8, 9]
    k = random.randint(0, 8)
    origin[k] = 0
    order = origin.copy()
    while answer.check(origin, order):
        k1 = random.randint(0, 8)
        k2 = random.randint(0, 8)
        if k == k1:
            k = k2
        elif k == k2:
            k = k1
        order[k1], order[k2] = order[k2], order[k1]
    limited_swap = NoAnswerRun(order, k, origin)
    swap = []
    k1 = random.randint(0, 8)
    k2 = random.randint(0, 8)
    swap.append(k1+1)
    swap.append(k2+1)
    if limited_swap:
        swapStep = random.randint(1, limited_swap)
    else:
        swapStep = 0
    return origin, order, swap, swapStep


def CreateNoAnswerBeforeSwapSample():  # 必须在交换后才有解且Astar存在发现无解的情况在强制交换要求的步数前
    # 直接随机选取两个临近位置的块交换便可无解
    # 首先随机挖一块图片作白块
    origin = [1, 2, 3, 4, 5, 6, 7, 8, 9]
    k = random.randint(0, 8)
    origin[k] = 0
    order = origin.copy()
    while answer.check(origin, order):
        k1 = random.randint(0, 8)
        k2 = random.randint(0, 8)
        if k == k1:
            k = k2
        elif k == k2:
            k = k1
        order[k1], order[k2] = order[k2], order[k1]
    limit_step = NoAnswerRun(order, k, origin)
    swap = []
    k1 = random.randint(0, 8)
    k2 = random.randint(0, 8)
    swap.append(k1+1)
    swap.append(k2+1)
    swapStep = limit_step + random.randint(1, 10)
    return origin, order, swap, swapStep


def CreateOriginMapCheck():  # 原图对比
    origin = [1, 2, 3, 4, 5, 6, 7, 8, 9]
    k = random.randint(0, 8)
    origin[k] = 0
    order = origin.copy()
    step = random.randint(0, 20)
    swap = []
    k1 = random.randint(0, 8)
    k2 = random.randint(0, 8)
    swap.append(k1+1)
    swap.append(k2+1)
    if k == k1:
        k = k2
    elif k == k2:
        k = k1
    return origin, order, swap, step


def CreateFindAnswerAfterSwapSample():  # 交换后马上找到结果
    # 目前没有想到有效的数据创造方法，先用apiget到的样例
    origin = [1, 0, 3, 4, 5, 6, 7, 8, 9]
    order = [4, 1, 7, 5, 6, 9, 3, 8, 0]
    swap = [6, 6]
    swapStep = 5
    return origin, order, swap, swapStep


def CreateAnswerOnlyBySwapSample():  # 一开始交换完就是目标局势
    origin = [1, 2, 3, 4, 5, 6, 7, 8, 9]
    k = random.randint(0, 8)
    origin[k] = 0
    order = origin.copy()
    k1 = k
    while k == k1 or k == k1 + 1:
        k1 = random.randint(0, 7)
    order[k1], order[k1+1] = order[k1+1], order[k1]
    k1 = random.randint(0, 8)
    k2 = random.randint(0, 8)
    swap = []
    if k == k1:
        k = k2
    elif k == k2:
        k = k1
    order[k1], order[k2] = order[k2], order[k1]
    swap.append(k1+1)
    swap.append(k2+1)
    swapStep = 0
    return origin, order, swap, swapStep

测试代码

一样的也是用unittest，由于要比对两个估价函数，这次我们选择把样例在test类外先提前生成再做测试

origin1, order1, swap1, step1 = sample.CreateNormalSample()
origin2, order2, swap2, step2 = sample.CreateNoSwapSample()
origin3, order3, swap3, step3 = sample.CreateNoAnswerAfterSwapSample()
origin4, order4, swap4, step4 = sample.CreateNoAnswerBeforeSwapSample()
origin5, order5, swap5, step5 = sample.CreateOriginMapCheck()
origin6, order6, swap6, step6 = sample.CreateFindAnswerAfterSwapSample()
origin7, order7, swap7, step7 = sample.CreateAnswerOnlyBySwapSample()

class KlotskiTestCase(unittest.TestCase):

    def test_normalMap(self):
        print("开始处理正常样例……")
        operation = sample.SampleSolve(order1, origin1, swap1, step1)

    def test_noSwapMap(self):
        print("正在处理不需交换的样例……")
        operation = sample.SampleSolve(order2, origin2, swap2, step2)
        if len(operation) > step2:
            raise NoSwapError

    def test_noAnswerAfterSwapMap(self):
        print("正在处理无解判定在交换要求步数后的样例……")
        operation = sample.SampleSolve(order3, origin3, swap3, step3)

    def test_noAnswerBeforeSwapMap(self):
        print("正在处理无解判定在交换要求步数前的样例……")
        operation = sample.SampleSolve(order4, origin4, swap4, step4)

    def test_selfMap(self):
        print("自己和自己比对哦~~~")
        operation = sample.SampleSolve(order5, origin5, swap5, step5)
        if len(operation) > 0:
            raise SameMapError

    def test_findAnswerAfterSwapMap(self):
        print("正在处理交换后得解的样例……")
        operation = sample.SampleSolve(order6, origin6, swap6, step6)
        if len(operation) < step6:
            raise SwapError

    def test_answerOnlyBySwapMap(self):
        print("正在处理只交换就出解的样例……")
        operation = sample.SampleSolve(order7, origin7, swap7, step7)
        if operation[0] != ' ':
            raise MoveError

    def test_normalMap2(self):
        print("开始处理正常样例……")
        operation = sample.SampleSolve2(order1, origin1, swap1, step1)

    def test_noSwapMap2(self):
        print("正在处理不需交换的样例……")
        operation = sample.SampleSolve2(order2, origin2, swap2, step2)
        if len(operation) > step2:
            raise NoSwapError

    def test_noAnswerAfterSwapMap2(self):
        print("正在处理无解判定在交换要求步数后的样例……")
        operation = sample.SampleSolve2(order3, origin3, swap3, step3)

    def test_noAnswerBeforeSwapMap2(self):
        print("正在处理无解判定在交换要求步数前的样例……")
        operation = sample.SampleSolve2(order4, origin4, swap4, step4)

    def test_selfMa2p(self):
        print("自己和自己比对哦~~~")
        operation = sample.SampleSolve2(order5, origin5, swap5, step5)
        if len(operation) > 0:
            raise SameMapError

    def test_findAnswerAfterSwapMap2(self):
        print("正在处理交换后得解的样例……")
        operation = sample.SampleSolve2(order6, origin6, swap6, step6)
        if len(operation) < step6:
            raise SwapError

    def test_answerOnlyBySwapMap2(self):
        print("正在处理只交换就出解的样例……")
        operation = sample.SampleSolve2(order7, origin7, swap7, step7)
        if operation[0] != ' ':
            raise MoveError

然后呢，发现用runner是可以一次性添加多个test的，上次一个个加真的很影响观感自己也写得很累orz

如何一下添加所有测试样例

if __name__ == '__main__':
    #unittest.main()

    tests = unittest.makeSuite(KlotskiTestCase)
    runner = BeautifulReport(tests)  # => tests是通过discover查找并构建的测试套件
    runner.report(
        description='华容道测试报告',  # => 报告描述
        filename='Klotski.html',  # => 生成的报告文件名
        log_path='.'  # => 报告路径
    )

真的是有被舒服到啊！！！

原型设计实现

1）大致介绍

该GUI为一款数字华容道游戏，有三种游戏模式：简单游戏、通关挑战、AI挑战，其中，两种挑战模式将会记录前十次历史最好成绩。另外，该游戏设计了AI演示功能，利用A*算法求解当前局势的最优路径，能够分别以动画演示、逐步演示和步数序列友好地向用户演示。本文将介绍该GUI大致的设计思路和关键技术，该GUI使用PyQt5库实现。

2）游戏设计思路导图

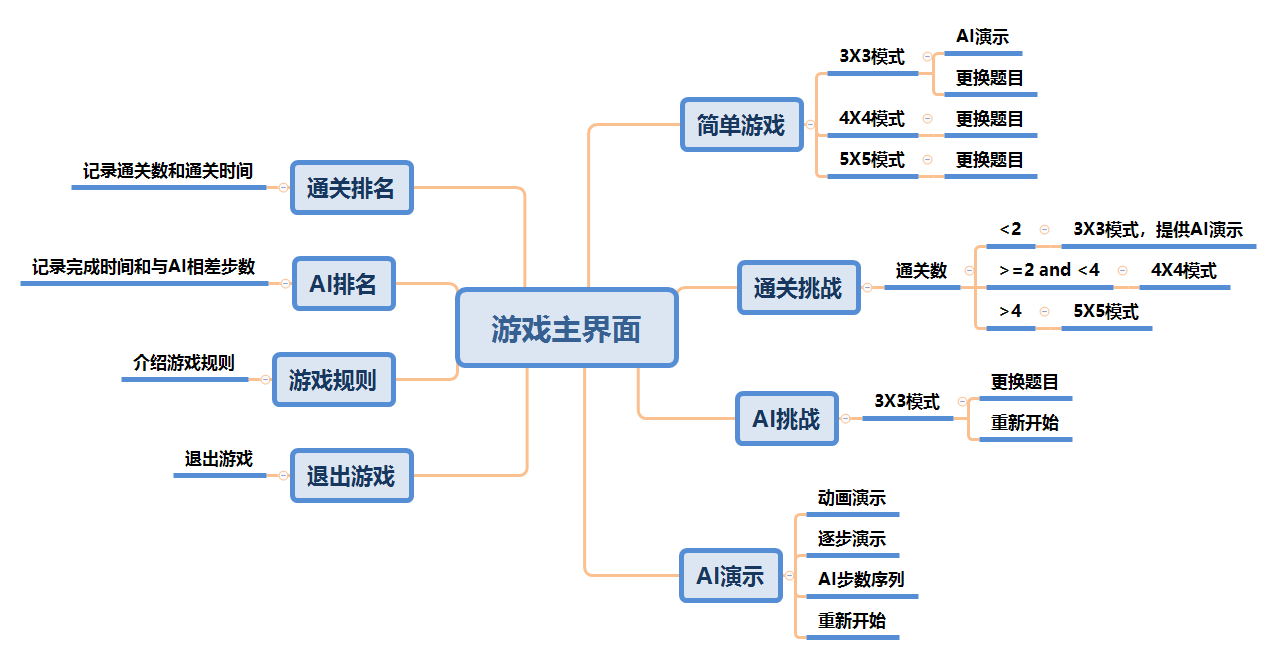
3）GUI分析

游戏主界面

• 为了界面美观，该界面没有使用布局方式，通过手动设置button和“华容道”这三个字的位置，并使用setFixedSize设置禁止对窗口大小进行改变。
• 考虑用户的游戏体验，在点击每个button后，弹出子窗口，应该隐藏父窗口。这时应该在每个button的点击响应函数中，加入self.hide()，隐藏该界面。、

# 实现子窗口弹出，父窗口隐藏
def callRank(self):
	self.rank_window = RankWindow()
	self.hide()
	self.rank_window.show()

简单游戏选择界面

• 点击button选择三个不同简单游戏模式。
• 该界面使用QHBoxLayout布局方式，使三个按钮均匀分布在水平方向。

简单游戏3X3模式

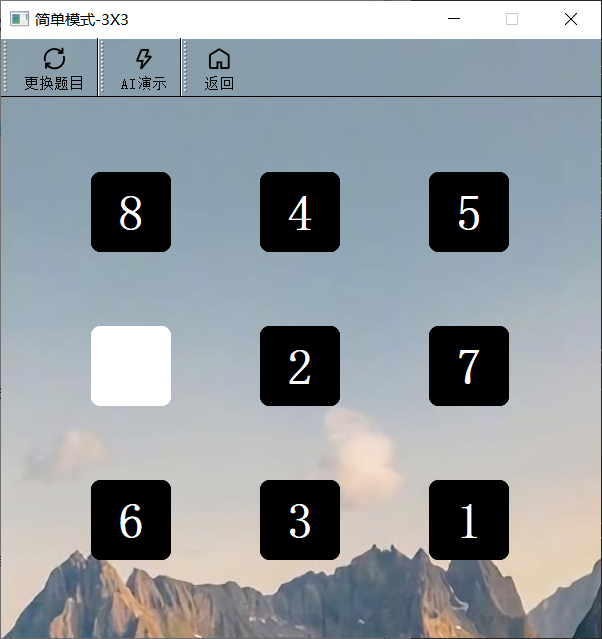
• 数字方块继承QLabel，建立9个数字方块，并将其放入QGridLayout网格布局中。因为该界面继承了QMainWinodw，所以应将QGridLayout放入QWidget，再将QWidget放入QMainWindow的setCentralWidget。
• 要实现移动方块，这里是使用状态数组顺序存入数字方块上的数字编号（这样在实现AI演示时也更加方便），移动时，只要交换白块（数组中设置为0）和移动位在数组中的位置。也就是说，目标状态为[1,2,3,4,5,6,7,8,0]，当然也可以使用二维数组的形式。
• 这里还要监听键盘的上下左右事件，来相应地对数字方块进行移动，在每次移动后都要对QGridLayout进行“刷新”，即重新将9个数字方块放入QGridLayout中。同时，每次移动后，还要对当前状态数组进行判断是否是目标状态，如果完成，弹出消息框祝贺玩家。
• 设置一个更换题目按键，即重新初始化状态数组和白块的位置。
• 设置一个返回按键，即返回到游戏主界面。
• AI演示将在下文统一介绍。

# QMainWindow中一定要的步骤
self.gltMain = QGridLayout()
mainframe = QWidget()
mainframe.setLayout(self.gltMain)
self.setCentralWidget(mainframe)
# 刷新操作，其中Block为数字方块（继承自QLabel），self.blocks为状态二维数组
def updatePanel(self):
    for row in range(3):
        for column in range(3):
            self.gltMain.addWidget(Block(self.blocks[row][column]), row, column)
            self.setLayout(self.gltMain)

简单游戏4X4模式和简单游戏5X5模式

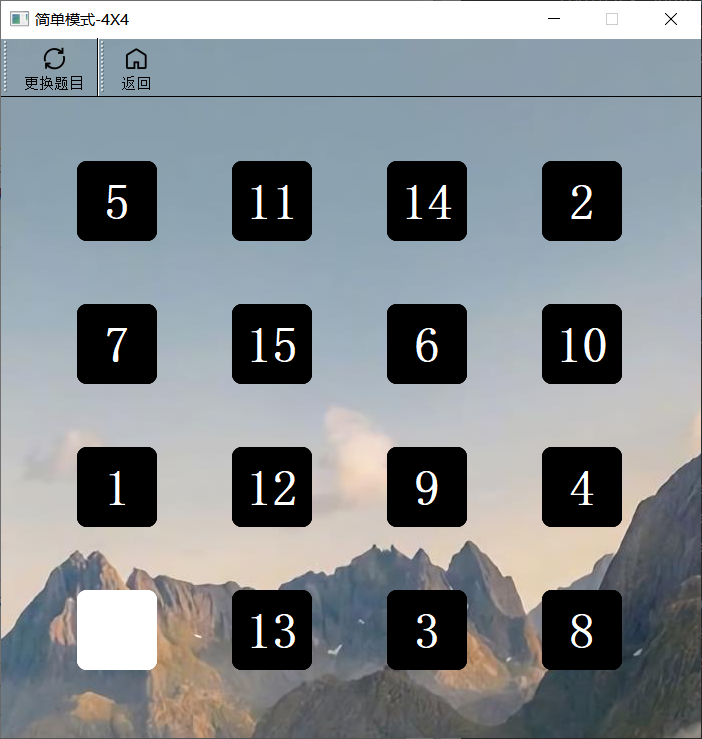
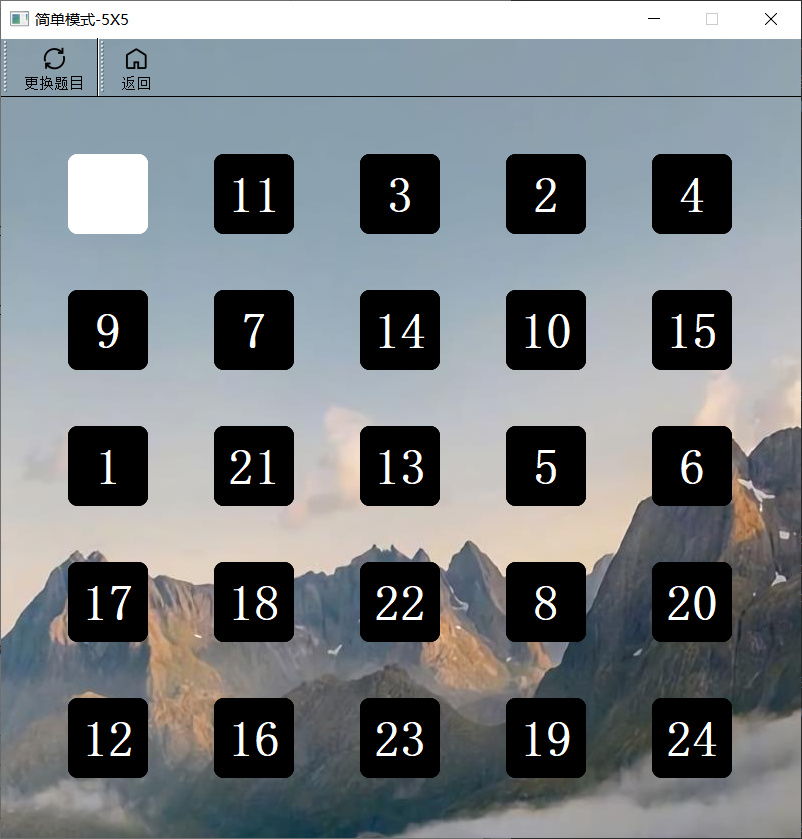
• 4X4和5X5模式，只要分别创建16个和25个数字方块放入网格布局中，相应的状态数组和判断游戏完成函数在3X3的基础上修改阶数即可。

通关挑战

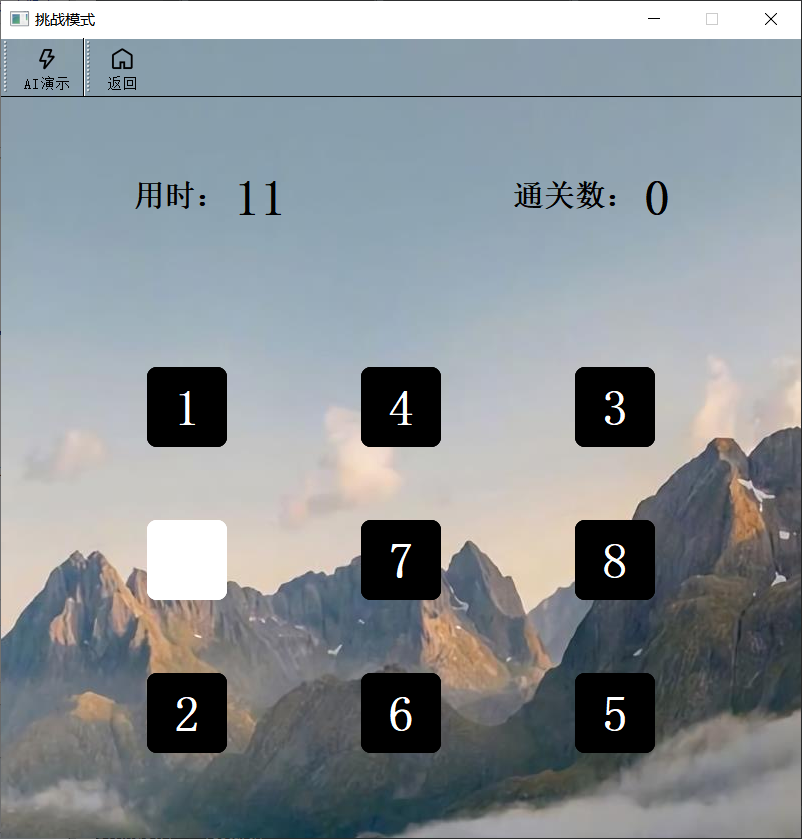
• 该模式要记录用户当前游戏用时和通关数，并在不同的通关数中，有不同的阶数模式。
• 记录用时，需要用到PyQt5的定时器QTimer，设置时间间隔为1秒，对数字（继承QLabel）进行加1。
• 同样地，记录通关数，当用户每完成一关游戏，相应的数字（继承QLabel）也加1。
• 该界面布局较为复杂，首先设置两个QFormLayout表单布局，分别为用时和对应的数字、通关数和对应的数字，将这两个表单布局放入QHBoxLayout水平布局中，将九个数字方块放入QGridLayout网格布局，再将水平布局和网格布局放入QVBoxLayout垂直布局，并使用setStretchFactor设置水平布局和网格布局大小为1：3。同样地，该窗口继承自QMainWindow，所以最后要同上文进行布局处理。
• 对于用户记录的处理，这里为将数据存入txt文件中，以供挑战记录窗口进行数据读取。这里将详细介绍如何实现用户记录排行榜：首先建立类为node，保存每条用户的记录，并使用优先队列，重写优先队列的判断函数，设置通关数越多，优先级越高，如果优先级相同，时间越短优先级越高。将每个node放入优先队列中。在每次用户完成挑战后，读取txt文件中的记录，并将记录通过字符串处理后，保存为node，放入优先队列，同时，将本次记录也保存为node放入优先队列，查看此次记录是否在优先队列的前十位，并将前十位重新转换为字符串，存入txt文件。

# 计时的实现
self.time_label = TimeLabel()
self.timer = QTimer()
self.timer.setInterval(1000)
self.timer.start()
# addtime为将QLabel数字加1
self.timer.timeout.connect(self.time_label.addtime)

# node类
class node(object):
    def __init__(self, date, num, time):
        self.date = date
        self.num = num
        self.time = time

    def __lt__(self, other):
        if self.num == other.num:
            return self.time < other.time
        else:
            return self.num > other.num

AI挑战

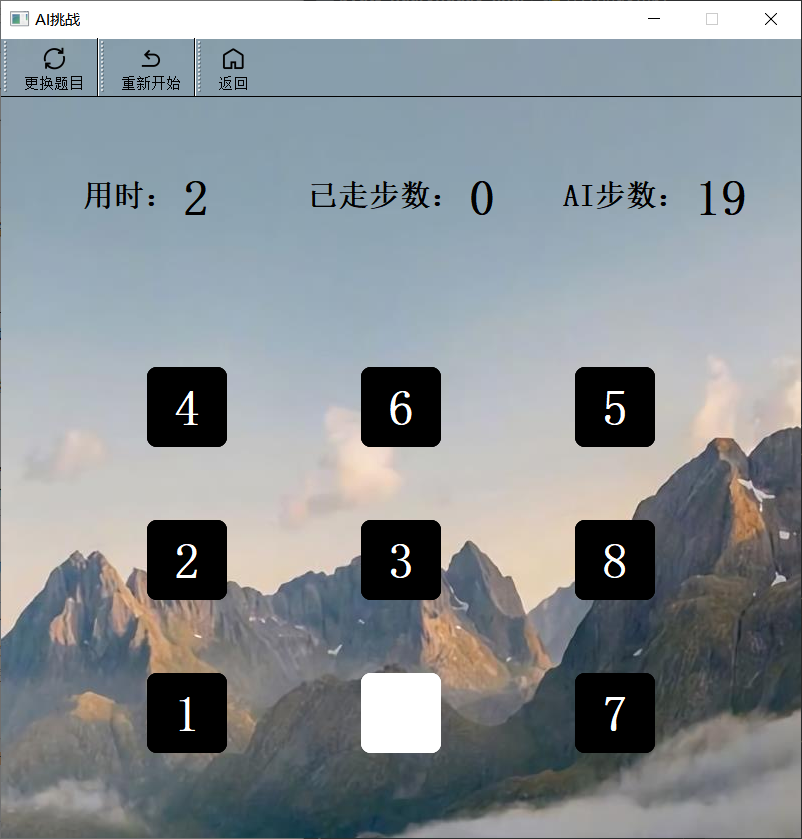
• 该模式用时同样需要使用QTimer，但对于已走步数，只能对合法的移动进行计数。
• 该模式给出AI完成此华容道需要走的步数，每当用户完成游戏后，均会给出是否打破记录的消息弹窗。
• 设置更换题目按钮，每次更换题目均需要初始化界面用时、已走步数为0，并重新执行A*算法，以得到最优解的步数。
• 考虑用户会在同一题上不断挑战自我，设置重新开始按钮，将此局重新开始，但并不更换题目，这就需要事先设置变量保存游戏状态数组和AI最优解。
• 该界面的布局、记录保存与通关挑战类似，不过多介绍。

# 将此局重新开始，而且一定需要使用deepcopy函数，后文会详细说明原因
def restart(self):
	self.block = copy.deepcopy(self.initblocks)
    self.zerorow = copy.deepcopy(self.initzerorow)
    self.zerocolumn = copy.deepcopy(self.initzerocolumn)
    self.updatePanel()
    self.toolbar3.setEnabled(True)
    self.toolbar2.setEnabled(True)

通关排名

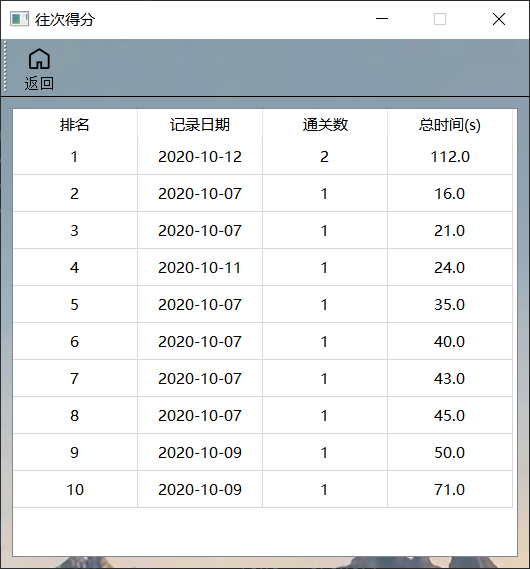
• 该界面记录通关挑战的游戏排名，展示数据为读取之前介绍的txt文件。
• 该界面布局为QTableWidget表格布局，设置禁止编辑和整行选择。

# 禁止编辑
tablewidget.setEditTriggers(QAbstractItemView.NoEditTriggers)
# 整行选择
tablewidget.setSelectionBehavior(QAbstractItemView.SelectRows)

AI排名

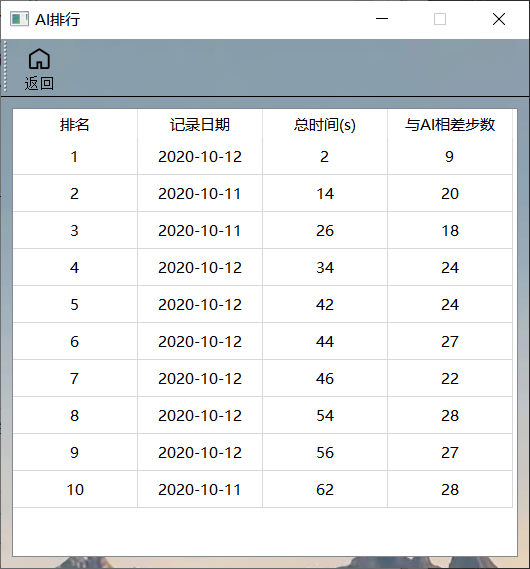
• 该界面与通关界面类似。

游戏规则

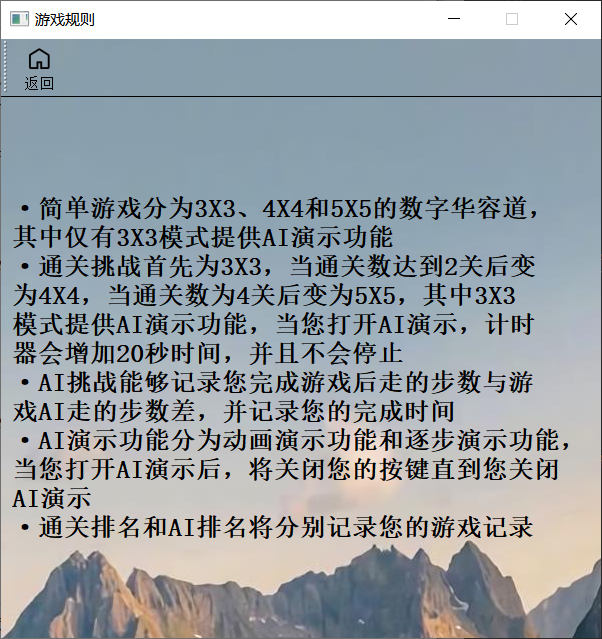
• 为了使界面更加美观，这里不使用QTextEdit，因为QTextEdit会覆盖整个背景图片，所以这里改为QLabel，并将游戏规则保存在txt文件中，方便修改。

AI界面

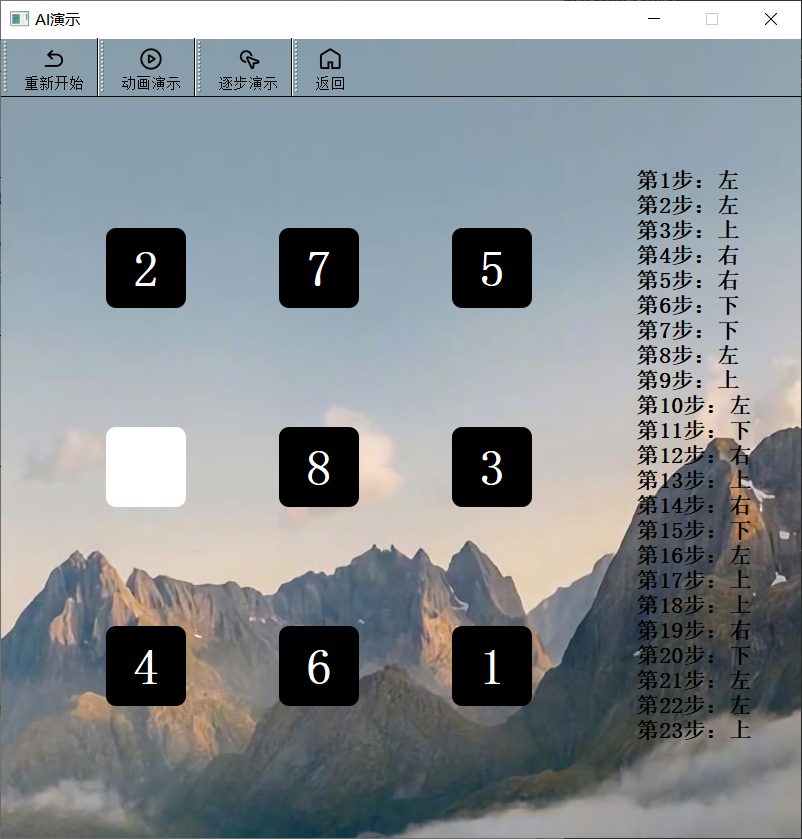
• 设置重新开始按钮，能够恢复AI演示后的局势，即需要设置变量存储刚开始传入的状态数组。
• 动画演示，使用QTimer定时器，在设置的时间间隔结束后，按照A*算法得出的移动序列，在每个时间段移动一步，并“刷新”界面。
• 逐步演示，在每一次点击按钮后，按照A*算法得出的移动序列，移动一步，并“刷新”界面。
• 移动序列，将A*算法得出的移动序列相对应地转换为上、下、左、右并以QLabel形式展示到界面。
• 当进行动画演示或逐步演示时，应该设置另外两个按钮不可点，以防止变量的数据混乱。

# 动画演示
def AIshow(self):
    self.timer = QTimer()
    self.timer.setInterval(100)
    self.timer.start()
    #时间间隔结束后执行walk函数
    self.timer.timeout.connect(self.walk)
    # 设置其他按钮是否可用，下同
    self.toolbar1.setEnabled(False)
    self.toolbar2.setEnabled(False)
    self.toolbar3.setEnabled(False)
    
# 按钮点击演示
def buttonshow(self):
    self.toolbar1.setEnabled(False)
    self.toolbar2.setEnabled(False)
    # self.walk_list为AI序列数组，self.walk_now为当前数组下标
    self.move(self.walk_list[self.walk_now])
    self.updatePanel()
    self.walk_now = self.walk_now + 1
    if self.walk_now == len(self.walk_list):
        self.walk_now = 0
        self.toolbar3.setEnabled(False)
        self.toolbar1.setEnabled(True)
        
# 实现自动移动
def walk(self):
    # move为移动函数
	self.move(self.walk_list[self.walk_now])
    self.updatePanel()
    self.walk_now = self.walk_now + 1
    # AI序列数组全部走完
    if self.walk_now == len(self.walk_list):
        self.timer.stop()
        self.walk_now = 0
        self.toolbar1.setEnabled(True)

A*算法

更具体的算法将在算法部分进行介绍，这里只介绍该GUi使用的A*算法的评价函数。

• 根据人工智能课上的A*算法结论：
• A*算法使可纳的，对于可解状态空间图，A*算法在有限步内终止并找到最优解。
• 在h(n)<=h*(n)的条件下，h(n)的值越大，携带的启发式信息越多，拓展的节点数越少，搜索效率越高。
• 对于八数码问题，有两种常见的h(n)选择，一种为h(n)为不在位数字块个数时，另一种为h(n)为每一个数字块于其目标位置之间距离的总和。容易发现，第二种h(n)的值比第一种h(n)的值要大，即携带的启发式信息更多，因此这里选择第二种h(n)，实际运行时，第二种h(n)运行速度更快。

#第一种h(n)
def setCost(self):
    c = 0
    for i in range(self.degree * self.degree):
        if self.num[i] != des1[i]:
            c = c + 1
     return c + self.step

#第二种h(n)
#位置对应表
pos = {
    '1': [1, 1],
    '2': [1, 2],
    '3': [1, 3],
    '4': [2, 1],
    '5': [2, 2],
    '6': [2, 3],
    '7': [3, 1],
    '8': [3, 2],
    '9': [3, 3]
}
def setCost(self):
    c = 0
    for i in range(self.degree * self.degree):
        if self.num[i] != des1[i]:
            temp = copy.deepcopy(self.num[i])
            if temp == 0:
                temp = 9
            #通过位置对应表，得到当前位置的x和y、目标位置的x和y
            x1 = pos[str(temp)][0]
            y1 = pos[str(temp)][1]
            x2 = pos[str(i + 1)][0]
            y2 = pos[str(i + 1)][1]
            #绝对值相减，得到距离
            res = abs(x1 - x2) + abs(y1 - y2)
            c = c + res
    return c + self.step

4）实现GUI时遇到的问题和解决+收获

编写GUI时，遇到的问题很多，这里介绍几个常见且重要的问题和解决思路

问题1：控件都正常放置，却不能正常显示

解决：

• 情况1：界面继承QMainWindow时，一定要将控件放入QWidget中，再放入self.setCentralWidget中，如图为QMainWindow的分布图。

  

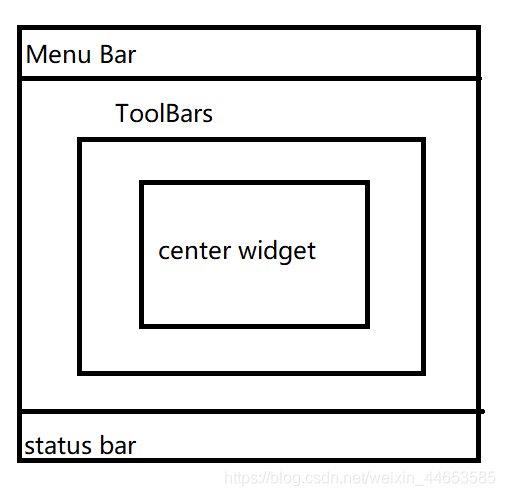
• 情况2：控件放入布局中错误，比如button在加入QVBoxLayout时，正常思维是将button放入一个widget中再放入QVBoxLayout，而这样做会产生错误，应该直接将button加入QVBoxLayout。同样地，QTextEdit也会出现上述的问题。

• 情况3：当控件定义为全局时，类似为self.button时，应该特别注意控件名的编写，避免手误，因为此时并不会报错，难发现错误。

问题2：AI演示完后，游戏界面的盘面会发生错误，数字块会被打乱或出现多个白块

解决：

• 在python中，如果两个变量互相赋值，那么这两个变量将会指向同一个内存地址。所以，当父窗口的变量作为参数传给子窗口后，子窗口再使用该参数进行运算，可能也会影响父窗口变量的值（或者有什么高深的原理，总之会出错）。因此，当游戏界面的状态数组和白块位置传给AI演示界面时，AI演示界面执行A*算法，改变了状态数组和白块位置，导致游戏界面盘面错误。这时，就需要调用python中的copy库的deepcopy函数，将所有父窗口和子窗口传递的变量进行拷贝赋值。（这个问题，其实在编写作业的AI算法时就遇到了，当初改了bug后没有重视，这次再次出现却耽误了很久。）

问题3：AI挑战和通过挑战多关后，定时器突然加快计时

解决：

• 如果使用的是QTimer的话，应该不会出现上述问题。产生上述问题，是由于当初并没有使用QTimer，而是使用了startTimer、killTimer和timeEvent。网上搜了一下，使用这三个结合的定时器，是多线程的，也就是说当游戏通过多次后，有多个线程的定时器同时改变计时数字，导出问题的出现。解决方法就是规规矩矩地使用QTimer。

收获：

• 实现了一个GUI这应该就是收获吧，但其实，最重要的还是真实地学到了些PyQt5和在结对编程中的经历。

5）游戏用户体验感调查结果

游戏在编写和测试时，邀请了数位同学进行测试，收集到了不少宝贵意见，并作出改进。

1.白块应该在1-9中随机选择还是固定为9？

• 多数同学认为应该固定为9，因为大家的正常思维还是习惯完成结果为右下角为白块。而且市场上的数字华容道APP也为固定9形式。

2.通关挑战有意思还是AI挑战有意思？

• 多数同学AI挑战有意思，因为AI挑战更有挑战自我，挑战AI的乐趣hhh，而通关挑战只能一股脑往下走，况且到后面5X5很难。但由于设计好了通关挑战，还是把这个板块也一起保留。

3.以什么形式来AI演示更直观？

• 动画演示、逐步演示、写出AI序列都是同学们的意见，因此将他们全部展示在AI演示界面中。

4.按键操控应该从白块的角度（白块想要往上就按上）还是以其他块的角度（白块下面的块想要往上就按上）？

• 几乎全部同学都认为应该选择第二种方式。

5.为什么4X4，5X5不设置AI演示？

• 4X4和5X5使用A*算法时，相较于3X3，拓展的节点数飞速增大，得到结果耗时非常长，影响游戏体验度。

Github代码签入记录

这是我的

荣胜的在这边：

异常处理

代码展示

emmm主代码部分实在想不到有什么问题orz，毕竟改完的代码跑的出正确答案= =

所以我们这次异常是针对测试数据这边写异常：

class NoSwapError(Exception):  # 针对不交换出解的样例

    def __init__(self):
        print("这是没强制交换前就能有解的样例欸！")

    def __str__(self, *args, **kwargs):
        return "再检查一下代码哦"


class SameMapError(Exception):  # 针对同一张图

    def __init__(self):
        print("一样的图，为什么还要移动呢？")

    def __str__(self, *args, **kwargs):
        return "再检查一下代码哦"


class SwapError(Exception):  # 针对交换后出解的样例

    def __init__(self):
        print("怎么没交换就出解了？")

    def __str__(self, *args, **kwargs):
        return "再检查一下代码哦"


class MoveError(Exception):# 针对不移动只交换就出解的样例
    def __init__(self):
        print("不用移动呢")

    def __str__(self):
        return "再检查一下代码哦"

这样既能检查我们的算法代码又能检查我们的测试数据代码，保证两边代码的正确性

具体应用（只展示部分）

    def test_noSwapMap(self):
        print("正在处理不需交换的样例……")
        operation = sample.SampleSolve(order2, origin2, swap2, step2)
        if len(operation) > step2:
            raise NoSwapError
            
    def test_answerOnlyBySwapMap2(self):
        print("正在处理只交换就出解的样例……")
        operation = sample.SampleSolve2(order7, origin7, swap7, step7)
        if operation[0] != ' ':
            raise MoveError

结对困难

遇到的问题和解决方案

我感觉我的表达能力有很多问题，很多时候线上交流荣胜无法get到我的意思，所以我们经常有问题的时候就会去玫瑰园或者是益和堂开个小会总结一下我们当前的问题，然后接着往下做修改

还有一点就是测试问题，因为我们两个人负责的东西不一样，所以可以起到两方互相当对方的测试人员的作用，也可以帮着改一些遇到的bug

收获

沟通应该说一直是我的一个问题吧，我身边同学跟我强调过很多次，甚至我辅导员都当面批评过= =，这次结对应该说对我的沟通能力有一些提高吧。

以前都没有碰过GUI相关的东西，写游戏也只是参照博客上的模板，这是我第一次和队友一起完善了一个游戏，感觉收获了很多。

评价你的队友

林荣胜同学是一个非常有团队意识的人，对这次结对作业非常的上心，gui部分基本是从零学起，能写出一个功能比较完整的华容道实在是不容易，算法部分也帮我想了很多东西，能和这样的人做结对编程是一件非常开心的事情。

学习进度条

第N周	新增代码（行）	累计代码（行）	本周学习耗时（小时）	累计学习耗时（小时）	重要成长
1	500	500	16	16	找各种算法以及完成原始A*算法C++向python的转译，完成图像识别和标号
2	200	700	16	32	完善算法（从传统八数码代码改向适用本问题的算法）以及改进算法
3	1500	2200	28	60	我完成单元测试部分代码以及改进算法，寻找更佳的估价函数
4	500	2700	32	92	根据ai大比拼题目结果改进算法，写博客

PSP表格

Personal Software Process Stages	预估耗时（分钟）	实际耗时（分钟）
Planning（计划）	538.4	480
Estimate（估计时间）	538.4	480
Development（开发）	5653.2	4320
Analysis（需求分析（包括学习新技术））	403.8	308
Design Spec（生成设计文档）	336.5	257
Design Review（设计复审）	269.2	205
Coding Standard（代码规范 ）	201.9	154
Design（具体设计）	673	514
Coding（具体编码）	2422.8	1851
Code Review（代码复审）	471.1	360
Test（测试（自我测试，修改代码，提交修改））	874.9	671
Reporting（报告）	538.4	600
Test Report（测试报告）	201.9	225
Size Measurement（计算工作量）	134.6	150
Postmortem & Process Improvement Plan（事后总结, 并提出过程改进计划）	201.9	225
Total（合计）	6730	5400

学习总结

1.这次结对编程真的下了挺多功夫的（主要还是没找到更高效的学习方法吧），感觉算法还是写的不够好（自己太菜了）。

2.通过结对编程可以看得出来在团队项目里沟通的地位肯定是更重要的，作为队长的我得加油了（泪目）。国庆happy了两天，深深的感到没有花足够时间打代码的罪恶（不是），主要团队作业和结对作业两边进度那段时间都没有很大的进展，第一次觉得事情还是得分配下去而不是自己一个人想清楚了再下发下去（这样进度好慢）。