B. OR in Matrix

B. OR in Matrix

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Let's define logical OR as an operation on two logical values (i. e. values that belong to the set {0, 1}) that is equal to 1 if either or both of the logical values is set to 1, otherwise it is 0. We can define logical OR of three or more logical values in the same manner:

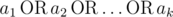where 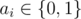is equal to 1 if some a_i = 1, otherwise it is equal to 0.

Nam has a matrix A consisting of m rows and n columns. The rows are numbered from 1 to m, columns are numbered from 1 to n. Element at row i (1 ≤ i ≤ m) and column j (1 ≤ j ≤ n) is denoted as A_ij. All elements of A are either 0 or 1. From matrix A, Nam creates another matrix B of the same size using formula:

.

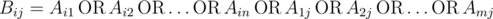(B_ij is OR of all elements in row i and column j of matrix A)

Nam gives you matrix B and challenges you to guess matrix A. Although Nam is smart, he could probably make a mistake while calculating matrix B, since size of A can be large.

Input

The first line contains two integer m and n (1 ≤ m, n ≤ 100), number of rows and number of columns of matrices respectively.

The next m lines each contain n integers separated by spaces describing rows of matrix B (each element of B is either 0 or 1).

Output

In the first line, print "NO" if Nam has made a mistake when calculating B, otherwise print "YES". If the first line is "YES", then also print m rows consisting of n integers representing matrix A that can produce given matrix B. If there are several solutions print any one.

Sample test(s)

Input

2 2
1 0
0 0

Output

NO

Input

2 3
1 1 1
1 1 1

Output

YES
1 1 1
1 1 1

Input

2 3
0 1 0
1 1 1

Output

YES
0 0 0
0 1 0

wa了几发才过、

#include <iostream>
#include <cstdio>
#include <cstring>
#include <string>
#include <algorithm>
#include <cstdlib>
using namespace std;

int a[110][110], b[110][110];

int main() {
	memset(a, 0, sizeof(a));
	memset(b, 0, sizeof(b));
	int m, n;
	cin >> m>> n;
	for (int i = 0; i<m; i++) {
		for (int j = 0; j<n; j++) {
			cin >> a[i][j];
			b[i][j] = 1;
		}
	}
	if (m == n && m == 1) {
		cout << "YES" << endl;
		cout << a[0][0] << endl;
		return 0;
	}
	int flag1 = 0, flag2 = 0, flag3 = 0, flag4 = 1;
	for (int i = 0; i<m; i++) {
		for (int j = 0; j<n; j++) {
			if (a[i][j] == 1) {
				flag4 = 0;
				flag1 = 0, flag2 = 0;
				for (int k = 0; k<n; k++) {
					if (a[i][k] != 1)
						flag1 ++ ;
				}
				for (int k = 0; k<m; k++) {
					if (a[k][j] != 1)
						flag2 ++ ;
				}
				if (flag1 == 0 && flag2 == 0)
					flag3 ++ ;
				else if (flag1>0 && flag2>0) {
					cout << "NO"<< endl;
					return 0;
				}
			}
		}
	}
	if (flag4 == 1) {
		cout << "YES" << endl;
		for (int i = 0; i<m; i++) {
			for (int j = 0; j<n-1; j++) {
				cout << a[i][j] << " ";
			}
			cout << a[i][n-1] << endl;
		}
		cout << endl;
		return 0;
	}
	if (flag3 > 0) {
		cout << "YES"<< endl;
		for (int i = 0; i<m; i++) {
			for (int j = 0; j<n; j++) {
				if (a[i][j] == 0) {
					for (int k = 0; k<n; k++) 
						b[i][k] = 0;
					for (int k = 0; k<m; k++)
						b[k][j] = 0;
				}
			}
		}
		for (int i = 0; i<m; i++) {
			for (int j = 0; j<n-1; j++) {
				cout << b[i][j] << " ";
			}
			cout << b[i][n-1] << endl;
		} 
		cout << endl;
	}
	else {
		cout << "NO" << endl;
	}
	
	return 0;
}