1,球性插值
代码转载自:http://blog.csdn.net/ZFSR05255134/article/details/51075668
根据文章介绍本人对球面插值理解如图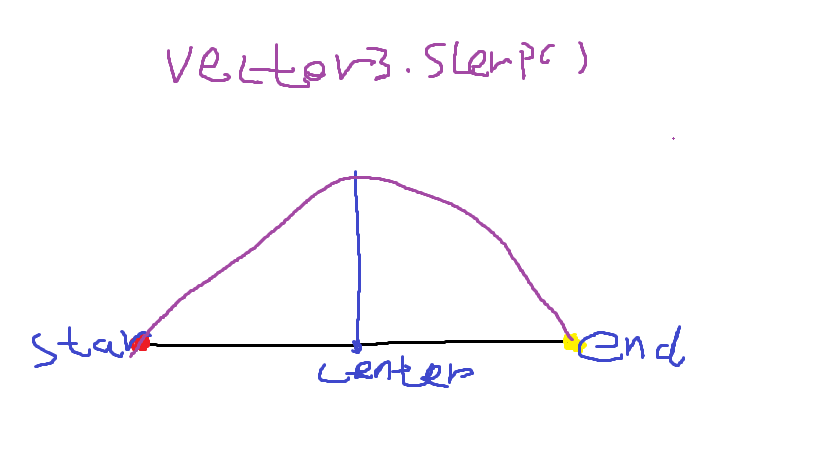
using UnityEngine; using System.Collections; /// <summary> /// 在日出和日落之间动画弧线 /// 网上看到有人对Vector3.Slerp()的详解,但是经过962f之力将他的思路看明白。 /// 受到启发,就有了自己对Vector3.Slerp()的理解。tt2()函数、tt3()函数是自己的写的,tt4()是别人的。 /// tt2()函数球形插值 /// tt3()函数利用球形插值绘制类似抛物线。 /// </summary> public class Vector3_Slerp_2 : MonoBehaviour { /// <summary> /// 日出 /// </summary> public Transform sunrise; /// <summary> /// 日落 /// </summary> public Transform sunset; /// <summary> /// 计算中间点的一个因素 /// </summary> public float m_centerFac = 0.5f; /// <summary> /// 插值中心点的影响因素 /// </summary> public float m_moveTowardsValue = 1f; /// <summary> /// 插值的个数 /// </summary> public int m_lineNum = 30; private Vector3 mStart = Vector3.zero; private Vector3 mEnd = Vector3.zero; void Update() { //tt2(); tt3(); //tt4(); } /// <summary> /// 官方用例 /// </summary> private void tt1() { //弧线的中心 Vector3 center = (sunrise.position + sunset.position) * 0.5f; //向下移动中心,垂直于弧线 center -= new Vector3(0, 1, 0); //相对于中心在弧线上插值 Vector3 riseRelCenter = sunrise.position - center; Vector3 setRelCenter = sunset.position - center; transform.position = Vector3.Slerp(riseRelCenter, setRelCenter, Time.time); transform.position += center; } /// <summary> /// 球面插值 /// 自己的理解 /// 只在垂直平面上做球面插值。 /// </summary> private void tt2() { mStart = sunrise.position; mEnd = sunset.position; /// 绘制世界坐标系 Debug.DrawLine(new Vector3(-100, 0, 0), new Vector3(100, 0, 0), Color.green); Debug.DrawLine(new Vector3(0, -100, 0), new Vector3(0, 100, 0), Color.green); Debug.DrawLine(new Vector3(0, 0, -100), new Vector3(0, 0, 100), Color.green); /// 求出起始点与终点的中心点 Vector3 center = (mStart + mEnd) * m_centerFac; //////////////////////////////////// /// 1. center、mStart、mEnd 构成一个平面A //////////////////////////////////// Debug.DrawLine(new Vector3(center.x, 0f, center.z), center, Color.white); /// 绘制一个三角形 Debug.DrawLine(new Vector3(center.x, 0f, center.z), mStart, Color.white); Debug.DrawLine(new Vector3(center.x, 0f, center.z), mEnd, Color.white); Debug.DrawLine(mStart, mEnd, Color.white); Vector3 normal = mEnd - mStart; ///只在垂直平面上做球面插值。 Vector3 tangent = new Vector3(center.x, 0f, center.z) - center; /// 两个坐标轴的正交化。 Vector3.OrthoNormalize(ref normal, ref tangent); float moveTowardsValue = (mEnd - mStart).magnitude * m_moveTowardsValue; Vector3 center2 = center + tangent * moveTowardsValue; //////////////////////////////////// /// 2. 两个坐标轴的正交化后 center2、mStart、mEnd 构成一个平面B, /// 3. 平面B与平面A是同一平面。 //////////////////////////////////// Debug.DrawLine(center2, mStart, Color.blue); Debug.DrawLine(center2, mEnd, Color.blue); Debug.Log(string.Format("{0} : {1}", Vector3.Distance(center2, mStart), Vector3.Distance(center2, mEnd))); for (int i = 1; i < m_lineNum; ++i) { Vector3 drawVec = Vector3.Slerp(mEnd - center2, mStart - center2, 1f / m_lineNum * i); drawVec += center2; Debug.DrawLine(center2, drawVec, Color.yellow); } /// 绘制起始点与终点的中心点到计算出的插值的中心点 Debug.DrawLine(center, center2, Color.black); } /// <summary> /// 利用球面插值模拟抛物线 /// 自己的理解 /// </summary> private void tt3() { mStart = sunrise.position; mEnd = sunset.position; /// 绘制世界坐标系 Debug.DrawLine(new Vector3(-100, 0, 0), new Vector3(100, 0, 0), Color.green); Debug.DrawLine(new Vector3(0, -100, 0), new Vector3(0, 100, 0), Color.green); Debug.DrawLine(new Vector3(0, 0, -100), new Vector3(0, 0, 100), Color.green); /// 求出起始点与终点的中心点 Vector3 center = mEnd + (mStart - mEnd) * m_centerFac; //////////////////////////////////// /// 1. center、mStart、mEnd 构成一个平面A //////////////////////////////////// Debug.DrawLine(new Vector3(center.x, mEnd.y, center.z), center, Color.white); /// 绘制一个三角形 Debug.DrawLine(new Vector3(center.x, mEnd.y, center.z), mStart, Color.white); Debug.DrawLine(new Vector3(center.x, mEnd.y, center.z), mEnd, Color.white); Debug.DrawLine(mStart, mEnd, Color.white); Vector3 normal = mStart - mEnd; ///只在垂直平面上做球面插值。 Vector3 tangent = new Vector3(center.x, mEnd.y, center.z) - center; /// 两个坐标轴的正交化。 Vector3.OrthoNormalize(ref normal, ref tangent); float moveTowardsValue = (mEnd - mStart).magnitude * m_moveTowardsValue; //Vector3 center2 = center + tangent * moveTowardsValue; Vector3 center2 = center - Vector3.up * moveTowardsValue; //////////////////////////////////// /// 2. 两个坐标轴的正交化后 center2、mStart、mEnd 构成一个平面B, /// 3. 平面B与平面A是同一平面。 //////////////////////////////////// Debug.DrawLine(center2, mStart, Color.blue); Debug.DrawLine(center2, mEnd, Color.blue); Debug.Log(string.Format("{0}:{1} -- {2}:{3}", Vector3.Distance(center2, mStart), Vector3.Distance(center2, mEnd), Vector3.Distance(mEnd, mStart), Vector3.Distance(center2, center))); for (int i = 1; i < m_lineNum; ++i) { Vector3 drawVec = Vector3.Slerp(mEnd - center2, mStart - center2, 1f / m_lineNum * i); drawVec += center2; Debug.DrawLine(center2, drawVec, Color.yellow); } /// 绘制起始点与终点的中心点到计算出的插值的中心点 Debug.DrawLine(center, center2, Color.black); } /// <summary> /// 球面插值 /// http://www.manew.com/thread-43314-1-1.html 文章用例 /// </summary> private void tt4() { mStart = sunrise.position; mEnd = sunset.position; Debug.DrawLine(new Vector3(-100, 0, 0), new Vector3(100, 0, 0), Color.green); Debug.DrawLine(new Vector3(0, -100, 0), new Vector3(0, 100, 0), Color.green); Debug.DrawLine(new Vector3(0, 0, -100), new Vector3(0, 0, 100), Color.green); Debug.DrawLine(Vector3.zero, mStart, Color.white); Debug.DrawLine(Vector3.zero, mEnd, Color.white); Debug.DrawLine(mStart, mEnd, Color.white); /// 求出起始点与终点的中心点 Vector3 centor = (mStart + mEnd) * 0.5f; Debug.DrawLine(Vector3.zero, centor, Color.blue); Vector3 centorProject = Vector3.Project(centor, mStart - mEnd); // 中心点在两点之间的投影 centor = Vector3.MoveTowards(centor, centorProject, m_moveTowardsValue); // 沿着投影方向移动移动距离(距离越大弧度越小) Debug.DrawLine(centor, mStart, Color.blue); Debug.DrawLine(centor, mEnd, Color.blue); Debug.Log(string.Format("{0} : {1}", Vector3.Distance(centor, mStart), Vector3.Distance(centor, mEnd))); for (int i = 1; i < m_lineNum; ++i) { Vector3 drawVec = Vector3.Slerp(mEnd - centor, mStart - centor, 1f / m_lineNum * i); drawVec += centor; Debug.DrawLine(centor, drawVec, Color.yellow); //Debug.DrawLine(centor, drawVec, 5 == i ? Color.blue : Color.yellow); } } }
其他关于球形插值的参考文章:http://www.ituring.com.cn/article/120745
基本语法 public static Vector3 Slerp(Vector3 from, Vector3 to, float t);
其中参数from为插值起始点坐标,参数to为插值结束点坐标,参数t为插值系数。
功能说明 此方法用于返回从参数from点到参数to点的球形插值向量。例如,设现有Vector3实例A和B(如图14-15所示),则执行如下程序代码后
Vector3 C=Vector3. Slerp (from, to, t);
当t≤0时,向量C=A;
当t≥1时,向量C=B;
当t从0增加到1时,向量C会从起始点A绕着A×B(即向量A和B的叉乘)的方向匀速移动到向量B,此处的匀速是指角度旋转的匀速,即向量C与B的夹角k=e*(1t),如图14-15所示,这样便可确定向量C的方向。而向量C的模长计算公式则为:
;
这样便可以确定向量C了。
当向量A和B中某个分量的值都为0时,比如它们的y轴分量都为0,即ay=by=0时,则A将绕着y轴在xz平面匀速旋转向B移动,并且在移动过程中C.y的值始终为0。
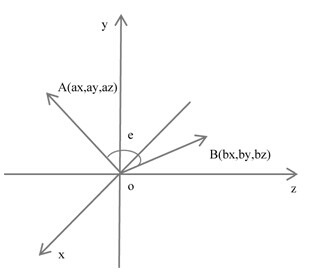
图14-15 Slerp球形插值
实例演示 下面通过实例演示方法Slerp的使用。
using UnityEngine;
using System.Collections;
public class Slerp_ts : MonoBehaviour {
public Transform from_T, to_T;
Vector3 from_v, to_v;
Vector3 slerps = Vector3.zero;
float speed = 0.1f;
void Start () {
//初始化起始位置
from_v = from_T.position;
to_v = to_T.position;
}
void Update () {
//在1/speed时间内slerps从from_v移动到to_v
slerps = Vector3.Slerp(from_v,to_v,Time.time*speed);
//绘制从原点到slerps的红线,并保留100秒以便观察
//运行时只能在scene视图中查看
Debug.DrawLine(Vector3.zero,slerps,Color.red,100.0f);
}
}
在这段代码中,首先声明了3个Vector3变量from_v、to_v和slerps,并在Start方法中对其初始化,然后在方法Update中将方法Vector3.Slerp的返回值赋给slerps,最后绘制一条从世界坐标系原点到slerps的直线。请自行运行程序,查看slerps点的移动轨迹,运行时请在Scene视图而非Game视图中查看,
图14-16是一张运行时截图及注释。
