题目描述
司令部的将军们打算在 (N*M) 的网格地图上部署他们的炮兵部队。一个(N*M) 的地图由N行M列组成,地图的每一格可能是山地(用“(H)” 表示),也可能是平原(用“(P)”表示),如下图。在每一格平原地形上最多可以布置一支炮兵部队(山地上不能够部署炮兵部队);一支炮兵部队在地图上的攻击范围如图中黑色区域所示:
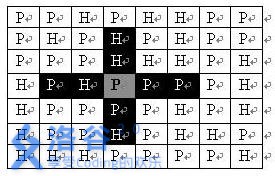
如果在地图中的灰色所标识的平原上部署一支炮兵部队,则图中的黑色的网格表示它能够攻击到的区域:沿横向左右各两格,沿纵向上下各两格。图上其它白色网格均攻击不到。从图上可见炮兵的攻击范围不受地形的影响。 现在,将军们规划如何部署炮兵部队,在防止误伤的前提下(保证任何两支炮兵部队之间不能互相攻击,即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内),在整个地图区域内最多能够摆放多少我军的炮兵部队。
输入格式
第一行包含两个由空格分割开的正整数,分别表示 (N) 和 (M) ;
接下来的 (N) 行,每一行含有连续的 (M) 个字符(‘ (P) ’或者‘ (H) ’),中间没有空格。按顺序表示地图中每一行的数据。(N≤100);(M≤10)。
输出格式
仅一行,包含一个整数 (K),表示最多能摆放的炮兵部队的数量。
输入输出样例
输入 #1复制
5 4
PHPP
PPHH
PPPP
PHPP
PHHP
输出 #1复制
6
题解
这是一个状压 (dp) ,对于一个位置 (p) ,选择在这个位置部署一支炮兵部队,需要考虑前两行状态和前两个位置没有部署炮兵部队,
对于同一行有没有部署炮兵的情况可以通过直接枚举每一行的状态来进行演变,
枚举的范围为 (0-(1<<m)) ,当这个状态二进制为 (1) 时,即是在这个位置部署炮兵部队,否则即为没有,
这样的话,前两个位置没有部署炮兵部队的问题就解决了,
对于前两行的状态而言的,需要任何两个的 (&) 值为 (0) ,
解决的方式是通过创建一个数组,同时存储当前状态和它的前一个状态,
保证 (&) 值为 (0)
注意:
- 如果按照我的方法而言内存限制因素比较大,需要经过滑动状态来进行保存,因为一个状态他只会取决于它的前一个状态,所以滑动窗口的最小长度为 (2)
- 也可能会 (TLE) ,需要经过提前预处理一下,每一行能够部署炮兵的状态以及每一个二进制对应的位置
代码
#include <vector>
#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
const int maxn = 1030;
int dp[3][maxn][maxn];
int cnt[maxn];
char s[101][11];
vector<int>v[101];
inline bool check(int n,int m,int x){
for(int i=0;i<m;++i){
if(s[n][i]=='H'&&((x>>i)&1))
return false;
}
int pos=-3;
for(int i=0;i<m;++i){
if((x>>i)&1){
if((i-pos)<3)return false;
pos=i;
}
}
return true;
}
inline short int ret(int n){
int res=0;
while(n){
if(n&1)res++;
n>>=1;
}
return res;
}
inline void init(int n){
for(int i=0;i<n;++i){
cnt[i]=ret(i);
}
}
int main(){
int n,m;
init(1<<10);
memset(dp,0,sizeof(dp));
scanf("%d%d",&n,&m);
for(int i=0;i<n;++i){
scanf("%s",s[i]);
for(int j=0;j<(1<<m);++j){
if(check(i,m,j))v[i].push_back(j);
}
}
for(int i=0;i<n;++i){
for(int j=0;j<(int)v[i].size();++j){
if(i){
if(i==1){
for(int x=0;x<(int)v[i-1].size();++x){
if((v[i][j]&v[i-1][x])==0){
dp[i%3][v[i][j]][v[i-1][x]]=max(dp[i%3][v[i][j]][v[i-1][x]],dp[(i-1)%3][v[i-1][x]][0]+cnt[v[i][j]]);
}
}
}
else{
for(int x=0;x<(int)v[i-1].size();++x){
if((v[i][j]&v[i-1][x])==0)
for(int y=0;y<(int)v[i-2].size();++y){
if((v[i-2][y]&v[i][j])==0&&(v[i-1][x]&v[i-2][y])==0&&(v[i][j]&(v[i-1][x]|v[i-2][y]))==0){
dp[i%3][v[i][j]][v[i-1][x]]=max(dp[i%3][v[i][j]][v[i-1][x]],dp[(i-1)%3][v[i-1][x]][v[i-2][y]]+cnt[v[i][j]]);
}
}
}
}
}
else {
if(i==0){
dp[i][v[i][j]][0]=cnt[v[i][j]];
}
}
}
}
int maxx=0;
for(int i=0;i<3;++i){
for(int x=0;x<(1<<m);++x){
for(int y=0;y<(1<<m);++y){
maxx=max(maxx,dp[i][x][y]);
}
}
}
printf("%d
",maxx);
return 0;
}